Types of Polynomials
Polynomials can be classified based on their degree and number of terms. The degree of a polynomial is the highest power of its variable, and it determines the shape and behaviour of the polynomial's graph. An example of a polynomial is x2+2x-3. This polynomial has 3 terms in it and its degree is 2 since the term with the highest power of 'x' is 'x2'.
Some common types of polynomials include linear polynomials, quadratic polynomials, cubic polynomials, and higher-degree polynomials. Let us see what are different types of polynomials along with examples.
Introduction to Polynomials
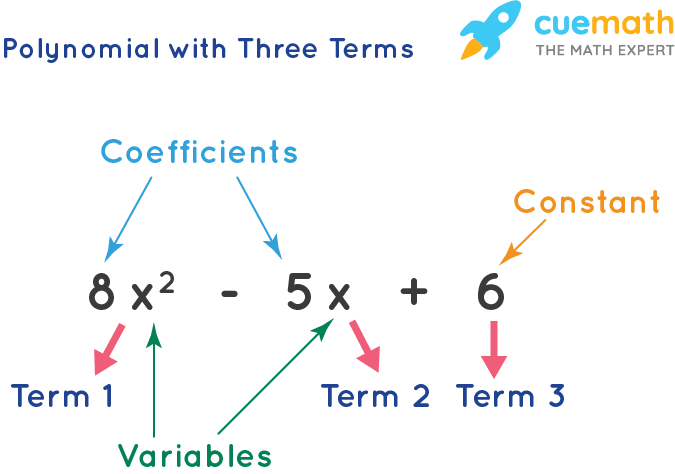
Polynomials are algebraic expressions in which the variables have only non-negative integer powers. For example, 5x2 - x + 1 is a polynomial. The algebraic expression 3x3 + 4x + 5/x + 6x3/2 is not a polynomial, since one of the powers of 'x' is a fraction and the other is negative. Polynomials are expressions with one or more terms having a non-zero coefficient. The terms of polynomials comprise variables, exponents, and constants. The first term of the polynomial in standard form is called the "leading term".
A standard polynomial is one where the highest degree is the first term, and the subsequent terms are arranged in descending order of the powers or the exponents of the variables followed by constant values. The number multiplied by a variable is called the "coefficient". The number without any variable is called a "constant".
What are Types of Polynomials?
The polynomials can be classified in two ways: based on degree and based on the number of terms.
- The types of polynomials based on degree: zero polynomial, linear, quadratic, and cubic polynomials.
- The types of polynomials based on the number of terms: monomials, binomials, trinomials, etc.

Let us see each of these types in the upcoming sections in detail.
Types of Polynomials Based on Degree
The power of the leading term or the highest power of the variable is called the degree of the polynomial. This is obtained by arranging the terms of polynomials in the descending order of their powers. Based on the degree of the polynomial, they can be classified into 4 major types. They are,
Look at the table given below to understand the meaning of the types of polynomials with examples.
| Type of Polynomial | Meaning | Examples |
|---|---|---|
| Zero or constant polynomial | Polynomials with 0 degree. | 3 or 3x0 |
| Linear polynomial | Polynomials with 1 as the degree. | x + y - 4, 5m + 7n, 2p |
| Quadratic polynomial | Polynomials with 2 as the degree. | 8x2 + 7y - 9, m2 + mn - 6 |
| Cubic polynomial | Polynomials with 3 as the degree. |
3x3, p3 + pq + 7 |
Types of Polynomials Based on Terms
There are different types of polynomials with respect to their number of terms. There are polynomials with one term, two terms, three terms, and even more. Based on the number of terms, polynomials are classified as:
- Monomials: A monomial is a polynomial expression that contains only one term. For example 4t, 21x, 2y, 9pq. Furthermore, 2x + 5x + 10x is a monomial because these are like terms added together that result in 17x, which is a single term.
- Binomials: A binomial is a polynomial with two, unlike terms. For example, 3x + 4x2 is a binomial as it contains two unlike terms, that is, 3x and 4x2. and 10pq + 13p2.
- Trinomials: A trinomial is a polynomial with three, unlike terms. For example, 3x + 5x2 – 6x3 and 12pq + 4x2 – 10.
We can also have more than 3 terms in a polynomial expression. Polynomials that have 4 unlike terms are called four-term polynomials. Similarly, polynomials with 5 terms are called five-term polynomials, and so on.
Special Types of Polynomials
Apart from the types of polynomials, that we have learned in the previous sections, there are some special types of polynomials.
- Monic polynomial: a polynomial whose leading coefficient is 1. Example: x3 + 3x + 3.
- Irreducible polynomial: a polynomial that cannot be factored into lower-degree polynomials over a given field. Example: x2 + 2 is irreducible over the set of real numbers.
- Homogeneous polynomial: a polynomial where all the terms have the same degree. Example: x2 + xy + y2.
Important Notes on Types of Polynomials:
- Two terms of polynomials are separated by the addition or subtraction sign. Multiplication and division operators are not used to create more terms in a polynomial. For example, 3xy is considered as 3 × x × y, is a monomial, whereas 3x+y is a binomial.
- Based on the terms in a polynomial, it can be classified into the following 3 types: monomial, binomial, trinomial.
- Based on the degree of a polynomial, it can be classified into 4 types: zero polynomial, linear polynomial, quadratic polynomial, cubic polynomial.
- Polynomials should have a whole number as the degree. Expressions with negative exponents are not polynomials. For example, x-2 is not a polynomial.
- Polynomials do not have variables in their denominator. For example, 2/(x+2) is not a polynomial.
☛ Related Topics:
Solved Examples on Types of Polynomials
-
Example 1: From the list of polynomials find the types of polynomials that have a degree of 2 and above 2 and classify them accordingly.
i) x + 7
ii) x2 + 3x + 2
iii) z3 + 2xz + 4Solution:
The given polynomials are in the standard form. The degree of a polynomial is the greatest exponent.
(i) The degree of the polynomial x + 7 is 1, so it is linear.
(ii) In the polynomial, x2 + 3x + 2 the degree is 2, and so it is called a quadratic polynomial.
(iii) In z3 + 2xz + 4, the polynomial has a degree of 3. It is called a cubic polynomial.
Answer: (ii) and (iii) have degrees 2 or greater than 2. (ii) is a quadratic polynomial and (iii) is a cubic polynomial. -
Example 2: Mention the names of polynomials.
i) n3 + 6
ii) 5x2 + 2xy + 1
iii) p - 82
iv) 2p2 + q - 11
v) 34Solution:
We classify the given polynomials with respect to their degree and the number of terms.
Polynomial Type (based on degree) Type (based on number of terms) n3 + 6 Cubic (degree = 3) Binomial (2 terms) 5x2 + 2xy + 1 Quadratic (degree = 2) Trinomial (3 terms) p - 82 Linear (degree = 1) Binomial (2 terms) 2p2 + q - 11 Quadratic (degree = 2) Trinomial (3 terms) 34 Constant (degree = 0) Monomial (1 term) Answer: The types of polynomials are mentioned in the above table.
-
Example 3: What type of polynomial is 3x3 - 5x2 + 3x + 2?
Solution:
The given polynomial has 4 terms in it and hence it has no specific name in the types of polynomials. It is just called a polynomial.
In specific, it is a cubic polynomial as its degree is 3.
Answer: Cubic polynomial.

Practice Questions on Types of Polynomials
FAQs on Types of Polynomials
What are Different Types of Polynomials?
A polynomial is an expression that is made up of variables and constants. Polynomials are categorized based on their degree and the number of terms. Here is the table that shows how polynomials are classified into different types.
| Polynomials Based on Degree | Polynomials Based on Number of Terms |
|---|---|
| Constant (degree = 0) | Monomial (1 term) |
| Linear (degree 1) | Binomial (2 terms) |
| Quadratic (degree 2) | Trinomial (3 terms) |
| Cubic (degree 3) | Polynomial (more than 3 terms) |
| Quartic (or) Biquaadratic (degree 4) | |
| Quintic (degree 5) | |
| and so on ... |
What are the Types of Polynomials Based on the Number of Terms?
Polynomials are categorized according to the number of terms as follows. They are,
- Monomials: It is a polynomial with one term. Examples: 3x, 4z, -7p, etc,.
- Binomials: It is a polynomial with two unlike terms. Examples: 3a - 5b, 7y + 10 z, etc.
- Trinomials: It is a polynomial with three unlike terms. Examples: x + y + 3z, a2 + 5b + 2, etc.
In a polynomial, there should not be any negative number as the exponent of the variable. The variable should not be in the denominator of the polynomial that is in fractional form.
pqr is What Type of Polynomial?
pqr is just one term because there is no addition/subtraction being happened here. Thus, pqr is a monomial.
What are the Types of Polynomials Based on Degree?
Polynomials can be classified on the basis of their degree as follows. They are,
- Zero polynomial: The degree of zero polynomials is 0. For example, 2 or 2y0.
- Linear polynomial: The degree of linear polynomials is 1. For example, p + q - 2.
- Quadratic polynomial: The degree of quadratic polynomials is 2. For example, x2 + 3x + 3.
- Cubic polynomial: The degree of cubic polynomials is 3. For example, 5x3 - 1.
What Type of Polynomial is a Polynomial with 5 Terms?
Polynomials with 5 terms are known as five-term polynomials (there is no specific name). For example, 3x3-xy+y2+6x2-8.
What is a Polynomial with Degree 4 Called?
Polynomials with degree 4 are known as quartic (or) bi-quadratic polynomials. For example, x4+3x3-2x+5.
visual curriculum