Calculus
Calculus is one of the most important branches of mathematics that deals with rate of change and motion. The two major concepts that calculus is based on are derivatives and integrals.
- The derivative of a function is the measure of the rate of change of a function. It gives an explanation of the function at a specific point.
- The integral is the measure of the area under the curve of the function. It accumulates the discrete values of a function over a range of values.
Calculus is also referred to as infinitesimal calculus or “the calculus of infinitesimals”. Infinitesimal numbers are quantities that have a value nearly equal to zero, but not exactly zero. Generally, classical calculus is the study of continuous changes of functions.
| 1. | What is Calculus? |
| 2. | Calculus Topics |
| 3. | Functions |
| 4. | Differential Calculus |
| 5. | Integral Calculus |
| 6. | Calculus Formula |
| 7. | Applications of Calculus |
| 8. | FAQs on Calculus |
What is Calculus?
Calculus focuses on some important topics covered in math such as differentiation, integration, limits, functions, and so on. Calculus, a branch of mathematics, deals with the study of the rate of change and it was developed by Newton and Leibniz.
Calculus Definition: Calculus in mathematics is generally used in mathematical models to obtain optimal solutions and thus helps in understanding the changes between the values related by a function. Calculus is broadly classified into two different sections:
- Differential Calculus
- Integral Calculus

Both differential calculus and integral calculus serve as a foundation for the higher branch of Mathematics known as “Analysis”, dealing with the impact of a slight change in the dependent variable, as it leads to zero, on the function.
Calculus Topics
Based on the complexity of the concepts covered under calculus, we classify the topics under different categories as listed below,
- Precalculus
- Calculus 1
- Calculus 2
Precalculus
Precalculus in mathematics is a course that includes trigonometry and algebra designed to prepare students for the study of calculus. In precalculus, we focus on the study of advanced mathematical concepts including functions and quantitative reasoning. Some important topics covered under precalculus are,
Calculus 1
Calculus 1 covered the topics mainly focusing on differential calculus and the related concepts like limits and continuity. Some of the topics covered under calculus 1 are,
Calculus 2
Calculus 2 focuses on the mathematical study of change first introduced during the curriculum of Calculus 1. Some of the important topics under Calculus 2 are,
- Differential Equations
- Sequence and Series
- Application of Integrals
- Trapezoidal Rule and Simpsons Rule
Functions
Functions in calculus represent the relationship between two variables, which are the independent variable and the dependent variable. Let’s consider the following diagram.

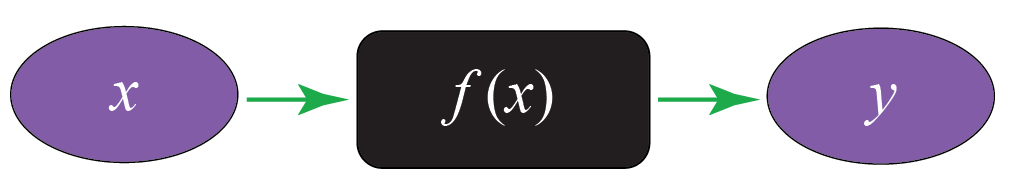
There is an INPUT, a function, and an OUTPUT. For example, suppose we want to make a pizza. We would need the following basic ingredients.
- Pizza Base
- Pizza Sauce
- Cheese
- Seasoning
The above real-life example can be represented in the form of a function as explained below,

Let’s take another example
Suppose that: y = x2
| Value of x | Value of y |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 9 | 81 |
| 11 | 121 |
Using the diagram given above, we get:

We can see that the value of y depends on the value of x. We can conclude that, in calculus,
- INPUT (x) is independent of the OUTPUT (y)
- OUTPUT depends on the INPUT
- f(x) is responsible for the transformation of the INPUT to the OUTPUT and is called a "function"
Differential Calculus
Differential calculus focuses on solving the problem of finding the rate of change of a function with respect to the other variables. To find the optimal solution, derivatives are used to calculate the maxima and minima values of a function. Differential helps in the study of the limit of a quotient, dealing with variables such as x and y, functions f(x), and the corresponding changes in the variables x and y. The notations dy and dx are known as differentials. The process used to find the derivatives is called differentiation. The derivative of a function, y with respect to variable x, is represented by dy/dx or f’(x).
Limits
Limit helps in calculating the degree of closeness to any value or the approaching term. A limit is normally expressed using the limit formula as,
limx→cf(x) = A
This expression is read as “the limit of f of x as x approaches c equals A”.
Derivatives
Derivatives represent the instantaneous rate of change of a quantity with respect to the other. The derivative of a function is represented as:
limx→h[f(x + h) − f(x)]/h = A
Continuity
A function f(x) is said to be continuous at a particular point x = a, if the following three conditions are satisfied –
- f(a) is defined
- limx→af(x) exists
- limx→af(x) = f(a)
Continuity and Differentiability
A function is always continuous if it is differentiable at any point, whereas the vice-versa for this condition is not always true.
Integral Calculus
Integral calculus is the study of integrals and the properties associated to them. It is helpful in:
- calculating f from f’ (i.e. from its derivative).
- calculating the area under a curve for any function.
Integration
Integration is the reverse process of differentiation. As differentiation can be understood as dividing a part into many small parts, integration can be said as a collection of small parts in order to form a whole. It is generally used for calculating areas.
Indefinite Integral
An indefinite integral does not have a specific boundary, i.e. no upper and lower limit is defined. Thus the integration value is always accompanied by a constant value (C). It is denoted as:
∫ f(x) dx = F(x) + C, where F'(x) = f(x)
Definite Integral
A definite integral has a specific boundary or limit for the calculation of the function. The upper and lower limits of the independent variable of a function are specified. A definite integral is given mathematically as,
∫ab f(x) · dx = F(x)
Calculus Formula
Calculus formulas can be broadly divided into the following six broad sets of formulas. The six broad formulas are related to limits, differentiation, integration, definite integrals, application of differentiation, and differential equations.
Limits Formulas: Limits formulas help in approximating the limit of a function at a given point.
limx→0 (xn - an)(x - a) = na(n - 1)
limx→0 (sin x)/x = 1
limx→0 (tan x)/x = 1
limx→0 (ex - 1)/x = 1
limx→0 (ax - 1)/x = logea
limx→∞ (1 + (1/x))x = e
limx→0 (1 + x)1/x = e
limx→0 (1 + (a/x))x = ea
Differentiation Formulas: Differentiation Formulas are applicable to basic algebraic expressions, trigonometric ratios, inverse trigonometry, and exponential terms.
d/dx (xn) = nxn - 1
d/dx (Constant) = 0
d/dx (ex) = ex
d/dx (ax) = ax · ln a
d/dx (ln x) = 1/x
d/dx (sin x) = cos x
d/dx (cos x) = -sin x
d/dx (tan x) = sec2x
d/dx (cot x) = -cosec2x
d/dx (sec x) = sec x · tan x
d/dx (cosec x) = -cosec x · cot x
Integration Formula: Integrals formulas can be derived from differentiation formulas, and are complimentary to differentiation formulas.
∫ xn dx = xn + 1/(n + 1) + C
∫ 1 dx = x + C
∫ ex dx = ex + C
∫(1/x) dx = ln |x| + C
∫ ax dx = (ax/log a) + C
∫ cos x dx = sin x + C
∫ sin x dx = -cos x + C
∫ sec2x dx = tan x + C
∫ cosec2x dx = -cot x + C
∫ sec x tan x dx = sec x + C
∫ cosec x cot x dx = -cosec x + C
Definite Integrals Formulas: Definite integrals are the basic integral formulas and are additionally having limits. There is an upper and a lower limit in definite integrals, that are helpful in finding the area within these limits.
∫ba f'(x) dx = f(b) - f(a), this is known as fundamental theorem of calculus
∫ba f(x) dx = ∫ba f(t) dt
∫ba f(x) dx = - ∫ab f(x) dx
∫ba f(x) dx = ∫ca f(x) dx + ∫bc f(x) dx
∫ba f(x) dx = ∫ba f(a + b - x) dx
∫a0 f(x) dx = ∫a0 f(a - x) dx
∫a-a f(x) dx = 2∫a0 f(x) dx, f is an even function
∫a-a f(x) dx = 0 , f is an odd function
Application of Differentiation Formulas: The application of differentiation formulas is useful for approximation, estimation of values, equations of tangents and normals, maxima and minima, and for finding the changes of numerous physical events.
dy/dx = (dy/dt)/(dx/dt)
Equation of a Tangent: y - y1 = dy/dx · (x - x1)
Equation of a Normal: y - y1 = -1/(dy/dx) · (x - x1)
Differential Equations Formula: Differential equations are equations involved with derivatives. In the general equation, we have the unknown variable 'x' and here we have the differentiation dy/dx as the variable of the equation.
Homogeneous Differential Equation: f(λx, λy) = λnf(x, y)
Linear Differential Equation: dy/dx + Py = Q. The general solution of linear differential equation is y.e- ∫P dx = ∫(Q · e∫P dx) dx + C
Applications of Calculus
Calculus is a very important branch, a mathematical model that helps in:
- Analyzing a system to find an optimal solution to predict the future of any given condition for a function.
- Concepts of calculus play a major role in real life, either it is related to solve the area of complicated shapes, evaluating survey data, the safety of vehicles, business planning, credit card payment records, or finding the changing conditions of a system that affect us, etc.
- Calculus is a language of economists, biologists, architects, medical experts, statisticians. For example, Architects and engineers use different concepts of calculus in determining the size and shape of the construction structures.
- Calculus is used in modeling concepts like birth and death rates, radioactive decay, reaction rates, heat and light, motion, electricity, etc.
☛ Related Topics
Calculus Problems
-
Example 1: Let f(y) = y2 and g(y) = ey. Use the chain rule in calculus to calculate h′(y) where h(y) = f(g(y)).
Solution:
Given, f(y) = y2 and g(y) = ey. First derivative of above functions are f'(y) = 2y and g'(y) = ey
To find: h′(y)
Now, h(y) = f(g(y))
By chain rule of differentiation,
h'(y) = f'(g(y)) g'(y)
h'(y) = f'(ey) eyBy substituting the values.
h'(y) = 2ey × ey
or h'(y) = 2e2yAnswer: ∴ h'(y) = 2e2y
-
Example 2: y is a function of x, and the function definition is given as: y = f(x) = 1/(1 + x2). Find the output values of the function for x = 0, x = −1, and x = √2.
Solution:
We have:
f(0) = 1/[1 + (0)2] = 1/1 = 1
f(−1) = 1/[1 + (−1)2] = 1/2
f(√2) = 1/[1 + (√2)2] = 1/3
Answer: ∴ f(0) = 1, f(-1) = 1/2, and f(√2) = 1/3
-
Example 3: Find the slope of the tangent of the curve y = 2x2 + 3x + 1, at the point (-1, 0)
Solution:
The given equation of the curve is y = 2x2 + 3x + 1.
The aim is to find the slope of the tangent at the given point and hence we need to differentiate the equation.
d/dx (y) = d/dx (2x2 + 3x + 1)
dy/dx = 4x + 3
The slope at at point (-1, 0) is m = 4(-1) + 3 = -1Answer: Hence the slope of the tangent at the given point is -1
-
Example 4: Differentiate x tan x.
Solution:
By product rule from in differential calculus,
d/dx (x tan x) = x (d/dx (tan x)) + tan x (d/dx (x))
Using calculus formulas,
d/dx (x tan x) = x sec2x + tan x · 1
= x sec2x + tan xAnswer: d/dx (x tan x) = x sec2x + tan x

FAQs on Calculus
What is Calculus in Maths?
Calculus is a field of mathematics that revolves around the investigation of change and motion. It utilizes differentiation and integration to examine rates of change, the slope of a curve, and the accumulation of quantities.
What are Important Calculus Formulas?
A few of the important formulas used in calculus to solve complex problems are as listed below,
- Ltx→0 (xn - an)(x - a) = na(n - 1)
- ∫ xn dx = xn + 1/(n + 1) + C
- ∫ ex dx = ex + C
- d/dx (xn) = nxn - 1
- d/dx (Constant) = 0
- d/dx (ex) = ex
For the list of all formulas, scroll up this page or click here.
What is Differential Calculus?
Differential calculus is a part of calculus that studies the instantaneous rate of change of a function. It involves concepts such as derivatives and limits to analyze the slope of curves and to determine critical points.
What do you Use Calculus for?
- Calculus is used in physics where the concept of differentiation and integration is involved in finding the displacement, velocity, acceleration, etc.
- It is used in optimizing functions.
- Calculus is widely used in finance and economics to find the maximum profit, minimum cost, etc.
- Calculus is also used in biology and medicine to analyze drug dosage, estimate population growth/decay, etc.
What is Basic Calculus?
Basic calculus refers to fundamental concepts that help with further exploration of calculus and its applications. It basically deals with limits, differentiation, and integration.
How to Find the Maxima and Minima of a Function in Calculus?
Derivatives are used to calculate the maxima and minima values of a function. Maxima and minima are the highest and lowest points of a function respectively, which could be determined by finding the derivative of the function.
What are the Four Main Concepts of Calculus?
The four main concepts covered under calculus are as given below,
- Limits
- Differential Calculus
- Integral Calculus
- Multivariable Calculus
What is Integral Calculus?
Integral calculus is a division of calculus that deals with the accumulation of quantities over a given interval. It involves the calculation of areas under curves. Some of its applications are calculating total displacement, total cost, total accumulated value, etc.
What are the Differences Between Basic Calculus and Advanced Calculus?
Here are some differences between basic and advanced calculus.
| Basic Calculus | Advanced Calculus |
|---|---|
| Deals with fundamental concepts. | Deals with specialized concepts. |
| Covers limits, derivatives, and integrals. | Covers series and convergence, partial derivatives, double and triple integrals. |
| Deals with simple functions. | Deals with more complex functions. |
visual curriculum