Inverse Proportion
When two quantities are related to each other inversely, i.e., when an increase in one quantity brings a decrease in the other and vice versa then they are said to be in inverse proportion. In inverse proportion, the product of the given two quantities is equal to a constant value. Let's learn more about it in detail in this article.
| 1. | What is Inverse Proportion? |
| 2. | Inverse Proportion Formula |
| 3. | Inverse Proportion Graph |
| 4. | Direct and Inverse Proportion |
| 5. | FAQs on Inverse Proportion |
What is Inverse Proportion?
The definition of inverse proportion states that "Two quantities are said to be in inverse proportion if an increase in one leads to a decrease in the other quantity and a decrease in one leads to an increase in the other quantity". In other words, if the product of both the quantities, irrespective of a change in their values, is equal to a constant value, then they are said to be in inverse proportion. For example, let us take the number of workers and the number of days required by them to complete a given amount of work as x and y respectively.
| Numbers of Workers (x) | Number of Days Required (y) |
|---|---|
| 16 | 3 |
| 12 | 4 |
| 8 | 6 |
| 4 | 12 |
Are the number of workers and the number of days in inverse proportional relation? Let's find out.
Observe the values written in the table carefully. You will find out that for each row, the product of x and y are the same. That means if there are 16 workers, they will complete the work in 3 days. So, here x × y = 16 × 3 = 48. Now, we decrease the number of workers, it is obvious that the less number of workers will do the same work in more time. But we see the product of x and y here, it is 12 × 4 = 48. Again, for 8 workers in 6 days, the product is 48. And same for 4 workers in 12 days. So, the product of two quantities in inverse proportion is always equal.
Inverse Proportion Formula
Inverse proportion formula help in establishing a relationship between two inversely proportional quantities. Let x and y be two quantities and assume that x is decreasing when y is increasing and vice versa. Example: The speed is inversely proportional to the time. As the speed increases, the time taken by us to cover the same distance decreases. Taking speed as y and time as x, we can say that y is said to be inversely proportional to x and is written mathematically as inverse proportion formula.
The inverse proportional formula is written as
y = k/x
where
- k is the constant of proportionality.
- y increases as x decreases.
- y decreases as x increases.
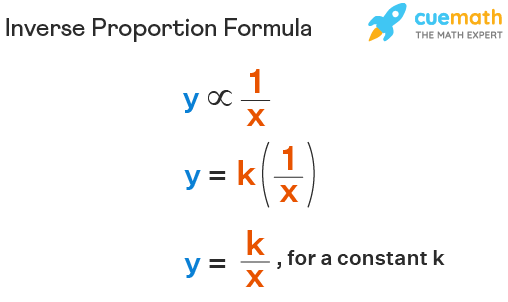
Here the symbol ∝ denotes the proportional relationship between two quantities.
Inverse Proportion Graph
The graph of inverse proportion is usually a curve that bends towards the origin forming the shape of a hyperbola. If there are any two random points each on the x-axis and y-axis on the inverse proportion graph (x)1, (x)2, (y)1, and (y)2, such that (x)1 < (x)2 and (y)1 < (y)2, the graph will be shown like this:
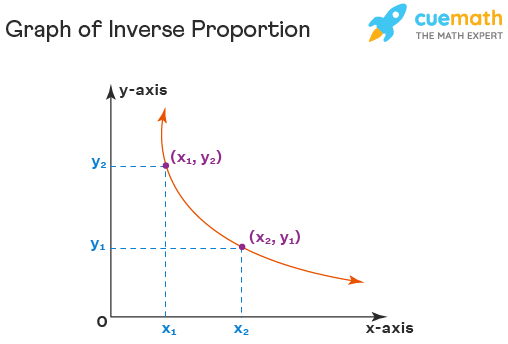
It means if we are increasing the value of x from \(x_{1}\) to \(x_{2}\), the value of y decreases from \(y_{2}\) to \(y_{1}\).
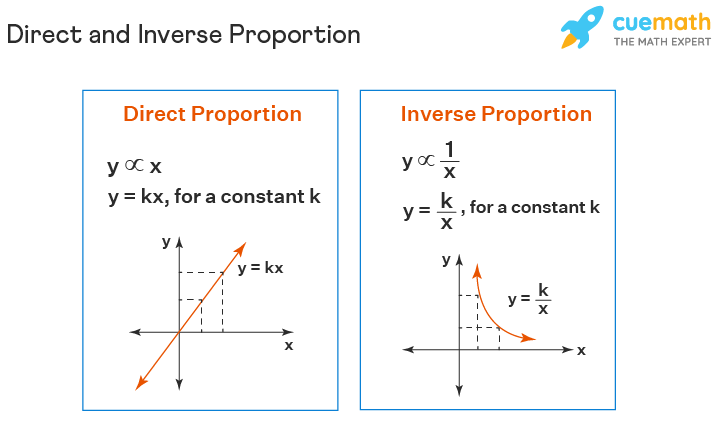
Direct and Inverse Proportion
There are two main types of proportionality - direct proportion and inverse proportion. Two variables x and y are said to be in direct proportion when y ∝ x (or x ∝ y). This implies, y = kx, for a constant k. While two variables x and y are said to be in inverse proportion if y ∝ 1/x (or x ∝ 1/y). This implies y = k/x, for a constant k. In a direct variation relationship, the ratio of two variables is equal for any values, while in inverse proportion the product of two variables is equal for any values. Look at the image given below to understand the distinction between direct and inverse proportion pictorially.
Related Topics
Check these interesting articles related to the concept of inverse proportion.
Inverse Proportion Examples
-
Example 1: Suppose x and y are in an inverse proportion such that when x = 120, y = 5. Find the value of y when x = 150 using the inverse proportion formula.
Solution:
To find: Value of y.
Given: x = 120 when y = 5.
x ∝ 1/y
x = k / y, where k is a constant,
or k = xy
Putting, x = 120 and y = 5, we get;
k = 120 × 5 = 600
Now, when x = 150, then;
150 y = 600
y = 600/150 = 4
That means when x is increased to 150 then y decreases to 4.Answer: The value of y is 4 when x = 150.
-
Example 2: The time taken by a vehicle is 3 hours at a speed of 60 miles/hour. What would be the speed taken to cover the same distance at 4 hours?
Solution:
Consider speed as m and time parameter as n.
If the time taken increases, then the speed decreases. This is an inverse proportional relation, hence m ∝ 1/n.
Using the inverse proportion formula,
m = k/ n
m × n = k
At speed of 60 miles/hour, time = 3 hours, from this we get,
k = 60 × 3 = 180
Now, we need to find speed when time, n = 4.
m × n = k
m × 4 = 180
∴ m = 180/4 = 45Therefore, the speed at 4 hours is 45 miles/hour.
-
Example 3: In a construction company, a supervisor claims that 7 men can complete a task in 42 days. In how many days will 14 men finish the same task?
Solution:
Consider the number of men be M and the number of days be D.
Given: \(M_1\)= 7 , \(D_1\) = 42, and \(M_2\) = 14.This is an inverse proportional relation, as if the number of workers increases, the number of days decreases.
M ∝ 1/D
Considering the first situation, \(M_1\) = k/ \(D_1\)
7 = k/42
k = 7 × 42 = 294
Considering the second situation, \(M_2\) = k/ \(D_2\)
14 = 294/ \(D_2\)
\(D_2\) = 294/14 = 21
Answer: It will take 21 days for 14 men to do the same task.

FAQs on Inverse Proportion
What is an Indirect Proportion?
Indirect or inverse proportion is a relation between two quantities where an increase in one leads to a decrease in the other, and vice-versa. It is just the opposite of direct proportion.
What is the Symbol ∝ Denotes in Inverse Proportion Formula?
In the inverse proportion formula, the proportionate symbol ∝ denotes the relationship between two quantities. It is expressed as x ∝ 1/y. This implies x = k/y, where k is the constant of proportionality.
How do you Find K in Inverse Proportion?
K in inverse proportion represents the constant of proportionality which is the same irrespective of the values of the given variables. To find k in inverse proportion, find the product of x and y. The formula is y = k/x, which gives us k=xy.
How do you Represent the Inverse Proportional Formula?
The inverse proportional formula depicts the relationship between two quantities which can be understood by the formula given below:
- Identify the two quantities which vary in the given problem.
- Identify that there is an inverse variation. x ∝ 1/y
- Apply the Inverse proportion formula x = k/y.
What is the Difference Between Direct and Inverse Proportion?
The difference between direct and inverse proportion is that the direct proportion shows a direct relationship between the two quantities where an increase in one also leads to an increase in the other quantity and vice-versa. On the other hand, inverse proportion represents an indirect relation between two quantities or variables where an increase in one leads to a decrease in the other variable, and vice-versa.
What is the Formula of Inverse Proportion?
The formula of inverse proportion is y = k/x, where x and y are two quantities in inverse proportion and k is the constant of proportionality.
How to Show Relationship Between Two Quantities Using Inverse Proportion Formula?
The inverse proportional relationship between two quantities can be shown if the product of two quantities (x × y) is constant, then they depict an inversely proportional relationship. It is expressed as x ∝ 1/y or x = k/y, where k is the constant of proportionality.
visual curriculum