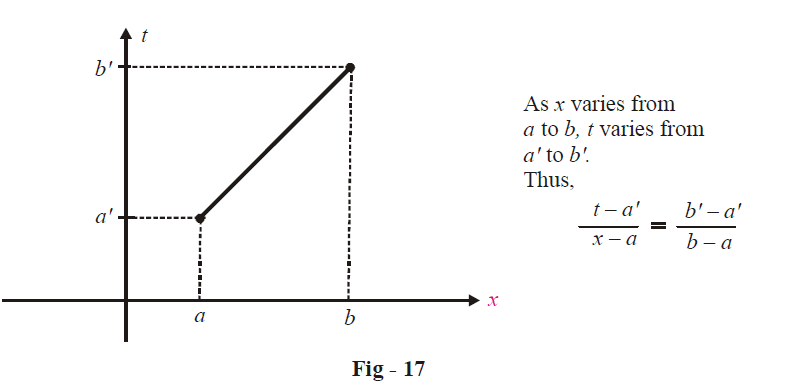(12) Sometimes, it is convenient to change the limits of integration into some other limits. For example, suppose we have to add two definite integrals \({I_1}{\rm{ and }}{I_2}\) ; the limits of integration for these integrals are different. If we could somehow change the limits of \({I_2}\) into those of \({I_1}\) or vice-versa, or in fact change the limits of both \({I_1}{\rm{ and }}{I_2}\) into a third (common) set of limits, the addition could be accomplished easily.
Suppose that \(I = \int\limits_a^b {f(x)\;dx} \) . We need to change the limits (a to b) to (a' to b'). As x varies from a to b, we need a new variable t (in terms of x) which varies from a' to b'.
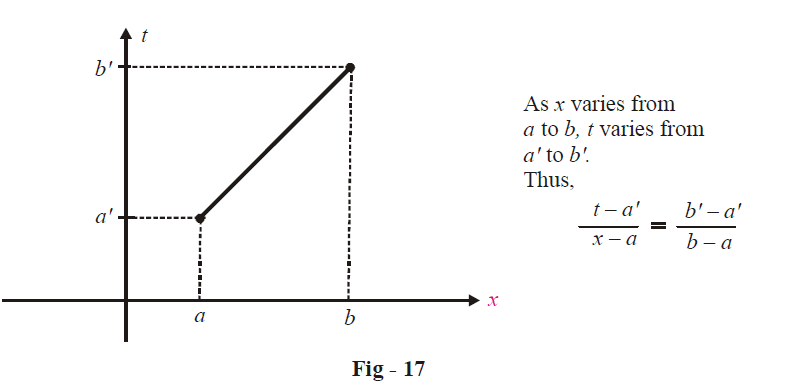
As described in the figure above, the new variable t is given by,
\[t = a' + \left( {\frac{{b' - a'}}{{b - a}}} \right)(x - a)\]
Thus,
\[\begin{align}&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,dt = \frac{{b' - a'}}{{b - a}}dx\\ &\;\Rightarrow \quad I = \int\limits_a^b {f(x)\,dx} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, &\qquad\quad= \int\limits_{a'}^{b'} {f\left( {a + \left( {\frac{{b - a}}{{b' - a'}}} \right)(t - a')} \right)\left( {\frac{{b - a}}{{b' - a'}}} \right)\,dt} \end{align}\]
The modified integral has the limits \((a'\,\,{\rm{to }}\;b')\) . A particular case of this property is modifying the arbitrary integration limits (a to b) to (0 to 1) i.e., \(a' = 0\,\,{\rm{and }}\;b' = 1\) . For this case,
\[\begin{array}{l}I = \int\limits_a^b {f(x)\;dx} \\\,\,\,\, = (b - a)\int\limits_0^1 {f(a + (b - a)t)\,dt} \end{array}\]