Examples On Differentiability Set-1

Example – 19

 If \(f\left( x \right) = \left\{ {\begin{align}&{3 - {x^2}} {\qquad, - 1 \le x < 2}\\&{2x - 4} {\qquad,2 \le x \le 4}\end{align}} \right\}\)  , discuss its continuity and differentiability.

Solution: In questions involving evaluation of continuity and differentiability, we can of course proceed analytically by writing down the expressions for LHD and RHD (at those points where we feel the function might not be continuous or differentiable); but we will always try to follow a graphical approach also, wherever possible, since it gives much useful information about the behaviour of the function.

Note that in piecewise defined functions such as the one above we have to use different definitions of  f (x) in different intervals. So for example, to evaluate f (a – h) we will have to use the function definition for x < a, whereas for f (a + h) we have to use the definition for x > a.

In this question, there is only one point, namely x = 2, where this function could be possibly discontinuous and /or non-differentiable. The two functions    \(3{\rm{ }}-{x^2}\) and 2x – 4 are otherwise continuous and differentiable in their separate intervals. Hence, we need to analyse the continuity and differentiability only at x = 2{such points are sometimes referred to as critical points}

Analytical approach:

\[\begin{align}{\rm{LHL}}\left( {{\rm{at }}x = 2} \right)&= \mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right)\\&= \mathop {\lim }\limits_{x \to 2} \left( {3 - {x^2}} \right)\\
&= - 1\\
{\rm{RHL}}\left( {{\rm{at }}x = 2} \right) &= \mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right)\\&= \mathop {\lim }\limits_{x \to 2} 2x - 4\\&= 0\end{align}\]

\[\begin{align}f\left( 2 \right)&= 2\left( 2 \right) - 4 \quad \left\{ \begin{gathered}{\text{Note that we used the lower function to }}\\ {\rm{evaluate\,\, }}f{\rm{(2) because \,\,of \,\,the\,\, placement \,\,of }}\\ {\rm{equality\,\, sign}}\,{\rm{with\,\, 2 \,\,in }}\,\,{\rm{2}}x - {\rm{4,}}\,\,\,\,{\rm{2}} \le x \le {\rm{4}}  \end{gathered}\right\}\\&=0\end{align}\]

This function is discontinuous at x = 2 and therefore also non-differentiable.

\[\begin{align}& LHD\left( {{\rm{at}}\;x = 2} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {2 - h} \right) - f\left( 2 \right)}}{h}\\&\qquad\qquad\qquad{\rm{       }}\,\,\,\,\,\, = \infty \end{align}\]

This is because there is a finite positive change in the function’s value in going from 2^–  to 2.

\[\begin{align}&RHD\left( {{\rm{at}}\;x = 2} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {2 + h} \right) - f\left( 2 \right)}}{h}\\&\qquad\qquad\qquad\quad= 2\end{align}\]

Example – 20

A function f (x) is defined as:

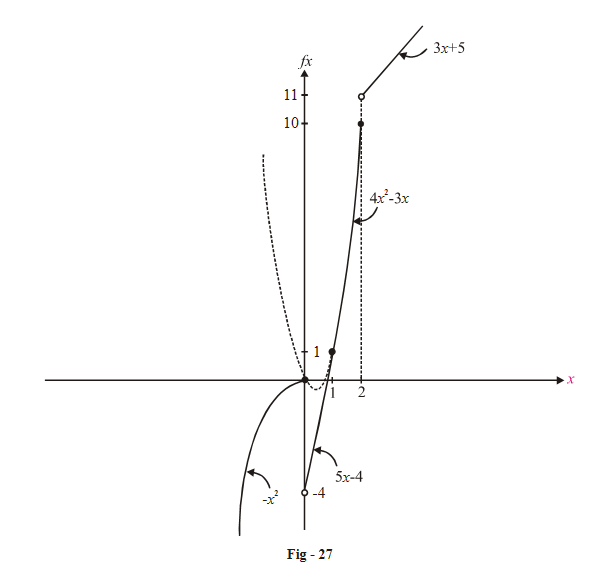
\(f\left( x \right) = \left\{ {\begin{align}&{ - {x^2}\,,}&{x \le 0}\\&{5x - 4\,,}&{0 < x \le 1}\\&{4{x^2} - 3x\,,}&{1 < x \le 2}\\&{3x + 5\,,}&{x > 2}\end{align}} \right\}\). Discuss the continuity and differentiability of f(x).

Solution:    The critical points for this function are x = 0, 1, 2.

Lets analyse f (x) for each of these critical points separately.

 (i) \(\boxed{x = 0 \left\{ {f\left( 0 \right) = 0} \right\}}\)

    \[\begin{align}&{\rm{LHL}} = \mathop {\lim }\limits_{x \to {0^ - }} \left( { - {x^2}} \right) = 0\\& {\rm{LHD}} = \mathop {\lim }\limits_{h \to 0} \frac{{ - {{\left( { - h} \right)}^2} - 0}}{{ - h}} = 0\\ &{\rm{RHL}} = \mathop {\lim }\limits_{h \to {0^ + }} \left( {5x - 4} \right) = - 4\\&{\rm{RHD}} = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( h \right) - f\left( 0 \right)}}{h}\\&\quad\quad{\rm{ }} = \mathop {\lim }\limits_{h \to 0} \frac{{5h - 4}}{h} = - \infty \end{align}\]

Therefore, this function is non-continuous (and non-differentiable) at x = 0.

(ii) \(\boxed{x = 1\,\,\,\,\left\{ {f\left( 1 \right) = 1} \right\}}\)

\[\begin{align}{\rm{LHL}}& = \mathop {\lim }\limits_{x \to {1^ - }} \left( {5x - 4} \right) = 1\\{\rm{LHD}} & = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {1 - h} \right) - f\left( 1 \right)}}{h}\\\quad\quad{\rm{ }} &= \mathop {\lim }\limits_{h \to 0} \frac{{5\left( {1 - h} \right) - 4 - 1}}{{ - h}}\\&\qquad{\rm{ }} = {\rm{ }}5\\{\rm{RHL}} &= \mathop {\lim }\limits_{h \to {1^ + }} \left( {4{x^2} - 3x} \right) = 1\\{\rm{RHD}}& = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {1 + h} \right) - f\left( 1 \right)}}{h}\\\quad\quad{\rm{ }}& = \mathop {\lim }\limits_{h \to 0} \frac{{4{{\left( {1 + h} \right)}^2} - 3\left( {1 + h} \right) - 1}}{h}\\\quad\quad{\rm{ }}& = {\rm{ }}5 \end{align}\]

Since LHL = RHL and LHD = RHD, f (x) is continuous and differentiable at x = 1

(iii)              \(\boxed{x = 2\left\{ {f\left( 2 \right) = 10} \right\}}\)

\[\begin{align}{\rm{LHL}}&= \mathop {\lim }\limits_{x \to {2^ - }} \left( {4{x^2} - 3x} \right) = 10\\{\rm{LHD}} &= \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {2 - h} \right) - f\left( 2 \right)}}{h}\\\qquad{\rm{ }} &= \mathop {\lim }\limits_{h \to 0} \frac{{\left\{ {4{{\left( {2 - h} \right)}^2} - 3\left( {2 - h} \right)} \right\} - 10}}{{ - h}}\\\qquad{\rm{ }} &= {\rm{ }}13\\ {\rm{RHL}} &= \mathop {\lim }\limits_{x \to {2^ + }} \left( {3x + 5} \right) = 11\\{\rm{RHD}} &= \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {2 + h} \right) - f\left( 2 \right)}}{h} \,\\\qquad{\rm{ }} &= \mathop {\lim }\limits_{h \to 0} \frac{{\left\{ {3\left( {2 + h} \right) + 5} \right\} - 10}}{h}\\{\rm{ }} \qquad &= \infty \end{align}\]

We see that f(x) is non-continuous (and non-differentiable) at x = 0 and x = 2.

The graph is plotted below:

The elaborate analysis done for this question will not be done for subsequent questions where we will try focus more on the graphical approach.