Numbers
Numbers are an integral part of our everyday lives, right from the number of hours we sleep at night to the number of rounds we run around the racing track and much more. In math, numbers can be even and odd numbers, prime and composite numbers, decimals, fractions, rational and irrational numbers, natural numbers, integers, real numbers, rational numbers, irrational numbers, and whole numbers. In this chapter, we will get an introduction to the different types of numbers and to all the concepts related to them.
What are Numbers?
A number is a basic component of mathematics. Numbers are used for counting, measuring, keeping things in order, indexing, etc. We have different types of numbers based on their properties such as natural numbers, whole numbers, rational and irrational numbers, integers, real numbers, complex numbers, even and odd numbers, etc. We can apply the basic fundamental arithmetic operations of numbers and determine the resulting number. Initially, tally marks were used before the use of numbers. Let us now introduce the concept of numbers and understand their different types and their properties.
Definition of Numbers
An arithmetic value that is expressed using a word, a symbol or a figure that represents a quantity is called a number. Numbers are used in counting and calculations.
Introduction to Numbers
Numbers form the basis of mathematics. We should befriend numbers in order to understand math. Numbers are of various kinds. We have a long list that includes ordinal numbers, consecutive numbers, odd numbers, even numbers, natural numbers, whole numbers, integers, real numbers, rational numbers, irrational numbers, and complex numbers.
Along with numbers, we come across the interesting world of factors and multiples. This world includes prime numbers, composite numbers, co-prime numbers, perfect numbers (yes, numbers could be perfect!) HCF, LCM, and prime factorization.
Let us get started on our journey of numbers. You can go ahead and explore all important topics in Numbers by selecting the topics from the list given below:
Pre-number Math
Building pre-number math skills is a prerequisite to understanding numbers. Pre-number skills like matching, sorting, classifying, ordering, and comparing sets the stage to build a strong number sense. Pre-number Math skills are built-in preschool years. Kids learn how to stand before they start taking small steps. In the same way, the pre-number concept is very important for them to start understanding Mathematics. In this section, we will cover the different pre-number concepts like Matching and Sorting, Comparing and Ordering, Classification, and Shapes and patterns.
Example: Observe the figure given below which shows 2 columns. The left column displays the numbers 1 to 4. The right column displays rows of items. The numbers are matched to the quantities they represent. This is an essential skill for children aged 3 to 4 years.

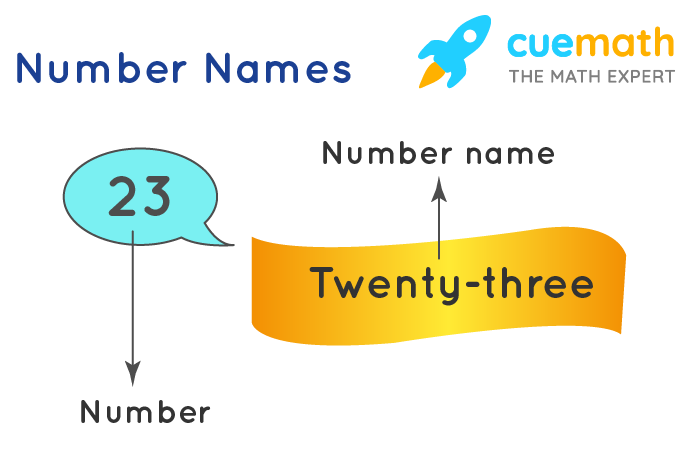
Number Names
Number names are used to represent numbers in an alphabetical format. A specific word is used to refer to each number. To write a number in words in English, we should know the place value of each digit in the number.
Example: Observe the figure given below which shows that 23 is written as 'twenty-three' in the number names form.
PEMDAS
The rules of PEMDAS outline the order of the operations and give structure to nested operations. In mathematics, PEMDAS is an acronym that stands for P- Parentheses, E- Exponents, M- Multiplication, D- Division, A- Addition, and S- Subtraction.

Let us learn in detail the different concepts of PEMDAS such as Addition, Subtraction, Multiplication, and Division.
Number Systems
The decimal number system is the most commonly used number system. The digits 0 to 9 are used to represent numbers. A digit in any given number has a place value. The decimal number system is the standard system for denoting integers and non-integers. We use the decimal number system for the representation of Numbers up to 2-Digits, Numbers up to 3-Digits, Numbers up to 4-Digits, Numbers up to 5-Digits, Numbers up to 6-Digits, Numbers up to 7-Digits, Numbers up to 8-Digits, Numbers up to 9-Digits and Numbers up to 10-Digits.
Types of Numbers
The different types of numbers depend on the properties that they have. For example, natural numbers are counting numbers that start from 1, whereas, whole numbers start from 0, prime numbers are only divisible by 1 and the number itself, and so on. Let us learn more about the different types of numbers in the following sections.
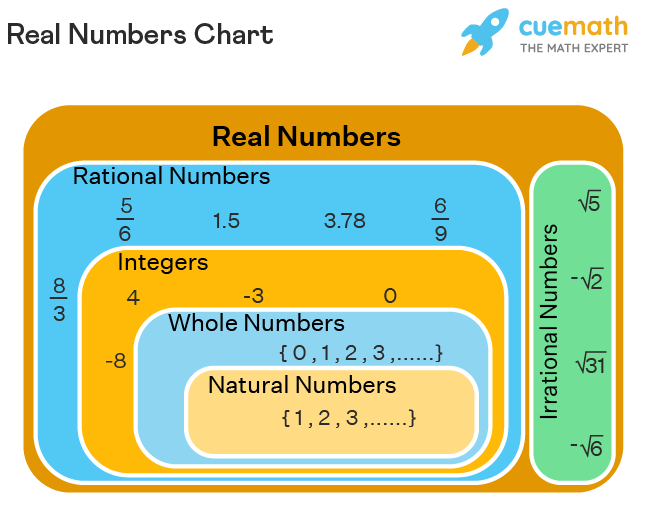
Numbers Chart
There are different types of numbers that are used, but the most commonly used numbers can be classified as per their unique properties. Observe the numbers chart which shows the types of numbers that are included under real numbers and all numbers apart from real numbers are termed as complex numbers.
Cardinal Numbers and Ordinal Numbers
A cardinal number is a number that denotes the count of any object. Any natural number such as 1, 2, 3, etc., is referred to as a cardinal number, whereas, an ordinal number is a number that denotes the position or place of an object. For example, 1st, 2nd, 3rd, 4th, 5th, etc. It indicates the order of things or objects, such as first, second, third, fourth, and so on.
Example: Observe the table given below which shows the difference between Cardinal numbers and Ordinal numbers. Ordinal numbers help define the position of the children. Such as, Jim is the fourth child from the left.

Consecutive Numbers
Consecutive numbers are numbers that follow each other in order from the smallest number to the largest number. They usually have a difference of 1 between every two numbers.
Example: Observe the figure given below which shows a list of consecutive numbers.

Integers
Integers are numbers that consist of whole numbers and negative numbers. All integers are represented by the alphabet Z and do not have a decimal or a fractional part. A number line is full of integers. On the left side, you can find negative integers while on the right side you have the positive ones. Don’t forget the zero in between!
Z = { ...., -4, -3, -2, -1, 0 , 1, 2, 3, 4,....}
Natural Numbers and Whole Numbers
A natural number is a non-negative integer and is always greater than zero. It is represented by the symbol N. It should be noted that whole numbers do not contain any decimal or fractional part. They are represented by the symbol W.

Even Numbers and Odd Numbers
Even numbers are those numbers that can be divided into two equal groups or pairs and are exactly divisible by 2. For example, 2, 4, 6, 8, 10, and so on. In other words, these are whole numbers that are exactly divisible by 2.
Example: Observe the following figure which shows that even numbers are completely divisible by 2.

Odd numbers are whole numbers that cannot be completely divided by 2. These numbers cannot be arranged in pairs. Interestingly, all the whole numbers except the multiples of 2 are odd numbers.
Example: Observe the following figure which shows that odd numbers are not completely divisible by 2 and when they are divided by 2 we get 1 as the remainder.

Prime Numbers and Composite Numbers
A prime number is a number that has exactly two factors, 1 and the number itself. For example, 2, 5, 7, 11, and so on are prime numbers. It can be said that any whole number greater than 1 that has exactly two factors, 1 and itself is defined to be a prime number.
Well, now we know that a prime number has just two factors,1 and the number itself.
A composite number is a number that has more than two factors, which means it can be divided by the number 1 and itself, and at least one more integer. It can also be said that any number greater than 1 that is not a prime number, is defined to be a composite number. Composite numbers always have more than 2 factors. For example, 6, 8, 9, 12, and so on are composite numbers because these numbers have more than 2 factors.
- Factors of 6 = 1, 2, 3, 6 (factors other than 1 and 6)
- Factors of 8 = 1, 2, 4, 8 (factors other than 1 and 8)
- Factors of 9 = 1, 3, 9 (factors other than 1 and 9)
- Factors of 12 = 1, 2, 3, 4, 6, 12 (factors other than 1 and 12)
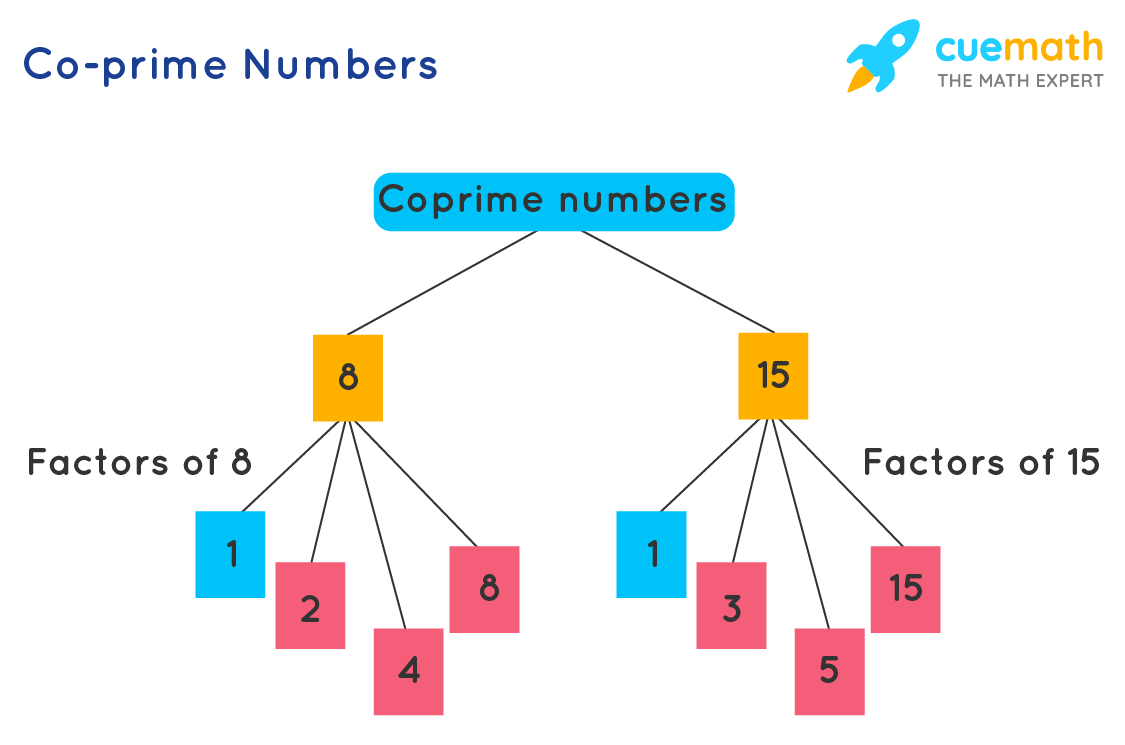
Co-prime Numbers
If a pair of numbers has no common factor apart from 1, then they are called co-prime numbers. In other words, a set of numbers or integers which have only 1 as their common factor, which means their highest common factor (HCF) will be 1, are co-primes. These are also known as mutually prime numbers or relatively prime numbers. Also, there should be two numbers in order to form co-primes.
Example: The following figure shows two co-prime numbers 8 and 15 that have only 1 as their common factor.
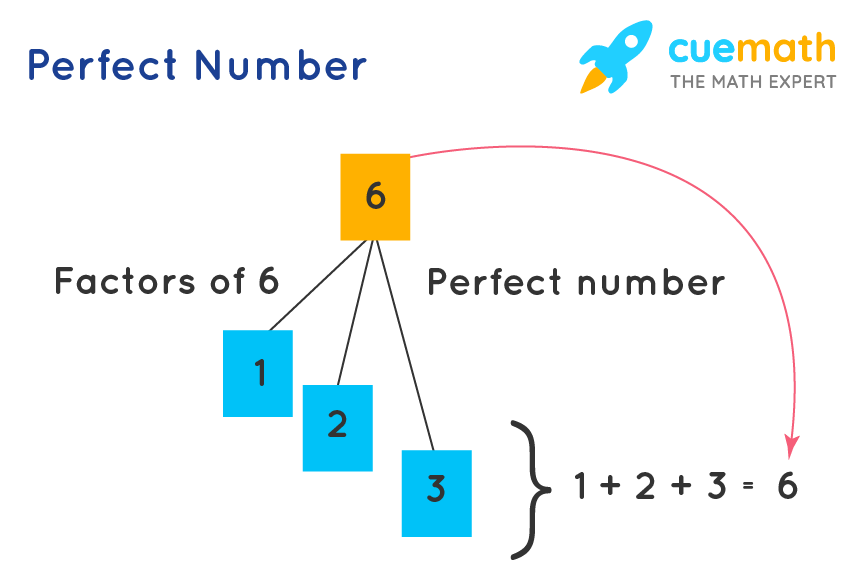
Perfect Numbers
Perfect numbers are the positive integers that are equal to the sum of its factors except for the number itself. In other words, perfect numbers are the positive integers that are the sum of their proper divisors. The smallest perfect number is 6, which is the sum of its proper divisors: 1, 2 and 3
Example: The following figure shows that 6 is a perfect number because the sum of its factors (1,2,3) leads to 6.
Fractions and Decimals
Fractions are a part of a whole. They are represented by numbers that have two parts to them and they are separated by a fraction bar. There is a number at the top, which is called the numerator, and the number at the bottom is called the denominator.
Example: The following figure shows a fraction in which 1 is the numerator and 4 is the denominator.

Now that we already know about fractions and how it is represented, some more fraction-related topics can be explored on pages like Equivalent Fractions, Improper Fractions and Mixed Fractions, Addition and Subtraction of Fractions, Multiplication of Fractions and Division of Fractions.
What about Decimals? A decimal number has a whole number part and a fractional part. These parts are separated by a decimal point.
Example: Observe the figure given below which shows a decimal number that has a whole number part and a fractional part.
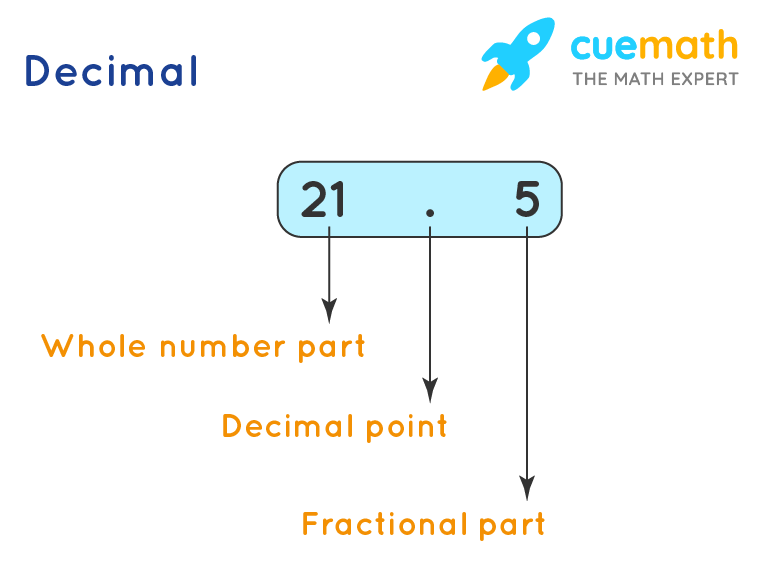
Decimals are really interesting. They have a whole number part and they can also be represented as fractions. Some more decimal-related concepts can be explored on pages like, Addition and Subtraction of Decimals, Multiplication of Decimals, and Division of Decimals.
Rational Numbers and Irrational Numbers
A rational number, denoted by Q, is represented in the form p/q, where q is not equal to zero. Integers, Fractions, Decimals, Whole numbers, and Natural numbers are all Rational numbers. For example, 1/2, - 4/5 are rational numbers.
In order to get a better understanding of Rational numbers, other topics related to rational numbers can be studied on pages like Decimal Representation of Rational Numbers, and Operations on Rational Numbers.
Now, Irrational Numbers are the numbers that cannot be represented using integers in the p/q form. The set of irrational numbers is denoted by Q'. For example, √5, √2, and so on are irrational numbers.
Irrational numbers cannot be represented as a simple fraction. Their decimal expansion neither terminates nor becomes periodic. Some more topics related to irrational numbers can be studied on pages like Square Root of Two is Irrational, Decimal Representation of Irrational Numbers, The exactness of Decimal Representation, Rationalize the Denominator, Surds, and Conjugates and Rationalization.
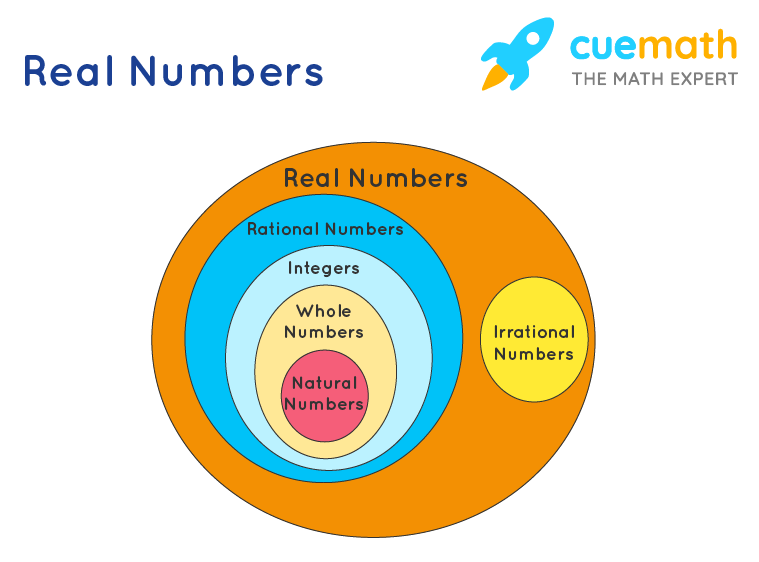
Real Numbers
Any number that can be found in the real world is a real number. Any number that we can think of, except complex numbers, is a real number. The set of real numbers is the union of the set of Rationals (Q) and Irrationals (Q'). It is denoted by R. The set of real numbers, R = Q ∪ Q'. The following figure shows the relationship between real numbers, rational numbers, irrational numbers, integers, whole numbers and natural numbers.
Complex Numbers
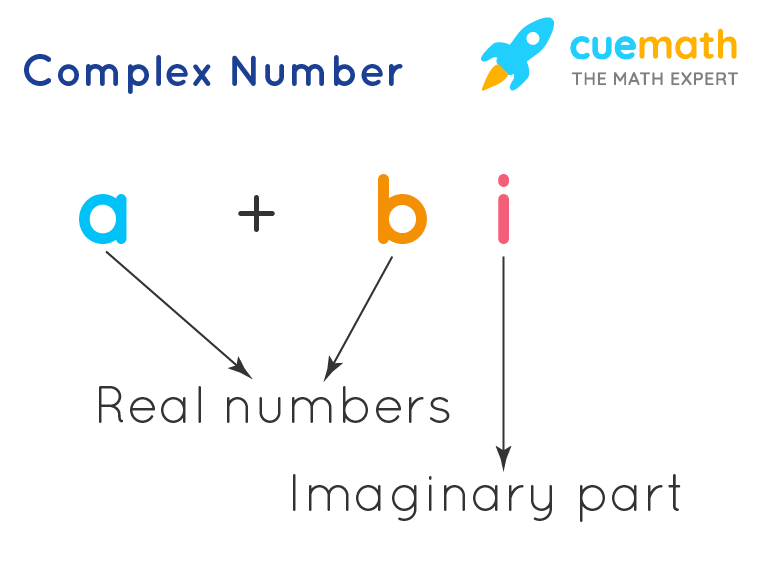
A complex number is a number that can be expressed in the form (a + bi) where a and b are real numbers, and i is a solution of the equation x2 = −1. Since no real number satisfies this equation, i is called an imaginary number. Complex numbers have a real part and an imaginary part. Wait, do you think Complex numbers are really complex? Well, let us study them in detail to find out. In this section, we cover different topics like Complex Numbers – Points in the Plane, A Complex Number is a Point in the Plane, What is i? Magnitude and Argument, Powers of iota, Addition, and Subtraction of Complex Numbers, Multiplication of Complex Numbers, Conjugate of a Complex Number, Division of Complex Numbers, Addition, Subtraction, and Interpretation of |z1-z2|.
Example: Observe the figure given below which shows that a complex number consists of real numbers and an imaginary part.
Factors and Multiples
Factors and multiples are the two key concepts that are studied together. Factors are the numbers that divide the given number completely without leaving any remainder, whereas the multiples are the numbers that are multiplied by the other number to get specific numbers.
Factors of a given number are numbers that can perfectly divide that given number.
Examples:
- Factors of 6: 1, 2, 3, 6
- Factors of 8: 1, 2, 4, 8
- Factors of 14: 1, 2, 7, 14
- Factors of 36: 1, 2, 3, 4, 6, 9, 18, 36
A multiple of a number is a number obtained by multiplying the given number by another whole number.
Examples:
- Multiples of 3: 3, 6, 9, 12, 15, ......
- Multiples of 5: 5, 10, 15, 20, 25, .....
- Multiples of 10: 10, 20, 30, 40, 50,...
- Multiples of 12: 12, 24, 36, 48, 60, ....
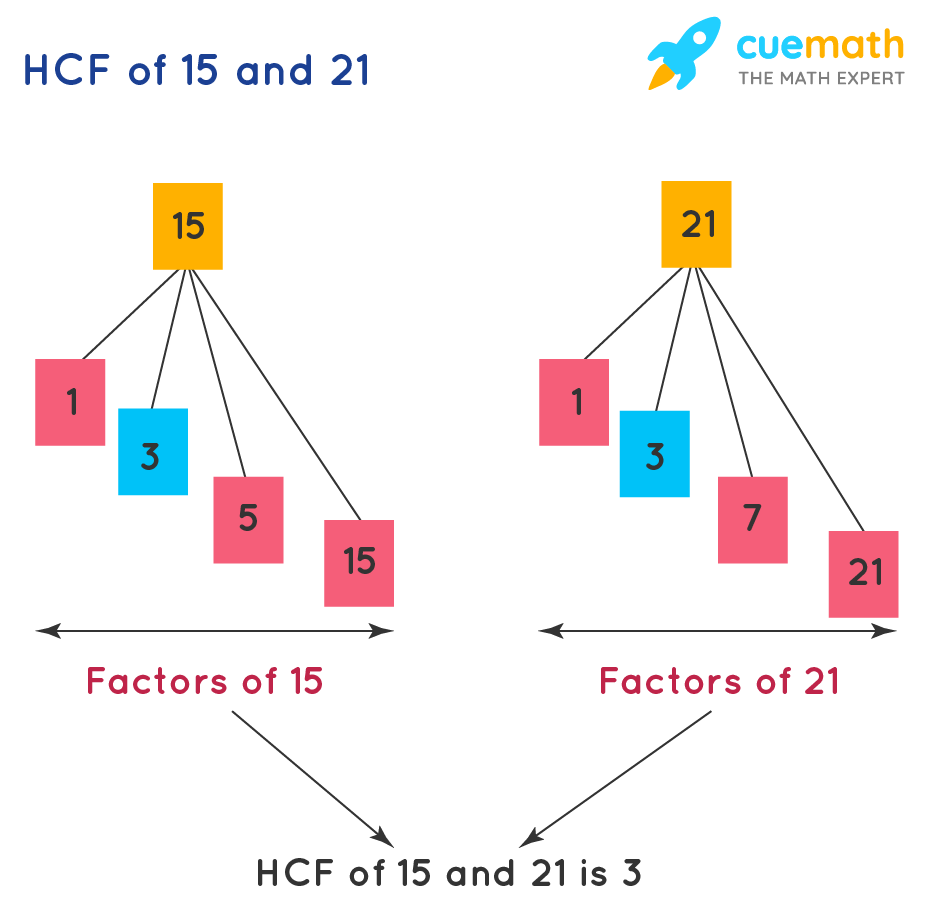
Highest Common Factor (HCF)
The Highest Common Factor (HCF) of the two numbers is the largest whole number which is a factor of both. It is also called the Greatest Common Factor(GCF).
Example: Observe the following figure which shows the HCF of 15 and 21 which is 3.
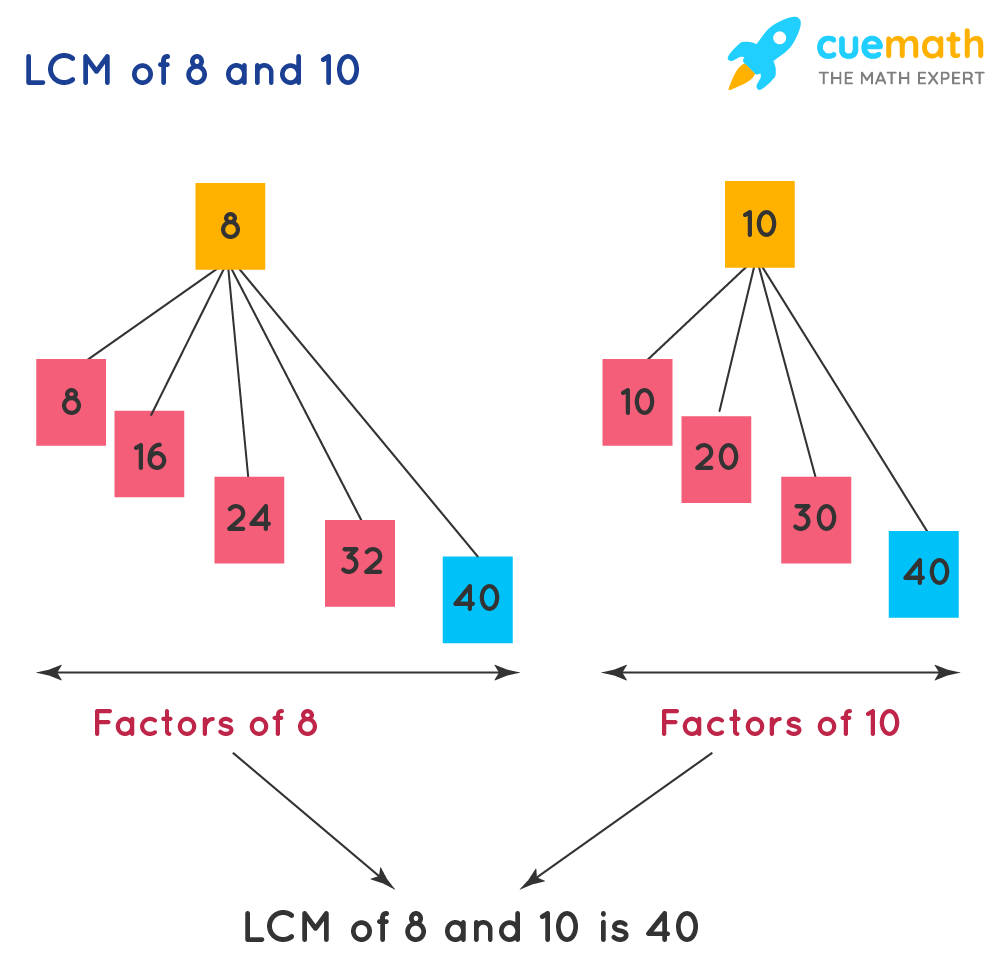
Least Common Multiple (LCM)
When we consider two numbers, each will have its own set of multiples. Some multiples will be common to both numbers. The smallest of these common multiples is called the Least Common Multiple (LCM) of the two numbers.
Example: Observe the following figure which shows the LCM of 8 and 10 which is 40.
Prime Factorization
Prime factorization allows us to write any number as a product of prime factors. It is a way of expressing a number as a product of its prime factors. To do prime factorization, we need to break a number down to its prime factors.
Example: Observe the figure given below which shows the prime factorization of 12.

Properties of Numbers
The basic properties of numbers that are used in mathematics are:
- Commutative Property: This property of numbers is applicable to addition and multiplication. It is expressed as, a + b = b + a and a × b = b × a.
- Associative Property: This property of numbers is applicable to addition and multiplication. It is expressed as, a + (b + c) = (a + b) + c and a × (b × c) = (a × b) × c.
- Distributive Property: The product of the sum of two numbers and a third number is equal to the sum of the product of each addend and the third number. It is expressed as a × (b + c) = a × b + a × c.
- Identity Property: We have an additive identity equal to 0 and a multiplicative identity equal to 1. It is written as, a + 0 = a and a × 1 = a.
- Reflexive Property: This property implies that every number is equal to itself. It is written as, for all a, a = a.
- Symmetric Property: If a number x is equal to y, then y is equal to x. It can be written as, x = y ⇒ y = x.
- Transitive Property: If x is equal to y and y is equal to z, then we can say that x = z. It is expressed as, x = y and y = z ⇒ x = z.
- Inverse Property: When an arithmetic operation is applied between a number and its inverse, we can get the identity. It is expressed as, a + (-a) = 0 and a × (1/a) = 1.
Important Notes
- The numbers which start from 1 and go up to infinity are called natural numbers.
- The numbers which start from zero are called whole numbers.
- Integers consist of positive and negative numbers along with zero.
- Rational numbers are of the form p/q and consist of integers, fractions, and ratios.
- Irrational Numbers are not expressed in the form of fractions or ratios.
- Real numbers consist of natural numbers, whole numbers, rational numbers, and irrational numbers.
☛ Related Articles
Examples on Numbers
-
Example 1: Help Ron in completing the number counting chain using pre-number math skills.
1, _, _, _, 5, _, _, _, _, 10.
Solution:
To complete the number counting chain Ron needs to observe the pattern of numbers. It starts at 1 and ends at 10. The complete number chain is as follows
1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
-
Example 2: Classify the following numbers as even numbers and odd numbers: 1, 3, 4, 7, 12, 21, 29, 32
Solution:
Even numbers are the numbers that are exactly divisible by 2. Therefore, 4, 12, and 32 are even numbers, whereas, odd numbers are the numbers that are not divisible by 2. Therefore, 1, 3, 7, 21, and 29 are odd numbers.
-
Example 3: William has a collection of number cards with the following numbers written on them. −1, √22, 11, 44, and −11. Help William pick out the natural numbers from this.
Solution:
Natural numbers are also called counting numbers that start from 1 and do not include fractions. Therefore, William can choose 11 and 44 as natural numbers.

FAQs on Numbers
What are Numbers in Math?
Numbers form the basis of mathematics. Numbers are used for counting, measuring, keeping things in order, indexing, etc. We have different types of numbers based on their properties
What is the Smallest Whole Number?
0 is the smallest whole number. Whole numbers start from 0 and go on till infinity. For example, 0, 3, 56, 879 are whole numbers.
What are the First 10 Numbers?
The first ten natural numbers can be listed as 1,2,3,4,5,6,7,8,9 and 10.
What is Not a Real Number?
All basic numbers, including irrational numbers, fall under the subset of real numbers. There is NO number that is not a real number unless it is an imaginary number. Non-real numbers cannot be expressed on a number line.
How are Numbers Formed?
A number is an arranged group of digits. Numbers can be formed with or without the repetition of digits. For example, the largest number which can be formed using 8 and 9 is 98.
Why are Numbers Important in our Life?
Numbers are a part of our everyday life. These are used in an unlimited range of ways, from mathematical calculations, mobile numbers, and phone calls, identification of bank accounts, exchange of money to cooking, etc.
What are the Basic Numbers?
The first ten numbers are known as the basic numbers in mathematics. The list of these basic numbers starts from 0 and ends at 9. The basic numbers are 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.
How Many Numbers From 1 to 100 are There?
To know the count of the total numbers from 1 to 100 we need to count one by one from 1 till 100. After counting we concluded that there are total 100 numbers from 1 to 100.
What are Whole Numbers in Math?
In Math, the set of positive integers and 0 is termed whole numbers. We can also say that the whole numbers are a set of natural numbers and 0. The set of whole numbers is represented as W = 0,1,2, 3, 4,.... and so on.
How to Write the Number 100 in Words?
The number 100 in words is written as Hundred.
What are the First Five Natural Numbers?
The first five natural numbers are 1, 2, 3, 4, and 5. In math, the numbers are classified into various forms. Natural numbers are one of the basic forms of numbers. Natural numbers are used for counting and are also considered as a part of real numbers. In words, the first five natural numbers are written as one, two, three, four, and five.
What are the Roman Numbers in Maths?
Roman numerals form a number system that is used to represent a numeric value in the form of letters. There are seven special letters to represent different numbers. These special letters are I, V, X, L, C, D, and M. Each letter amongst the seven special letters holds numeric values such as 1, 5, 10, 50, 100, 500, and 1000 respectively. The first ten roman numbers are I (one), two (II), three (III), four (IV), five (V).
What are the Properties of Numbers?
Some of the important properties of numbers are:
- Commutative Property: This property of numbers is applicable to addition and multiplication. It is expressed as, a + b = b + a and a × b = b × a.
- Associative Property: This property of numbers is applicable to addition and multiplication. It is expressed as, a + (b + c) = (a + b) + c and a × (b × c) = (a × b) × c.
- Distributive Property: The product of the sum of two numbers and a third number is equal to the sum of the product of each addend and the third number. It is expressed as a × (b + c) = a × b + a × c.
- Identity Property: We have an additive identity equal to 0 and a multiplicative identity equal to 1. It is written as, a + 0 = a and a × 1 = a.
- Reflexive Property: This property implies that every number is equal to itself. It is written as, for all a, a = a.
- Symmetric Property: If a number x is equal to y, then y is equal to x. It can be written as, x = y ⇒ y = x.
- Transitive Property: If x is equal to y and y is equal to z, then we can say that x = z. It is expressed as, x = y and y = z ⇒ x = z.
- Inverse Property: When an arithmetic operation is applied between a number and its inverse, we can get the identity. It is expressed as, a + (-a) = 0 and a × (1/a) = 1.
What are the Different Types of Numbers in Maths?
There are different types of numbers in Maths. They can be listed as follows:
visual curriculum