Number Line
A number line is a visual representation of numbers on a straight line. This line is used to compare numbers that are placed at equal intervals on an infinite line that extends on both sides, horizontally or vertically. As we move towards the right side of a horizontal number line, the numbers increase; as we move towards the left, the numbers decrease.
| 1. | What is a Number Line? |
| 2. | Negative and Positive Number Line |
| 3. | Number Line with Decimals |
| 4. | Inequalities on a Number Line |
| 5. | FAQs on Number Line |
What is a Number Line?
A visual representation of numbers on a straight line drawn either horizontally or vertically is known as a number line. Writing down numbers on a number line makes it easy for us to compare them and to perform basic arithmetic operations on them. Zero (0) is considered to be the origin of a number line. The numbers to the left of 0 are negative numbers and the numbers to the right of 0 are all positive numbers. So, we can say that on a number line, as we move towards the right, the value of numbers increases. This means that the numbers present on the right are larger than the numbers on the left. For example, 3 comes to the right of 1, so 3 > 1. Observe the horizontal number line given below.

How to Draw a Number Line?
In order to draw a number line or to plot a number on it, we use the following steps.
- Step 1: Draw a horizontal line with arrows on both ends. (You can also draw a vertical number line)
- Step 2: Choose a scale depending on the given number. For example, if you have to plot 5, then you can choose a scale of 1. If you have to plot 50, you can choose a scale of either 5, 10, or 25. (Determining an appropriate scale depends on the factors of the given number)
- Step 3: Mark the points at equal intervals. So, if you have chosen 1 as the scale, then mark 0, 1, 2, 3, 4, and so on.
- Step 4: Locate the given number. Highlight that point with a circle.
Negative and Positive Number Line
As we discussed above, a number line has positive and negative numbers. The section of the number line to the left side of zero forms a negative number line. While, the section on the right side of zero contains all positive numbers, and it forms a positive number line. It can be extended to infinity from both ends (right and left). The parts of a number line and some of its properties are given below.
Parts of a Number Line
Observe the parts of a number line given below to relate to the following features of a number line.
- The numbers on the right side are greater than the numbers on their left.
- The numbers on the left side are smaller than the numbers on their right.
- 0 is the point of origin or the middle point of the number line.
- Numbers are always placed at equal intervals in a number line.

Number Line with Decimals
We can represent various types of numbers on a number line, such as whole numbers, fractions, decimals, integers, rational numbers, and even irrational numbers. Now, let us learn how to draw a number line with decimals. For example, let us represent 2.4 on a number line using the steps given below:
- Step 1: Identify the whole number part of the given decimal. Here, in 2.4, the whole number part is 2.
- Step 2: Now, draw a number line and mark two points on it with a suitable gap in between. Since 2.4 lies between 2 and 3, mark 2 and 3 on the number line as shown below.
- Step 3: Observe the digit after the decimal, that is, the digit in the tenths place digit of the given number. In 2.4, the tenths place digit is 4. Make 10 equal intervals between 2 and 3 and mark 2.4 on the fourth bar to the right of 2.

This is how we draw a number line with decimals.
Inequalities on a Number Line
Inequality is a mathematical statement used for the comparison of quantities. We can graph inequalities on a number line by marking the part that the inequality represents.
Graphing Inequalities on a Number Line
Let us learn how to graph inequalities on a number line. Observe the figure given below that represents the following inequalities on a number line: x ≥ 5, x > 5, x ≤ 5, and x < 5.
Example 1: Represent x ≥ 5 on a number line.
Solution: In order to represent x ≥ 5 on a number line, we can follow the steps given below:
- Step 1: Draw a number line of a suitable length, mark 0, and draw equal intervals to the right and left, as shown in the figure given below.
- Step 2: In the given inequality x ≥ 5, the value of x can be 5 or greater than 5. So, we need to move to the right of 5.
- Step 3: Mark a black filled circle on 5 and shade the line from 5 towards the right side until the arrow as shown in the following figure.
- Step 5: This mark will represent the required inequality on the number line.
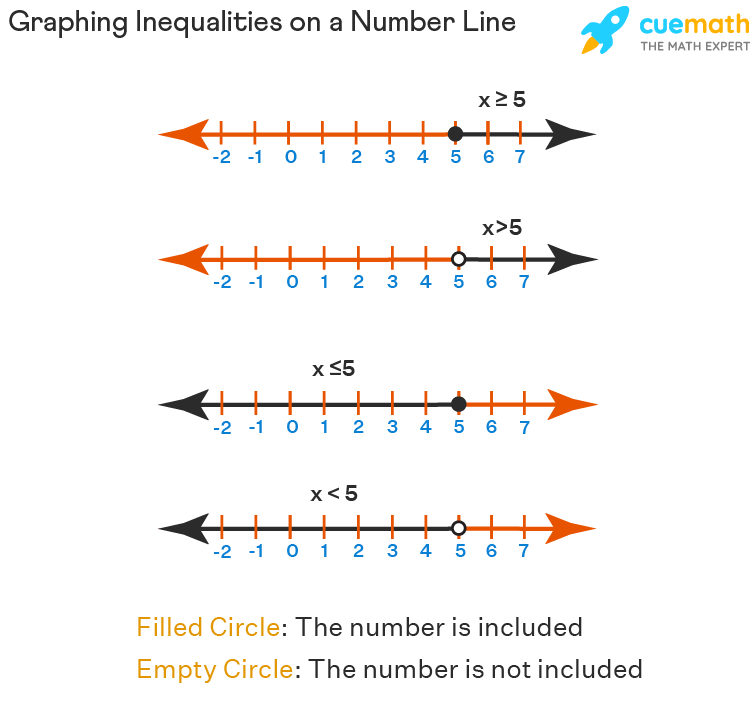
Note: It is to be noted that if the inequality says that the number is included, then we mark a filled circle on the particular number, whereas, if the inequality says that the number is not included then we mark an empty circle on the number. In the above case, it says that x is greater than or equal to 5, so we will mark a filled circle on 5.
Example 2: Represent x > 5 on a number line.
Solution: In order to represent x > 5 on a number line, we will follow the steps given below:
- Step 1: Draw a number line, mark 0, and draw equal intervals to the right and left, as shown in the figure given above.
- Step 2: In the given inequality x > 5, the value of x is greater than 5. So, we need to move to the right of 5.
- Step 3: Mark a black empty circle on 5 and shade the line from 5 towards the right side until the arrow as shown in the figure. The circle at point 5 will be left empty because a blank circle shows that 5 is not included. This means that x is greater than 5 and not equal to 5.
- Step 5: This mark will represent the required inequality on the number line.
Example 3: Represent x ≤ 5 on a number line.
Solution: In order to represent x ≤ 5 on a number line, we will follow the steps given below:
- Step 1: Draw a number line, mark 0, and draw equal intervals to the right and left, as shown in the figure given above.
- Step 2: In the given inequality x ≤ 5, the value of x is less than or equal to 5. So, we need to move to the left of 5.
- Step 3: Mark a black filled circle on 5 and shade the line from 5 towards the left side until the arrow as shown in the figure. The circle at point 5 will be filled because a filled circle shows that 5 is also included. This means that x is less than 5 or equal to 5.
- Step 5: This mark will represent the required inequality on the number line.
Example 4: Represent x < 5 on a number line.
Solution: In order to represent x < 5 on a number line, we will follow the steps given below.
- Step 1: Draw a number line, mark 0, and draw equal intervals to the right and left, as shown in the figure given above.
- Step 2: In the given inequality x < 5, the value of x is less than 5. So, we need to move to the left of 5.
- Step 3: Mark a black empty circle on 5 and shade the line from 5 towards the left side until the arrow as shown in the figure. The circle at point 5 will be left empty because a blank circle shows that 5 is not included. This means that x is less than 5 and not equal to 5.
- Step 5: This mark will represent the required inequality on the number line.
Tips and Tricks on Number line
- We can represent various numbers on the number line, according to our requirements. For example, they can be only positive numbers, or integers between -4 and 3, or even fractions between -2 and 2.
- Number lines can help us in real-life situations. For example, they read the altitude (height) which is shown on a GPS device's screen, and can tell you how high or low you are below sea level!
☛ Related Topics
Number Line Examples
-
Example 1: A flower is hidden behind an integer which is at a position 7 less than the spot where the butterfly is placed. Can you find the integer?

Solution:
From the above number line, it is clear that the butterfly is placed at 4. Now, 7 steps less than 4 means that 7 steps to the left of number 4 will take the butterfly to the flower. This can also be understood as: + 4 − 7 = −3.
This brings us to -3.
Thus, the flower is hidden behind -3.
∴ The integer is -3.

-
Example 2: Show the following addition on a number line.

Solution:
To perform addition on a number line we first look for the numbers from where we have to start. Here, the starting number is 300 and we need to add 500 to it. The addition of 300 + 500 is shown in the following number line:

-
Example 3: Represent y ≥ 2 on a number line.
Solution:
y ≥ 2 means that the value of a variable y is 2 or greater than 2. This can be easily represented on the number line as:

The black region on the line represents y ≥ 2.

FAQs on Number Line
What is a Number Line in Math?
A number line is a visual representation of numbers on a straight line. This line is used to compare numbers that are placed at equal intervals on an infinite line that extends on both sides, horizontally or vertically.
What is a Number Line Model?
A number line model is a representation of numbers plotted on an infinite line that extends at both ends.
What all Operations can be Performed Using Number Line?
The four basic arithmetic operations of addition, subtraction, multiplication, and division can be easily performed using a number line. For addition and multiplication, we move towards the right side and for subtraction, we move towards the left side of the number line.
What all Numbers can be Represented on a Number Line?
We can represent real numbers on the number line. It includes the set of whole numbers, integers, fractions, decimals, rational and irrational numbers.
How to Perform Addition Using Number Line?
When we perform addition on a number line, we count by moving one interval at a time towards the right side. For example, if we need to solve 4 + 5, we start by marking the number 4 on the number line. Since we are adding 4 and 5, we will move 5 steps to the right. This brings us to 9. Hence, 4 + 5 = 9.
How to Graph an Inequality on a Number Line?
We can easily graph inequalities on a number line. For this, we just need to circle the value and shade the appropriate region on the number line. For example, let us represent x > 7 on the number line using the following steps:
- Step 1: Draw a number line and locate point 7 on it with respect to the origin.
- Step 2: Then, mark an empty circle at point 7 and shade the region to the right of 7 on the number line because we need to represent the part that is greater than 7.
- Step 3: This will represent that x can be any value greater than 7.
- Step 4: Make sure that you mark a blank circle at point 7. A blank (empty) circle shows that the given number is not included.
- Step 5: In case we need to show x ≥ 7, we will mark a filled circle on 7. A filled circle shows that 7 is also included, that is, the value of x is equal to and greater than 7.
(For more details, read the section 'Inequalities on a Number Line' on this page.)
How to Represent Fractions on a Number Line?
In order to represent fractions on a number line, we find two whole numbers between which the fraction lies. Then, we make equal intervals between those two whole numbers and appropriately mark the given fraction.
How to Represent Rational Numbers on Number Line?
In order to represent rational numbers on the number line, we locate two integers between which the number is lying. Then we mark the point by making equal intervals between those two points. If the rational number is in the form of an integer, then we can simply locate the point with respect to the origin and mark it.
What is an Open Number Line?
An open number line is an empty number line in which the numbers are not marked. It is used to create a visual model according to our requirement and convenience so that we can perform different arithmetic operations like addition and subtraction on a number line.
What is a Double Number Line?
Double number lines consist of 2 number lines that have corresponding pairs of values marked on them. Double number lines are commonly used to compare 2 quantities or ratios which represent a relationship. For example, the scale on a map is a double number line that shows the distance given in centimeters and the corresponding distance in kilometers.
Why are Number Lines Important?
Number lines are important because they make us visualize the position and order of all real numbers including positive numbers and negative numbers. They also help in understanding the basics of addition and subtraction.
visual curriculum