Factors

The factor of a number, in math, is a divisor of the given number that divides it completely, without leaving any remainder. In order to find the factors of a number, we can use different methods like the division method and the multiplication method. Factors are used in real-life situations when we need to divide something into equal rows and columns, compare prices, exchange money, and so on. Let us learn more about factors and how to find the factors of a number in this article.

1.	What are Factors?
2.	Properties of Factors
3.	How to Find the Factors of a Number?
4.	Finding the Number of Factors
5.	FAQs on Fractions

In math, a factor is a number that divides another number completely with no remainder. Factors and multiples are a part of our daily life. For example, they are used in arranging items in a box, handling money, finding patterns in numbers, solving ratios, and working with expanding or reducing fractions.

Factor Definition

The factor of a number is a number that divides the given number completely without any remainder. The factors of a number can be positive or negative. For example, let us find the factors of 8. Since 8 is divisible by 1, 2, 4, and 8, we can list the positive factors of 8 as, 1, 2, 4, and 8. Apart from this, 8 has negative factors as well, which can be listed as, -1, -2, -4, -8 because the product of two negative numbers is a positive number, which means (-1) × (-8) = 8, and (-2) × (-4) = 8. However, we commonly use only the positive factors of a number. Let us read about a few properties of factors.

The factors of a number have the following properties:

• The number of factors of a number is finite.
• The factor of a number is always less than or equal to the given number.
• Every number except 0 and 1 has at least two factors, 1 and the number itself.
• Division and multiplication are the operations that are used in finding the factors of a number.

In order to find the factors of a number, we can use the division method and the multiplication method. Let us read about these methods in the following sections.

Finding Factors using Division Method

Let us find the factors of a number using the division method.

Example: Find the factors of 12 using the division method.

Solution: Let us find the factors of 12 using the following steps.

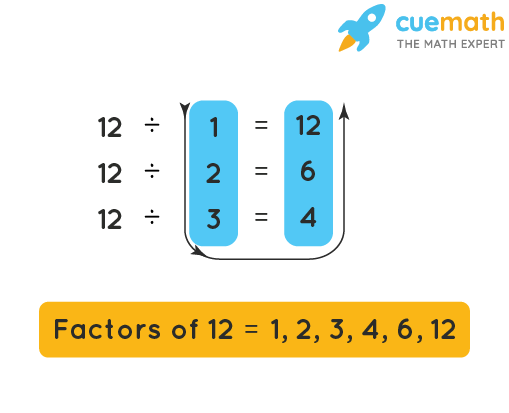
• Step 1: In order to find the factors of 12 using the division method, we need to check what numbers completely divide 12. We start checking from 1 and go on till 9. We need to make a note of those numbers that divide 12 completely.
• Step 2: The numbers that completely divide 12 are known as its factors. We write that particular number along with its pair and make a list as shown in the figure given above. As we check and list all the numbers up to 9, we automatically get the other pair factor along with it. For example, starting from 1, we write 12 ÷ 1 = 12, and 12 ÷ 2 = 6 and so on. Here, the divisor and the quotient are the factors of the number. This means (1, 12) forms the first pair, (2, 6) forms the second pair and the list goes on as shown. So, as we write 1 as the factor of 12, we get the other factor as 12; and as we write 2 as the factor of 12, we get 6 as the other factor. Like this, we get all the factors.
• Step 3: After the list is noted, we get all the factors of 12 starting from 1 up there, coming down and then we go up again up to 12. This gives us a complete list of all the factors of 12 as shown in the figure given above.

Therefore, the factors of 12 can be listed as 1, 2, 3, 4, 6, 12.

Now, let us learn how to find the factors of a number using the multiplication method. It is almost the same as the division method, the only difference is that the factors are written in different places.

Finding Factors using Multiplication Method

In order to find the factors of a number using the multiplication method, we need to use a similar procedure as given above except for a few changes. Let us learn this method with the help of an example.

Example: Find the factors of 24 using the multiplication method.

Solution: Let us find the factors of 24 by multiplication method using the following steps.

• Step 1: In order to find the factors of 24 using multiplication, we need to check what pairs of numbers multiply to give us 24, so we need to divide 24 by natural numbers starting from 1 and go on till 9.
• Step 2: We write that particular number along with its pair and make a list as shown in the figure given above. As we check and list all the numbers up to 9, we automatically get the other pair factor along with it. For example, starting from 1, we write 1 × 24 = 24 and 2 × 12 = 24 and so on. Here, (1, 24) forms the first pair, (2, 12) forms the second pair and the list goes on as shown. So, as we write 1 as the factor of 24, we get the other factor as 24; and as we write 2 as the factor of 24, we get 12 as the other factor. In this way, we get all the factors.
• Step 3: After the list is noted, we get all the factors of 24 starting from 1 up there, coming down and then we go up again up to 24. This gives us a complete list of all the factors of 24 as shown in the figure given above.

Therefore, the factors of 24 can be listed as 1, 2, 3, 4, 6, 8, 12, and 24.

We can find the number of factors of a given number using the following steps.

• Step 1: Do the prime factorization of the given number, i.e., express it as the product of primes.
• Step 3: Write the prime factorization in the exponent form.
• Step 3: Add 1 to each of the exponents.
• Step 4: Multiply all the resultant numbers. This product gives the number of factors of the given number.

Example: Find the number of factors of the number 108.

Solution: Let us find the number of factors of 108 using the steps given below.

• Step 1: The prime factorization of the number 108 gives us 108 = 2 × 2 × 3 × 3 × 3
• Step 2: After writing the prime factorization in the exponent form we get, 108 = 2² × 3³
• Step 3: After adding 1 to each of the exponents, 2 and 3 we get (2 + 1) = 3, (3 + 1) = 4.
• Step 4: Now let us multiply these numbers: 3 × 4 = 12. Therefore, the number of factors of 108 is 12.

We can verify this number by writing the actual factors of 108 which are 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, and 108. Here, 108 has 12 factors, hence, we have verified that 108 has 12 factors.

Factors of Numbers

Here is a list of the pages that explain the factors of different numbers.

Factors of 2 Factors of 4 Factors of 5 Factors of 6 Factors of 7 Factors of 8 Factors of 9 Factors of 10 Factors of 11 Factors of 12 Factors of 13 Factors of 14 Factors of 15 Factors of 16 Factors of 17 Factors of 19 Factors of 20 Factors of 21 Factors of 22 Factors of 23 Factors of 24 Factors of 25 Factors of 26 Factors of 27 Factors of 28 Factors of 29 Factors of 30 Factors of 31 Factors of 32 Factors of 33 Factors of 34 Factors of 35 Factors of 37 Factors of 38 Factors of 39 Factors of 40

Factors of 41 Factors of 42 Factors of 43 Factors of 44 Factors of 46 Factors of 47 Factors of 48 Factors of 49 Factors of 50 Factors of 51 Factors of 52 Factors of 53 Factors of 54 Factors of 55 Factors of 56 Factors of 57 Factors of 58 Factors of 59 Factors of 61 Factors of 62 Factors of 63 Factors of 65 Factors of 66 Factors of 67 Factors of 68 Factors of 69 Factors of 70 Factors of 71 Factors of 72 Factors of 73 Factors of 74 Factors of 75 Factors of 76 Factors of 77 Factors of 78 Factors of 79

Factors of 80 Factors of 81 Factors of 84 Factors of 85 Factors of 86 Factors of 87 Factors of 88 Factors of 89 Factors of 90 Factors of 91 Factors of 92 Factors of 93 Factors of 96 Factors of 97 Factors of 98 Factors of 99 Factors of 104 Factors of 105 Factors of 108 Factors of 112 Factors of 117 Factors of 119 Factors of 121 Factors of 125 Factors of 128 Factors of 135 Factors of 140 Factors of 144 Factors of 147 Factors of 150 Factors of 160 Factors of 168 Factors of 175 Factors of 180 Factors of 192 Factors of 200

Factors of 216 Factors of 224 Factors of 243 Factors of 245 Factors of 250 Factors of 256 Factors of 270 Factors of 288 Factors of 294 Factors of 300 Factors of 320 Factors of 360 Factors of 400 Factors of 441 Factors of 450 Factors of 512 Factors of 625

 

What are Factors in Math?

A factor is a number that divides the given number without any remainder. The factors of a number can either be positive or negative. The factors of any number are finite. For example, the factors of 7 are 1 and 7. The factors of 8 are 1, 2, 4, and 8.

How to Find the Number of Factors of a Number?

We can find the number of factors of a given number using the following steps. Let us understand this with the help of an example and find the number of factors of 48

• Step 1: Do the prime factorization of the given number. This will be 48 = 2 × 2 × 2 × 2 × 3
• Step 3: Write the prime factorization in the exponent form. This can be written as 2⁴ × 3¹
• Step 3: Add 1 to each of the exponents. The exponents, in this case, are 4 and 1. So, after adding 1 to each exponent, we get 5 and 2.
• Step 4: Multiply the resultant numbers. This product gives the number of factors of the given number. After multiplying 5 × 2 = 10. This means 48 has 10 factors. Let us verify this by listing the factors of 48. Factors of 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 48.

What is Prime Factorization?

Prime factorization of a number is a way of expressing the number as a product of its prime factors. For example, the prime factorization of 60 = 2 × 2 × 3 × 5. The prime factorization of a number always shows its prime factors. In this case, 2, 2, 3 and 5 are the prime factors of 60. We know that prime factors are those factors that are prime numbers.

What is the Factors Formula?

The factors formula for a number gives the total number of factors of a number. For a number N, whose prime factorization is X^a × Y^b, we get the total number of factors by adding 1 to each exponent and then multiplying these together. This expresses the number of factors formula as, (a + 1) × (b + 1), where a, and b are the exponents obtained after the prime factorization of the given number. For example, let us find the total number of factors of the number 12. The prime factorization of 12 = 2 × 2 × 3. This can be written in the exponent form as 2² × 3¹. Let us use the formula, (a + 1) × (b + 1) where a and b are 2 and 1 respectively. After substituting the values we get, (a + 1) × (b + 1) = (2 + 1) × (1 + 1) = 3 × 2 = 6. This means 12 has 6 factors in all. This can be verified by listing the factors of 12 which are, 1, 2, 3, 4, 6, 12.

What are the Common Factors of 4 and 12?

The factors of 4 are 1, 2, and 4. The factors of 12 are 1, 2, 3, 4, 6, and 12. Therefore, it can be seen that the common factors of 4 and 12 are 1, 2, and 4.

What Number is a Factor of Each Number?

1 is a factor of each number because 1 divides every number completely.

What are the Prime Factors of a Number?

The prime factor of a number is the factor which is a prime number. For example, the prime factors of 12 are 2, 2, and 3 because 2 × 2 × 3 = 12. These prime factors when multiplied together give the product as the number. The prime factors of a number can be calculated using the factor tree method or the division method.

Can Factors be Negative?

Yes, the factors of a number can be negative because we know that the product of two negative numbers is a positive number. For example, if we multiply (-2) × (-3), we get 6. Similarly, (-1) × (-6) = 6. This means that -1, -2, -3 and -6 are the negative factors of 6. This shows that a number can have positive and negative factors. In this case, the positive factors of 6 can be listed as 1, 2, 3, and 6; and the negative factors of 6 can be listed as -1, -2, -3, and -6.