Factors of 75
Factors of 75 are the list of integers that can be evenly divided into 75. Negative factors of 75 are just factors with a negative sign. Did you know that the number of balls in a standard game of Bingo played in the United States is 75? In this lesson, we will find the factors of 75 its prime factors, and its factors in pairs. We will also go through some solved examples to understand the factors of 75.
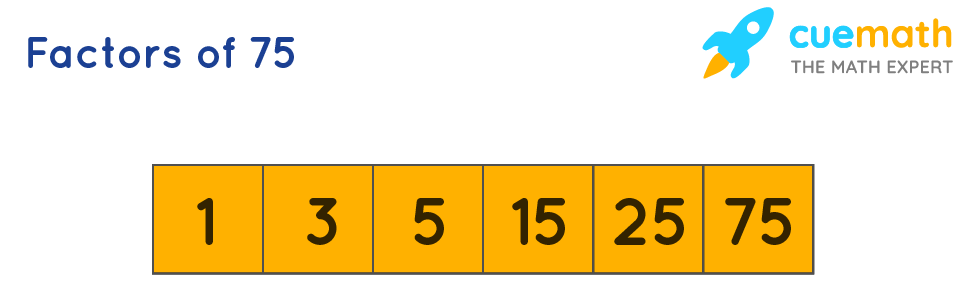
- Factors of 75: 1, 3, 5, 15, 25 and 75
- Factors of -75: -1, -3, -5, -15, -25, -75
- Prime Factorization of 75: 75 = 3 × 52
| 1. | What are Factors of 75? |
| 2. | How to Calculate the Factors of 75 |
| 3. | Factors of 75 by Prime Factorization |
| 4. | Factors of 75 in Pairs |
| 5. | Important Notes |
| 6. | FAQs on Factors of 75 |
What are Factors of 75?
Factors of 75 are the numbers which when multiplied in pairs give the product as 75. Factors of a number n are the numbers that completely divide the number n. It means that if the remainder in n/a is zero, then a is the factor of n.

In this topic, we will find the factors of the number 75. Let's first see the numbers that completely divide 75. The numbers that divide 75 completely are 1, 3, 5, 15, 25, and 75.

Hence, the factors of 75 are 1, 3, 5, 15, 25, and 75.
How to Calculate Factors of 75?
The factors of a number can be calculated using several methods; one of the methods involves dividing the number by the smallest of the factors. Factors of number 75 can be calculated as follows:
- Step 1: write the smallest factor of 75 (except 1). The smallest factor of 75 is 3
- Step 2: Divide 75 by 3 i.e. 75/3 = 25. Hence, 3 and 25 are the factors of 75
- Step 3: write the next smallest factor of 75. The next smallest factor of 75 is 5. Divide 75 by 5 i.e. 75/5 = 15. Hence, 5 and 15 are the factors of 75
- Step 4: Include 1 and the number itself while writing all the factors.
Thus, the factors of 75 are 1, 3, 5, 15, 25, and 75. Explore factors of other numbers using illustrations and interactive examples:
- Factors of 175 - The factors of 175 are 1, 5, 7, 25, 35, 175
- Factors of 15 - The factors of 15 are 1, 3, 5, 15
- Factors of 25 - The factors of 25 are 1, 5, 25
- Factors of 35 - The factors of 35 are 1, 5, 7, 35
- Factors of 63 - The factors of 63 are 1, 3, 7, 9, 21, 63
- Factors of 54 - The factors of 54 are 1, 2, 3, 6, 9, 18, 27, 54
Factors of 75 by Prime Factorization
The prime factorization method to calculate the factors of any number is one of the most important methods. Many students prefer using prime factorization while performing calculations. In the prime factorization method, we can only factorize a number into its prime factors.
Prime Numbers: Prime numbers are the numbers that have only two factors - 1 and the number itself. For example, 2, 3, 5, 7, 11, 13 are prime numbers.

Prime Factors of 75
Prime factors of 75 are: 75 = 3 × 5 × 5. Let's write all the factors of 75 using prime factors
- Step 1: Take all the numbers and multiply only two at a time. 3, 5, 5
- Step 2: Multiply each number with another number once. i.e. 3 × 5 = 15 and 5 × 5 = 25. Therefore, factors obtained are 15, 25
- Step 3: Write all the factors of the number i.e. 1, 3, 5, 15, 25, 75
Now that we have done the prime factorization of 75, we can multiply them and get the other factors. Can you try and find out if all the factors are covered or not? And as you might have already guessed, for prime numbers, there are no other factors.
Factors of 75 in Pairs
The pair of factors of number n is the set of two numbers which when multiplied together gives the number n. Factors of 75 are: 1, 3, 5, 15, 25, 75 and Pair factors of 75 are: (1, 75), (3, 25), (5, 15).
- 1 × 75 = 75
- 3 × 25 = 75
- 5 × 15 = 75

Negative factors of 75 are: -1, -3, -5, -15, -25, -75 and pairs of negative factors of 75 are: (-1, -75), (-3, -25), (-5, -15)
- -1 × -75 = 75
- -3 × -25 = 75
- -5 × -15 = 75

Try finding the pair factors of 15 and the pair factors of 25.
Factors of 15 are: 1, 3, 5, 15 and pairs of factors of 15 are: (1, 15), (3, 5)
i.e. 1 × 15 = 15 and 3 × 5 = 15
Factors of 25 are: 1, 5, 25 and Pairs of factors of 25 are: (1, 25), (5, 5)
i.e. 1 × 25 = 25 and 5 × 5 = 25
Important Notes:
- The prime factors of a number are different from their factors.
- If a number n has an odd number of positive factors, then n is a perfect square.
- 1 and the number itself are the factors of any number.
- There are no factors of a number n between (n, n/2).
- A number that has more than 2 factors is called a composite number.
- 1 is not a prime number; 2 is the smallest prime number.
Factors of 75 Solved Examples
-
Example 1: Help Donald find the sum of all the positive factors of 75.
Solution:
Positive factors of 75 are 1, 3, 5, 15, 25, 75. The sum of all the factors is 1 + 3 + 5 + 15 + 25 + 75 = 124
Hence, the sum of all the positive factors of 75 is 124.
-
Example 2: Find the largest number which can divide 300, 275, and 325.
Solution:
To find the largest number which can divide 300, 275, and 325, we need to calculate the HCF of these numbers.
- 300 = 1 × 2 × 2 × 3 × 5 × 5
- 275 = 1 × 5 × 5 × 11
- 325 = 1 × 5 × 5 × 13
HCF of 300, 275, and 325 is 1 × 5 × 5 = 25. Hence, 25 is the largest number which can divide 300, 275, and 325.
-
Example 3: Julia wants to add a natural number to 10 so that it will become a factor of 75. What number should be added?
Solution:
Let's assume that she adds x to 10. Hence, x + 10 is a factor of 75. Let's write down all the factors of 75 greater than 10: 15, 25, 75
Hence, x can be 5, 15, 65. Thus, Julia can add 5, 15, and 65 to 10 so that it will become a factor of 75.
- x + 10 = 15
- x + 10 = 25
- x + 10 = 75

FAQs on Factors of 75
What are all the Factors of 75?
The factors of 75 are 1, 3, 5, 15, 25, and 75.
What are all the Factors of 76?
The factors of 76 are 1, 2, 4, 19, 38, and 76.
Is 75 a Prime Number?
75 is not a prime number because it has more than two positive factors.
Is 75 a Perfect Square?
75 is not a perfect square because 75 has an even number of positive factors and √75 = 8.66
What are the Common Factors of 75 and 100?
The factors of 75 are 1, 3, 5, 15, 25, 75 and the factors of 100 are 1, 2, 4, 5, 10, 20, 25, 50, 100. Hence, the common factors are 1, 5, 25.
visual curriculum