Factors of 30
Factors of 30 are numbers that, when multiplied in pairs give the product as 30. There are overall 8 factors of 30 among which 30 is the biggest factor and 1, 2, 3, 5, 6, 10, 15, and 30 are positive factors. The sum of all factors of 30 is 72. Its Prime Factors are 1, 2, 3, 5, 6, 10, 15, 30 and (1, 30), (2, 15), (3, 10) and (5, 6) are Pair Factors.
- Factors of 30: 1, 2, 3, 5, 6, 10, 15 and 30
- Negative Factors of 30: -1, -2, -3, -5, -6, -10, -15 and -30
- Prime Factors of 30: 2, 3, 5
- Prime Factorization of 30: 2 × 3 × 5 = 2 × 3 × 5
- Sum of Factors of 30: 72
| 1. | What are Factors of 30? |
| 2. | How to Calculate Factors of 30? |
| 3. | Factors of 30 by Prime Factorization |
| 4. | Factors of 30 in Pairs |
| 5. | Important Notes |
| 6. | FAQs on Factors of 30 |
What are Factors of 30?
The factors of 30 are all the integers that 30 can be divided into. The number 30 is an even composite number. A number is said to be composite if it has more than two factors. Since it is even, it will have 2 as a factor. Thus, by understanding the properties of the number 30, we can find the factors of 30 which are 1, 2, 3, 5, 6, 10, 15, and 30.

Explore factors using illustrations and interactive examples:
- Factors of 360: The factors of 360 are 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180 and 360.
- Factors of 24: The factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24.
- Factors of 6: The factors of 6 are 1, 2, 3, and 6.
- Factors of 180: The factors of 180 are 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, and 180.
- Factors of 45: The factors of 45 are 1, 3, 5, 9, 15, and 45.
How To Calculate Factors of 30?
- Step 1: Let's begin calculating the factors of 30 with the idea that any number that completely divides 30 without any remainder is its factor.
- Step 2: Let's start with the whole number 1. We know that 30 ÷ 1 = 30
- Step 3: The next whole number is 2. Now, divide 30 by 2. Thus, 30 ÷ 2 = 15.
- Step 4: Proceeding in this manner we get, 30 ÷ 3 = 10 and 30 ÷ 5 = 6. In this way, we can obtain all the factors of 30.
- Step 5: All these numbers when multiplied make up the factors of 30. That is 30 = 1 × 30, 2 × 15, 3 × 10 and 5 × 6.
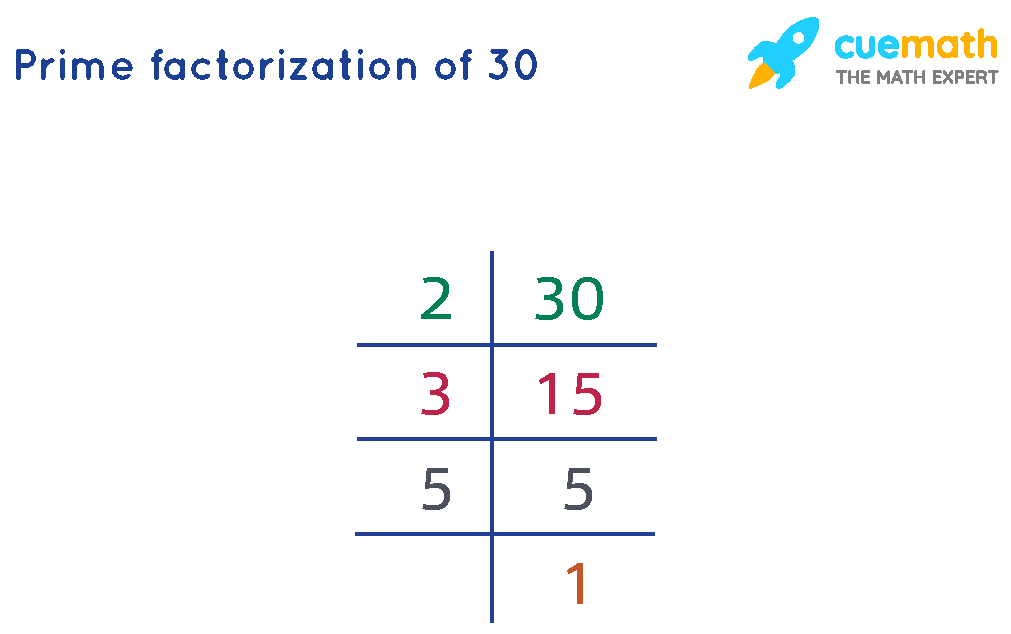
Factors of 30 by Prime Factorization
Prime factorization is to express a composite number as the product of its prime factors.
- Step 1: To get the prime factors of 30, we divide it by its smallest prime factor, which is 2. Thus, 30 ÷ 2 = 15.
- Step 2: Now, 15 is divided by its smallest prime factor and the quotient is obtained. We get 15 ÷ 3 = 5
- Step 3: This process goes on until we get the quotient as 1.
The prime factorization of 30 is shown below:
Factors of 30 in Pairs
The pair of numbers that give 30 when multiplied is known as the factor pairs of 30. Following are the factors of 30 in pairs. Since 30 is positive, we have -ve × -ve = +ve.
| Product form of 30 | Pair factor |
| 1 × 30 = 30 | (1,30) |
| 2 × 15= 30 | (2,15) |
| 3 × 10 = 30 | (3,10) |
| 5 × 6 = 30 | (5,6) |
| -1 × -30 = 30 | (-1,-30) |
| -2 × -15 = 30 | (-2,-15) |
| -3 × -10 = 30 | (-3,-10) |
| -5 × -6 = 30 | (-5,-6) |
Important Notes
- As 30 ends with the digit 0, it will have 5 and 10 as its factors. This holds for all numbers that end with the digit 0.
- 30 is a non-perfect square number. Thus, it will have an even number of factors. This property holds for every non-perfect square number.
Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12. Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.
Factors of 30 Solved Examples
-
Example 1: Peter and Andrew both have rectangular papers with dimensions as shown below.

They place the two rectangles one over the other. Since the two shapes do not overlap, Peter informs Andrew that they don't have the same area. However, Andrew does not agree with him. Can you find out who is correct?
Solution:
Area of a rectangle = length × breadth. For the first rectangle, Area = 6 × 5 = 30 . For the second rectangle, Area = 10 × 3 = 30.
They have equal areas. Therefore, Andrew is correct as the two rectangles have equal areas.
-
Example 2: Jill has (-3) as one of the factors of 30. How will she get the other factor?
Solution:
30 = Factor 1 × Factor 2. We have 30 = (-3) × Factor 2, which means that Factor 2 = 30 ÷ (-3) =(-10).
Therefore, the other factor is -10.
-
Example 3: Find the Least Common Multiple and Greatest Common Factor (GCF) of 30 and 28.
Solution:
The factors of 30 are 1, 2, 3, 5, 6, 10, 15, 30 and factors of 28 are 1, 2, 4, 7, 14, 28.
Therefore, the Least Common Multiple of 30 and 28 is 420 and the Greatest Common Factor (GCF) of 30 and 28 is 2.

FAQs on Factors of 30
What are the Factors of 30?
The factors of 30 are 1, 2, 3, 5, 6, 10, 15, 30 and its negative factors are -1, -2, -3, -5, -6, -10, -15, -30.
What is the Greatest Common Factor of 30 and 6?
The factors of 30 and 6 are 1, 2, 3, 5, 6, 10, 15, 30 and 1, 2, 3, 6 respectively.
Common factors of 30 and 6 are [1, 2, 3, 6].
Hence, the Greatest Common Factor (GCF) of 30 and 6 is 6.
What are the Prime Factors of 30?
The prime factors of 30 are 2, 3, 5.
What are the Common Factors of 30 and 25?
Since, the factors of 30 are 1, 2, 3, 5, 6, 10, 15, 30 and the factors of 25 are 1, 5, 25.
Hence, [1, 5] are the common factors of 30 and 25.
What is the Sum of the Factors of 30?
Sum of all factors of 30 = (21 + 1 - 1)/(2 - 1) × (31 + 1 - 1)/(3 - 1) × (51 + 1 - 1)/(5 - 1) = 72
visual curriculum