Greatest Common Factor (GCF)
The GCF of two or more non-zero integers, x, and y, is the greatest positive integer m, which divides both x and y. The greatest common factor is commonly known as GCF. Here, greatest can be replaced with highest, and factor can be replaced with divisor. So, the greatest common factor is also known as Highest Common Divisor (HCD), Highest Common Factor (HCF), or Greatest Common Divisor (GCD).
GCF is used almost all the time with fractions, which are used a lot in everyday life. In order to simplify a fraction or a ratio, you can find the GCF of the denominator and numerator and get the required reduced form. Also, if we look around, the arrangement of something into rows and columns, distribution and grouping, all this require the understanding of GCF.
| 1. | What is Greatest Common Factor (GCF)? |
| 2. | How to Find GCF? |
| 3. | GCF and LCM |
| 4. | FAQs on GCF |
What is Greatest Common Factor (GCF)?
The GCF (Greatest Common Factor) of two or more numbers is the greatest number among all the common factors of the given numbers. The GCF of two natural numbers x and y is the largest possible number that divides both x and y without leaving any remainder. To calculate GCF, there are three common ways- division, multiplication, and prime factorization.
Example: Let us find the greatest common factor of 18 and 27.
Solution:
First, we list the factors of 18 and 27 and then we find out the common factors.
Factors of 18: 1, 2, 3, 6, 9, 18
Factors of 27: 1, 3, 9, 27
The common factors of 18 and 27 are 1, 3, and 9. Among these numbers, 9 is the greatest (largest) number. Thus, the GCF of 18 and 27 is 9. This is written as: GCF(18, 27) = 9.
A factor of a number is its divisor as well. Hence the greatest common factor is also called the Greatest Common Divisor (or) GCD. In the above example, the greatest common divisor (GCD) of 18 and 27 is 9 which can be written as:
GCD (18, 27) = 9.
How to Find GCF?
Following are the three methods for finding the greatest common factor of two numbers:
- Listing out common factors
- Prime factorization
- Division method
GCF by Listing Factors
In this method, factors of both the numbers can be listed, then it becomes easy to check for the common factors. By marking the common factors, we can choose the greatest one amongst all of them. Let's look at the example given below:
Example: What is the GCF of 30 and 42?
Solution:
- Step 1 - List out the factors of each number.
- Step 2 - Mark all the common factors.
- Step 3 - 6 is the common factor and the greatest one.
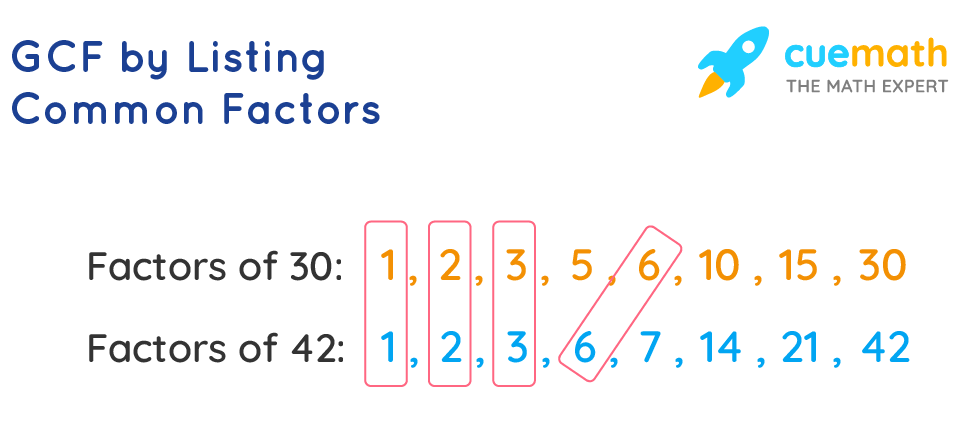
Therefore, GCF of 30 and 42 = 6. This method can be used for finding GCF of three or more numbers as well.
Finding the greatest common factor by listing factors may be difficult if the numbers are bigger. In such cases, we use the prime factorization and division methods for finding GCF.
GCF by Prime Factorization
Prime factorization is a way of expressing a number as a product of its prime factors, starting from the smallest prime factor of that number. Let's look at the example given below:
Example: What is the GCF of 60 and 90?
Solution:
- Step 1 - Represent the numbers in the prime factored form.
- Step 2 - GCF is the product of the factors that are common to each of the given numbers.

Thus, GCF (60,90) = 21 × 31× 51 = 30. Therefore, GCF of 60 and 90 = 30. We can also find the greatest common factor of three numbers or more by this method.
Finding GCF by Division Method
The division is a method of grouping objects in equal groups, whereas for large numbers we follow long division, which breaks down a division problem into a series of easier steps. The greatest common factor (GCF) of a set of whole numbers is the largest positive integer that divides all the given numbers, without leaving any remainder. Let's look at the example given below:
Example: Find the GCF of 198 and 360 using the division method.
Solution:
Among the given two numbers, 360 is the larger number and 198 is the smaller number.
- Step 1 - Divide the larger number by the smaller number using long division.
- Step 2 - If the remainder is 0, then the divisor is the GCF. If the remainder is not 0, then make the remainder of the above step as the divisor and the divisor of the above step as the dividend and perform long division again.
- Step 3 - If the remainder is 0, then the divisor of the last division is the GCF. If the remainder is not 0, then we have to repeat step 2 until we get the remainder 0.

Therefore, the GCF of the given two numbers is the divisor of the last division. In this case, the divisor of the last division is 18. Therefore, the GCF of 198 and 360 is 18. This method is the most appropriate method for finding GCF of large numbers. Let us see how to use the division method to find the greatest common factor of three numbers. In order to find the GCF of three numbers by long division, the following steps are to be followed:
- First, we will find the GCF of two of the numbers.
- Next, we will find the GCF of the third number and the GCF of the first two numbers.
Example: Find the GCF of 126, 162, and 180.
First, we will find the GCF of the two numbers 126 and 162. [You can choose any two numbers out of the given three numbers]

Thus, GCF of 126 and 162 = 18 ........(1).
Next, we will find the GCF of the third number, which is 180, and the above GCF 18 by using the same method.

Thus, GCF of 180 and 18 = 18 ......(2).
From (1) and (2), GCF(126, 162, 180) = 18. Therefore, GCF of 126, 162, and 180 = 18.
GCF and LCM
The greatest common factor is the largest number that divides the given numbers without leaving any remainder. On the other hand, the LCM (least common multiple) Is the smallest common multiple of the given numbers that can be divided by the given numbers exactly, without leaving a remainder. For example, let us find the GCF and LCM of numbers 6 and 8.
The factors of 6 are 1, 2, 3, 6, and the factors of 8 are 1, 2, 4, 8. So, the common factors of 6 and 8 are 1 and 2, out of which 2 is the highest common factor. Thus, GCF (6, 8) = 2. Now, the first few multiples of 6 are 6, 12, 18, 24, 30, ..., and the first few multiples of 8 are 8, 16, 24, 32, ... Out of these, the least common multiple of 6 and 8 is 24. Thus, LCM (6, 8) = 24.
One very interesting relation between GCF and LCM of two numbers is that the product of GCF and LCM of two numbers is equal to the product of the numbers. For any two numbers a and b, we have, LCM (a, b) × GCF (a, b) = a × b. Let us verify it using the above example of 6 and 8. Let a = 6 and b = 8.
LCM (6, 8) × GCF (6, 8) = 6 × 8
24 × 2 = 6 × 8
48 = 48
Hence verified.
Now, let us learn the difference between GCF and LCM in the section below.
Difference between GCF and LCM
The GCF or the greatest common factor of two or more numbers is the greatest factor among all the common factors of the given numbers, whereas the LCM or the least common multiple of two or more numbers is the smallest number among all common multiples of the given numbers. The following table shows the difference between GCF and LCM:
| Greatest Common Factor(GCF) | Least Common Multiple(LCM) |
|---|---|
|
The GCF of two natural numbers a and b is the greatest natural number x, which is a factor of both a and b. |
The LCM of two natural numbers a and b is the smallest number y, which is a multiple of both a and b. |
|
In the intersection of the sets of common factors, it is the greatest value. |
In the intersection of the sets of common multiples, it is the minimum value. |
| Represented as, GCF(a, b) = x |
Represented as, LCM(a, b) = y |
► Related Topics
Check these articles related to the concept of the greatest common factor (GCF) in math.
Greatest Common Factor Examples
-
Example 1: Find the GCF of 6, 12, and 36 by using the listing factors method.
Solution:
The given numbers are 6, 12, and 36. We will find the factors of each of these numbers. Then, circle the common factors.

In this example, 1, 2, 3, and 6 are all common factors of 6, 12, and 36. Out of all these common factors, 6 is the greatest, and hence, GCF(6,12,36) = 6.
-
Example 2: Find the GCF of 168, 252, and 288 by the prime factorization method.
Solution:
The given numbers are 168, 252, and 288. We will find the prime factorization of each of these numbers.

Thus, GCF (168,252,288) = 2 × 2 × 3 = 22 × 31. The GCF of these three numbers will be the product of the common prime factors of all three numbers. Thus, GCF of 168, 252 and 288 = 22 × 31 = 12.
-
Example 3: Find the GCF of 9000 and 980 using the division method.
Solution:
Among the given numbers, 9000 is the largest, and 980 is the smallest. We will divide the larger number by the smaller number. Next, we will make the remainder as the divisor and the last divisor as the dividend and divide again. We will repeat this process until the remainder is 0.

Therefore, the GCF of 9000 and 980 is 20.

FAQs on GCF
What is Meant by Greatest Common Factor (GCF)?
The greatest number among all the common factors of two or more numbers is called the greatest common factor or GCF. For any two numbers, the GCF is the largest number that divides the two given numbers. GCF can be calculated by using the basic arithmetic operations in mathematics i.e. division, multiplication, and prime factorization.
How to Find the Greatest Common Factor (GCF)?
To find the greatest common factor of two or more natural numbers, there are 3 methods that can be used - listing out of the common factors, prime factorization, and division method. Each method requires division and multiplication to obtain the GCF. For example, the GCF of 14 and 35 is 7. By using the listing common factors method, the factors of 14 are 1, 2, 7, 14 and the factors of 35 are 1, 5, 7, 35. The two common factors are 1 and 7 out of which 7 is the largest. Therefore, 7 is the GCF of 14 and 35.
What is the Greatest Common Factor of Two Prime Numbers?
A prime number has only two factors (1 and itself). Hence, two prime numbers cannot have any common factor other than 1. Therefore, the greatest common factor of two prime numbers is always 1. For example, the greatest common factor of 5 and 7 is 1.
What is the Greatest Common Factor of 24 and 54?
The factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24. The factors of 54 are 1, 2, 3, 6, 9, 18, 27, and 54. The common factors of 24 and 54 are 1, 2, 3, and 6. Hence, the GCF of 24 and 54 is 6.
What is the GCF of 15 and 20?
The factors of 15 are 1, 3, 5, and 15. The factors of 20 are 1, 2, 4, 5, 10, and 20. The common factors of 15 and 20 are 1 and 5. Thus, the GCF of 15 and 20 is 5.
How to Find GCF and LCM?
GCF (greatest common factor) and LCM (least common multiple) can be found by any of the methods written below:
- Listing method
- Prime factorization method
- Division method
All the methods are used differently for GCF ad LCM.
Are GCF and HCF the Same?
The greatest common factor is abbreviated as GCF and is also known as the Highest Common Factor (HCF). So, yes, GCF and HCF are the same.
Is GCF Greater Than LCM?
The LCM is the least common multiple of the given numbers that can be divided by both the numbers, while the GCF is the greatest common factor of the given numbers that divide both the numbers. Thus, for any two numbers, the LCM of the numbers is greater than the GCF of the numbers.
How to Find the Greatest Common Factor of a Polynomial?
The greatest common factor of a polynomial can be found by following the steps listed below:
- Step 1: Observe all the terms of the given polynomial carefully.
- Step 2: Find the numbers or variables that are common in all the terms.
That will be the required GCF of polynomial.
How do you Factor Out the GCF?
GCF of two or more numbers can be obtained by using the prime factorization method that is done only in a few steps. They are:
- List out the prime factors of all the numbers.
- Circle the common prime factors among all the numbers.
- Multiply all the circled numbers to find the GCF.
visual curriculum