Remainder
Remainder refers to the remaining part, after the completion of the division process. If we divide 5 pens among 4 children equally, we are left with 1 pen. This example is translated into math, the remaining 1 pen is the remainder. Also, if you divide the number 20, with a number 3, the quotient is 6 and the remainder is 2. The remainder is always lesser than the divisor.
In math, the remainder is something that is left over after the calculations. In numerous instances, the remainders are ignored or rounded, to give only a whole number answer. In the decimal number 5.02, the number 2 after the decimal is the remainder and is sometimes ignored to give only the whole number answer 5. Let us learn more about remainder and its use in Mathematics
| 1. | What is Remainder in Division? |
| 2. | Finding Remainder using Long Division? |
| 3. | How to Represent Remainder? |
| 4. | Properties of Remainder |
| 5. | FAQs on Remainder |
What is Remainder in Division?
The remainder, as its name suggests, is something that "remains" after completing a task. In math, the number 17 cannot be exactly divided by the number 3. After division, the number 2 is left aside as a remainder. As an example, let us assume that you have 15 cookies that you want to share with 3 of your friends, Mary, David, and Jake. You want to share the cookies equally among your friends and yourself. You will be distributing them in the following way.

Here, you can see that there are 3 cookies "remaining" after the distribution. These 3 cookies cannot be further shared equally among the 4 of you. Hence, 3 is called the "remainder". Also, on observation, the remaining 3 cookies are less in number than the 4 people, with whom the cookies have been shared. We can understand that the remainder is always lesser than the divisor.
Remainder Definition
Remainder is a part of a division. It is a left-over digit we get while performing division. When there is an incomplete division after certain steps we get remainder as a result. It is left over when a few things are divided into groups with an equal number of things. Let's recall the scenario we discussed earlier 15 cookies being shared equally among 4 children. In other words, 15 cookies had to be divided into 4 equal groups. We were left with 3 cookies and hence, 3 were the remainder.
Let us consider another example. Let us assume that 8 slices of pizza are to be shared equally among 2 children. How many pieces of pizza remain unshared? You can look at the picture below to understand how we have divided the slices of pizza equally between the two children. Thus, the remainder is 0 as no pieces of pizza are left unshared.
Finding Remainders Using Long Division
We cannot always pictorially show how we divide the number of things equally among the groups in order to find the remainder. Instead, we can find the remainder using the long division method. For example, the remainder in the above example on cookies can be found using long division as follows:
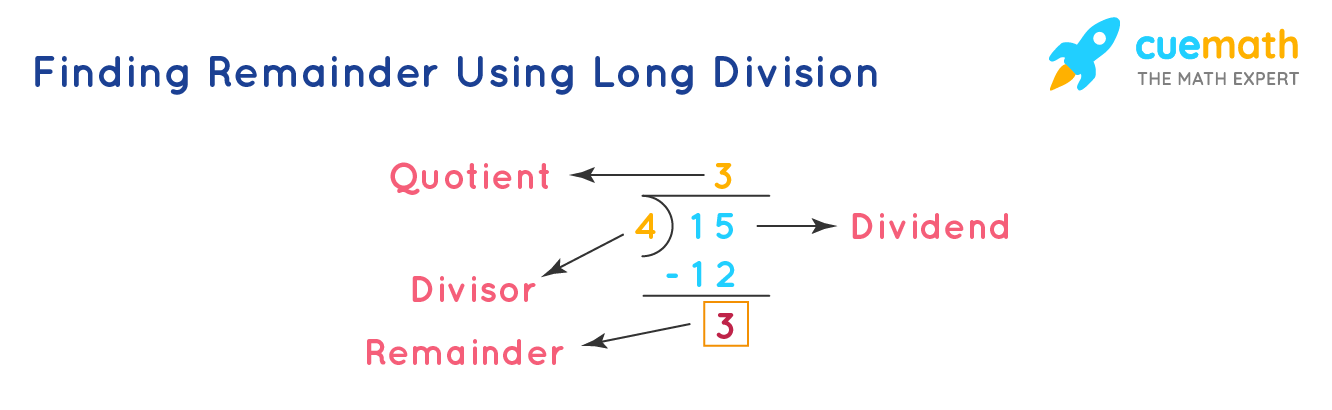
Thus, the remainder is 3. A remainder can also be a 0. The remainder on dividing 10 by 2, 18 by 3, or 35 by 7, is equal to 0. Here are some other examples of remainders.
| Division |
Remainder |
|---|---|
| 35/6 |
5 |
| 42/8 |
2 |
| 121/11 |
0 |
| 118/12 |
10 |
| 120/17 |
1 |
You can check these remainders by long division.
How to Represent Remainder?
Let us divide 7 by 2 using long division and see what the quotient and the remainder are. The quotient, divisor, the remainder can be together written as a mixed fraction to represent the dividend. The remainder forms the numerator of the mixed fraction, the divisor forms the denominator, and the quotient form the whole number part of the mixed fraction.

We can represent the remainder of the division in two ways.
- One is by writing the quotient and the remainder with an "R" in between them. The number 7 divided by 2 can be written as 7/2 = Q=3 and R=1. Here Q=3 is a quotient and R=1 is a remainder.
- Another way to represent the remainder is by showing it as a part of a mixed fraction. The number 7 divided by two can be written as 7/2 = 3½
Properties of Remainder
The properties of the remainder are as follows:
- The remainder is always less than the divisor. A remainder that is either greater than or equal to the divisor indicates that the division is incorrect.
- If one number (divisor) divides the other number (dividend) completely, then the remainder is 0.
- The remainder can be either greater, lesser, or equal to the quotient.
☛Related Articles
Given below is the list of topics that are closely connected to the remainder. These topics will also help you in solving problems related to the remainder.
Remainder Examples
-
Example 1: What is the remainder when 3723 is divided by 23? Check if the answer you got is correct.
Solution:
Let us divide 3723 by 23 using long division.

Therefore, the remainder is 20. Now, we will check the answer by substituting all the values of dividend, divisor, quotient, and the remainder in the following equation: Dividend = Divisor × Quotient + Remainder
3723 = 23 × 161 + 20 = 3703 + 20 = 3723. Since we have the same values on both sides, our answer is correct.
Therefore, the answer to division is correct.
-
Example 2: The number of days in the year 1996 was 366 as it was a leap year. If 1st Jan 1996 was a Monday, what day was it on 1st Jan 1997?
Solution:
It is given that 1st Jan 1996 was a Monday. We know that every day of the week repeats exactly after 7 days. Hence, we will divide 366 by 7

2 is the remainder of the division here. We can say that 1st Jan 1997 = Monday + 2 days = Wednesday.
Therefore, the 1st of January 1997 was a Wednesday.
-
Example 3: A company has a budget of Rs. 10,540 to buy external hard drives. The cost of each hard drive is Rs. 450. (i) How many hard drives can the company buy with the given budget? (ii) How much money will the company be left with after the purchase?
Solution:
The total budget of the company is Rs. 10,540. The cost of each hard drive is Rs. 450. (i) We will divide 10,540 by 450 to find the number of hard drives that the company can buy.

The number of hard drives that the company can buy is nothing but the quotient of the division. Therefore, the number of hard drives bought is 23. (ii) The amount of money that the company is left with is nothing but the remainder of the above division. Therefore, the money left is Rs.190.
-
Example 4: A teacher distributes chocolates to 30 students in her class such that each one gets an equal number. If there are 315 chocolates in total, (i) How many chocolates did each student get? (ii) How many chocolates are left with the teacher after the distribution?
Solution:
The total number of students in the class is 30. The total number of chocolates that the teacher has is 315 (i) We need to divide 315 by 30. The quotient of this division indicates the number of chocolates each student gets, which is 10. (ii) The remainder of this division indicates the number of chocolates that are left with the teacher is 15.

Therefore, each student gets 10 chocolates and 15 are left with the teacher.

FAQs on Remainder
What do you Mean by Remainder?
Remainder, as its name suggests, is something that "remains". In the process of division, the last number left over is the remainder. Dividing a number 17 by 5, we have a remainder of 2. 17 = 5 × 3 + 2. Here the last remaining number 2 is the remainder.
What is an Example of a Remainder?
When 35 toffees are distributed equally among 8 children, each child gets 4 toffees and 3 toffees are left undistributed. Here, 3 is the remainder. You can find more examples of remainders in math. Remainder is the number lesser in value than the divisor or the dividend.
How does a Remainder Work?
The definition of the remainder is the part of a quantity that is left after dividing it into equal groups. For this let us look at a simple example. A number 30 on dividing into 7 parts, we are left with 2. 30 = 7 × 4 + 2. Here the number 2 which is left after the dividing 30, is the remainder.
Is Zero a Remainder?
Yes, 0 can be a remainder when the divisor divides the dividend completely. For example, the remainder when 15 is divided by 3 is 0. This means that the number 15 can be equally divided into 3 parts without any remainder.
What is Quotient and Remainder in Maths?
The quotient is equal to the number of times the divisor divides the dividend. This can be easily understood with a simple example. The number 7 divides 45 into 6 parts and leaves a remainder, 3. Here the number 6 is the quotient. Further 45 = 7 × 6 + 3. Also, here the remaining number 3 is the remainder. The remainder is the number that is left over after the division process.
How to Get Remainder in Maths?
The remainder is obtained after the completion of the division process. It is the last number remaining after the completion of the division process. Dividing the number 50 by 9, the remainder is the number 5.
What is the Remainder Theorem?
Remainder theorem helps us to find the remainder without actually performing the long division process. The polynomial p(x) = 0 if on substitution of the x value, the remaining value is the remainder. It has numerous applications in equations and polynomials. Hence it states that "when a polynomial p(x) is divided by a linear polynomial (x - a), then the remainder is p(a)" (OR) "when a polynomial p(x) is divided by a linear polynomial (ax + b), the remainder is p(-b/a)". Click here to learn more about the remainder theorem formula.
What is the Remainder Formula?
The remainder formula helps in the calculation of the remainder obtained after the division operation between any two values. The division operation in terms of operands can be represented as:
Dividend = Divisor × Quotient + Remainder
visual curriculum