Trigonometry
Trigonometry is the branch of mathematics that deals with the relationship between ratios of the sides of a right-angled triangle with its angles. The ratios used to study this relationship are called trigonometric ratios, namely, sine, cosine, tangent, cotangent, secant, cosecant. The word trigonometry is a 16th century Latin derivative and the concept was given by the Greek mathematician Hipparchus.
Here in the below content, we shall understand the basics of trigonometry, the various identities-formulas of trigonometry, and the real-life examples or applications of trigonometry.
Introduction to Trigonometry
Trigonometry is one of the most important branches in mathematics. The word trigonometry is formed by clubbing words 'Trigonon' and 'Metron' which means triangle and measure respectively. It is the study of the relation between the sides and angles of a right-angled triangle. It thus helps in finding the measure of unknown dimensions of a right-angled triangle using formulas and identities based on this relationship.

Trigonometry Basics
Trigonometry basics deal with the measurement of angles and problems related to angles. There are three basic functions in trigonometry: sine, cosine, and tangent. These three basic ratios or functions can be used to derive other important trigonometric functions: cotangent, secant, and cosecant. All the important concepts covered under trigonometry are based on these functions. Hence, further, we need to learn these functions and their respective formulas at first to understand trigonometry.

In a right-angled triangle, we have the following three sides.
Perpendicular - It is the side opposite to the angle θ.
Base - This is the adjacent side to the angle θ.
Hypotenuse - This is the side opposite to the right angle.
Trigonometric Ratios
There are basic six ratios in trigonometry that help in establishing a relationship between the ratio of sides of a right triangle with the angle. If θ is the angle in a right-angled triangle, formed between the base and hypotenuse, then
- sin θ = Perpendicular/Hypotenuse
- cos θ = Base/Hypotenuse
- tan θ = Perpendicular/Base
The value of the other three functions: cot, sec, and cosec depend on tan, cos, and sin respectively as given below.
- cot θ = 1/tan θ = Base/Perpendicualr
- sec θ = 1/cos θ = Hypotenuse/Base
- cosec θ = 1/sin θ = Hypotenuse/Perpendicular
Trigonometric Table
The trigonometric table is made up of trigonometric ratios that are interrelated to each other – sine, cosine, tangent, cosecant, secant, cotangent. These ratios, in short, are written as sin, cos, tan, cosec, sec, cot, and are taken for standard angle values. You can refer to the trigonometric table chart to know more about these ratios.

Important Trigonometric Angles
Trigonometric angles are the angles in a right-angled triangle using which different trigonometric functions can be represented. Some standard angles used in trigonometry are 0º, 30º, 45º, 60º, 90º. The trigonometric values for these angles can be observed directly in a trigonometric table. Some other important angles in trigonometry are 180º, 270º, and 360º. Trigonometry angle can be expressed in terms of trigonometric ratios as,
- θ = sin-1 (Perpendicular/Hypotenuse)
- θ = cos-1 (Base/Hypotenuse)
- θ = tan-1 (Perpendicular/Base)
List of Trigonometric Formulas
There are different formulas in trigonometry depicting the relationships between trigonometric ratios and the angles for different quadrants. The basic trigonometry formulas list is given below:
1. Trigonometry Ratio Formulas
- sin θ = Opposite Side/Hypotenuse
- cos θ = Adjacent Side/Hypotenuse
- tan θ = Opposite Side/Adjacent Side
- cot θ = 1/tan θ = Adjacent Side/Opposite Side
- sec θ = 1/cos θ = Hypotenuse/Adjacent Side
- cosec θ = 1/sin θ = Hypotenuse/Opposite Side
2. Trigonometry Formulas Involving Pythagorean Identities
- sin²θ + cos²θ = 1
- tan2θ + 1 = sec2θ
- cot2θ + 1 = cosec2θ
3. Sine and Cosine Law in Trigonometry
- a/sinA = b/sinB = c/sinC
- c2 = a2 + b2 – 2ab cos C
- a2 = b2 + c2 – 2bc cos A
- b2 = a2 + c2 – 2ac cos B
Here a, b, c are the lengths of the sides of the triangle and A, B, and C are the angle of the triangle.
The complete list of trigonometric formulas involving trigonometry ratios and trigonometry identities is listed for easy access. Here's a list of all the trigonometric formulas for you to learn and revise.
Trigonometric Functions Graphs
Different properties of a trigonometric function like domain, range, etc can be studied using the trigonometric function graphs. The graphs of basic trigonometric functions- Sine and Cosine are given below:

The domain and range of sin and cosine functions can thus be given as,
- sin θ: Domain (-∞, + ∞); Range [-1, +1]
- cos θ: Domain (-∞ +∞); Range [-1, +1]
Click here to learn about the graphs of all trigonometric functions and their domain and range in detail- Trigonometric Functions
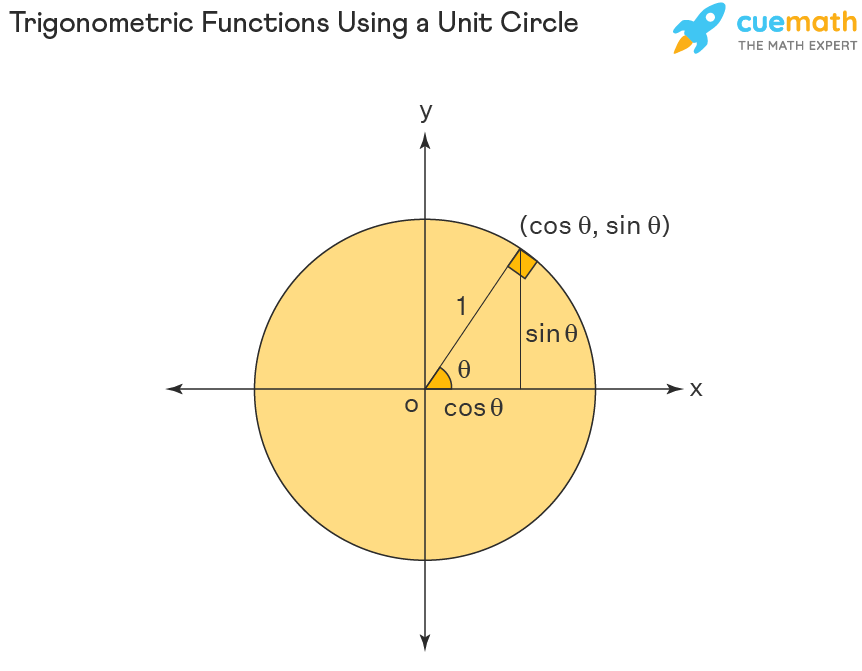
Unit Circle and Trigonometric Values
Unit circle can be used to calculate the values of basic trigonometric functions- sine, cosine, and tangent. The following diagram shows how trigonometric ratios sine and cosine can be represented in a unit circle.
Trigonometry Identities
In Trigonometric Identities, an equation is called an identity when it is true for all values of the variables involved. Similarly, an equation involving trigonometric ratios of an angle is called a trigonometric identity, if it is true for all values of the angles involved. In trigonometric identities, you will get to learn more about the Sum and Difference Identities.
For example, sin θ/cos θ = [Opposite/Hypotenuse] ÷ [Adjacent/Hypotenuse] = Opposite/Adjacent = tan θ
Therefore, tan θ = sin θ/cos θ is a trigonometric identity. The three important trigonometric identities are:
- sin²θ + cos²θ = 1
- tan²θ + 1 = sec²θ
- cot²θ + 1 = cosec²θ
Applications of Trigonometry
Throughout history, trigonometry has been applied in areas such as architecture, celestial mechanics, surveying, etc. Its applications include in:
- Various fields like oceanography, seismology, meteorology, physical sciences, astronomy, acoustics, navigation, electronics, and many more.
- It is also helpful to find the distance of long rivers, measure the height of the mountain, etc.
- Spherical trigonometry has been used for locating solar, lunar, and stellar positions.
Real-Life Examples of Trigonometry
Trigonometry has many real-life examples used broadly. Let’s get a better idea of trigonometry with an example. A boy is standing near a tree. He looks up at the tree and wonders “How tall is the tree?” The height of the tree can be found without actually measuring it. What we have here is a right-angled triangle, i.e., a triangle with one of the angles equal to 90 degrees. Trigonometric formulas can be applied to calculate the height of the tree, if the distance between the tree and boy, and the angle formed when the tree is viewed from the ground is given.

It is determined using the tangent function, such as tan of angle is equal to the ratio of the height of the tree and the distance. Let us say the angle is θ, then
tan θ = Height/Distance between object & tree
Distance = Height/tan θ
Let us assume that distance is 30m and the angle formed is 45 degrees, then
Height = 30/tan 45°
Since, tan 45° = 1
So, Height = 30 m
The height of the tree can be found out by using basic trigonometry formulas.
☛ Related Topics:
- Sine Law
- Cosine Law
- What Is a Radian
- Trigonometric Ratios in Radians
- Tangent Function
- Heights and Distances
Important Notes on Trigonometry
- Trigonometric values are based on the three major trigonometric ratios: Sine, Cosine, and Tangent.
Sine or sin θ = Side opposite to θ / Hypotenuse
Cosine or cos θ = Adjacent side to θ / Hypotenuse
Tangent or tan θ = Side opposite to θ / Adjacent side to θ -
0°, 30°, 45°, 60°, and 90° are called the standard angles in trigonometry.
-
The trigonometry ratios of cosθ, secθ are even functions, since cos(-θ) = cosθ, sec(-θ) = secθ.
Solved Examples on Trigonometry
-
Example 1: The building is at a distance of 150 feet from point A. Can you calculate the height of this building if tan θ = 4/3 using trigonometry?

Solution:
The base and height of the building form a right-angle triangle. Now apply the trigonometric ratio of tanθ to calculate the height of the building.
In Δ ABC, AC = 150 ft, tanθ = (Opposite/Adjacent) = BC/AC
4/3 = (Height/150 ft)
Height = (4×150/3) ft = 200ftAnswer: The height of the building is 200ft.
-
Example 2: A man observed a pole of height 60 ft. According to his measurement, the pole cast a 20 ft long shadow. Find the angle of elevation of the sun from the tip of the shadow using trigonometry.
Solution:
Let x be the angle of elevation of the sun, then
tan x = 60/20 = 3
x = tan-1(3)
or x = 71.56 degreesAnswer: The angle of elevation of the sun is 71.56º.

FAQs on Trigonometry
What is Trigonometry in Math?
Trigonometry is the branch of mathematics that deals with the study of the relationship between the sides of a triangle (right-angled triangle) and its angles. The relationship is presented as the ratio of the sides, which are trigonometric ratios. The six trigonometric ratios are sine, cosine, tangent, cotangent, secant, and cosecant.
What are the Basics of Trigonometry?
Trigonometry basics deal with the measurement of angles and problems related to angles. There are six basic trigonometric ratios: sine, cosine, tangent, cosecant, secant and cotangent. All the important concepts covered under trigonometry are based on these trigonometric ratios or functions.
What are the Applications of Trigonometry?
Trigonometry finds applications in different fields in our day-to-day lives. In astronomy, trigonometry helps in determining the distances of the Earth from the planets and stars. It is used in constructing maps in geography and navigation. It can also be used in finding an island's position in relation to the longitudes and latitudes. Even today, some of the technologically advanced methods which are used in engineering and physical sciences are based on the concepts of trigonometry.
How do You do SOH CAH TOA in Trigonometry?
We use the "SOH CAH TOA" trick to memorize the relationship between trigonometric ratios easily. To remember them, remember the word "SOHCAHTOA"!
- SOH: Sine = Opposite / Hypotenuse
- CAH: Cosine = Adjacent / Hypotenuse
- TOA: Tangent = Opposite / Adjacent
What Does θ Mean in Trigonometry?
θ in trigonometry is used as a variable to represent a measured angle. It is the angle between the horizontal plane and the line of sight from an observer's eye to an object above. θ can be referred to as the angle of elevation or angle of depression, depending upon the object's position, i.e, when the object is above the horizontal line, θ is called the angle of elevation, and for object's position below the horizontal line, it is called the angle of depression.
What are Trigonometry Identities?
Trigonometry identities are equations of trigonometry functions that are always true. Trigonometry identities are often used not only to solve trigonometry problems but also to understand important mathematical principles and solve numerous math problems.
What are the Six Basic Trigonometry Functions?
There are 6 trigonometry functions which are:
- Sine function
- Cosine function
- Tangent function
- Secant function
- Cotangent function
- Cosecant function
What is the Reciprocal of sin in Trigonometry?
The sine function for angle θ in a right-angled triangle in trigonometry is given as, sinθ = perpendicular/hypotenuse. The reciprocal of sin function is given as cosecant function. Therefore, cosecθ = hypotenuse/perpendicular.
How is Trigonometry Used in Real Life?
Trigonometry in real life is used in the naval and aviation industries. It also finds application in cartography (creation of maps). It can be used to design the inclination of the roof and the height of the roof in buildings etc.
Who Invented Trigonometry?
Hipparchus(c. 190–120 BCE), also known as the "father of trigonometry", was the first to construct a table of values for a trigonometric function
visual curriculum