Angle of Depression
The angle of depression is formed when an observer looks down at an object. It is the angle formed between the horizontal line which is straight to the observer's eye and the line of sight. Let us learn more about the angle of depression in this article.
What is Angle of Depression?
The angle of depression is "an angle formed between the horizontal line and the line of sight when an observer looks downwards at an object is known as an angle of depression". It measures the change of angle of our sight when we look down. Suppose you are standing in your kitchen and looking straight, and suddenly you spot an insect crawling on the floor. So, that immediate change in the angle of your sight from straight to downwards is the angle of depression.
Angle of Depression Terminology
The angle of depression involves the following terminology:
- Observer (the person who observes)
- Object (the object that is being observed by the observer)
- Horizontal line (a horizontal ray that starts from the observer)
- Line of sight (the line that connects the observer and the object)
The angle of depression is the angle between the horizontal line and the line of sight. In the following figure, the observer is at 'O' and the object is at 'B'. Let OA be the horizontal line and OB be the line of sight. So, the angle formed between these two, i.e angle AOB is the angle of depression.
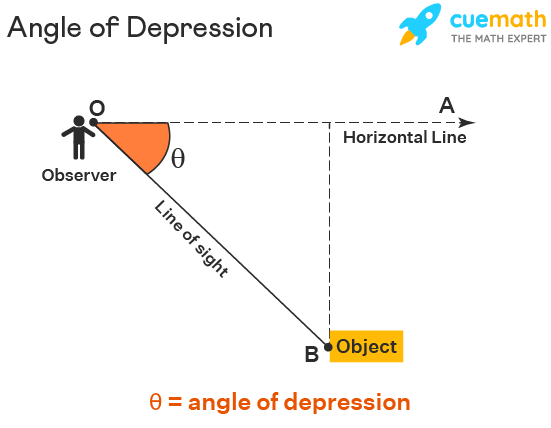
Angle of Depression Formula
The formula for the angle of depression is the same as basic trigonometric ratios formulae. If any two sides of the right triangle formed are known, then we can easily find the required angle by using the angle of depression formulas, that are given below.

Angle of Depression Vs Angle of Elevation
The angle of depression and angle of elevation are opposites of each other. In the angle of depression, the object is placed below the observer, while in the case of the angle of elevation, it is placed above the observer. If you are standing at your terrace and looking at the sun, then the angle of elevation will be formed. On the other hand, if you will look at the dog standing on the road from your terrace, then the angle of depression will be formed. In both cases, we use trigonometry angles to find the heights and distances. Let us understand the difference between the angle of depression and elevation from the image given below.
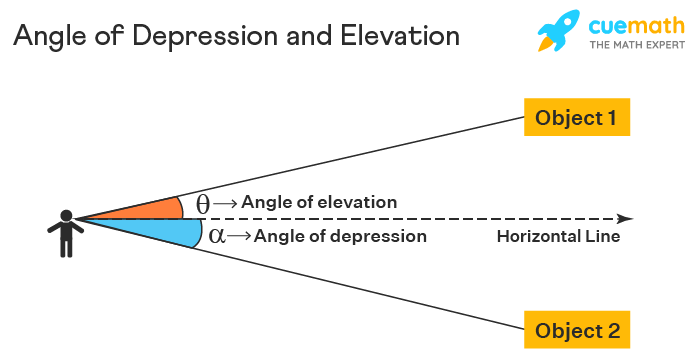
In the above image, θ is the angle of elevation and α is the angle of depression.
Angle of Depression in a Triangle
In a right-angled triangle, the angle of depression is formed at the top of the perpendicular line segment. It is originally at the outside of the triangle, but we use the alternate interior angles theorem to find its alternate angle inside the triangle. For example, in the image given below, if an observer is standing at point A looking down at point C then the angle of depression 'a' is formed with respect to the horizontal axis AD. But, ∠DAC = ∠ACB (by using alternate angles theorem). So, now in the triangle, ABC, the angle of depression is ∠ACB which can be used to find measure the missing side of the triangle.
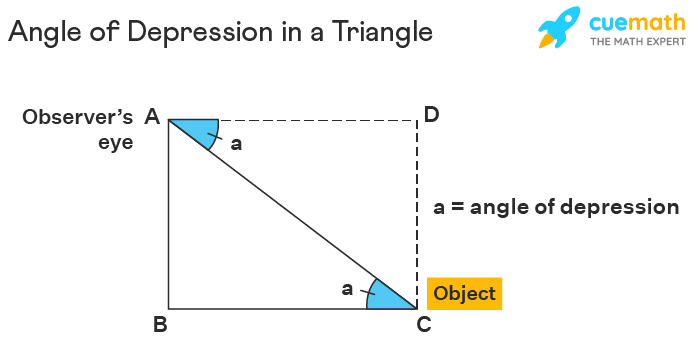
☛ Related Topics:
Check these interesting articles to know more about the concept of the angle of depression and its related topics.
Angle of Depression Examples
-
Example 1: If a person standing at the top of the building of height 50 ft is looking at her daughter standing at a distance of 30 ft away from the building, what will be the angle of depression formed?
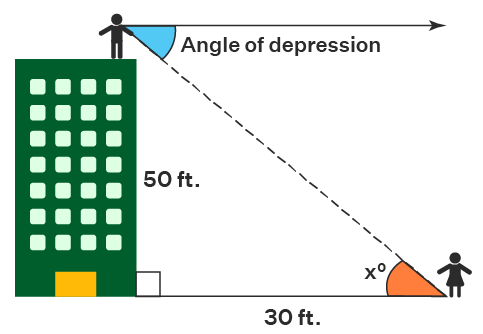
Solution: It is given that the height of the building is 50 ft, and the distance between the building and the girl is 30 ft. Now, in the given figure, the angle of depression is denoted by x° (as the angle of depression and angle x are the same by using alternate interior angles theorem). By using the formula for finding the angle of depression, we get tan x = 50/30.
⇒ tan x = 5/3
⇒ x = tan-1 (5/3)
Answer: Therefore, the angle of depression is tan-1 (5/3).
-
Example 2: Find the value of x in the given figure.
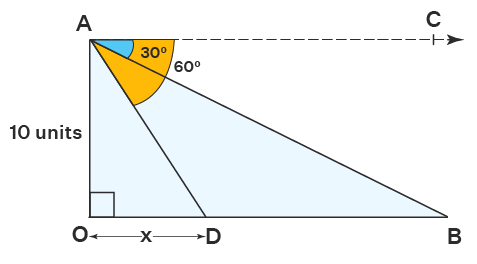
Solution: In the figure given above, there are two angles of depression formed from point A, which are ∠BAC=30° and ∠DAC=60°. We know that, ∠DAC=∠ADO (by using alternate interior angles theorem). So, ∠ADO=60°. By applying the angle of depression formula in △AOD, we get tan 60° = AO/OD.
⇒ √3 = 10/x
⇒ x = 10/√3 units
Answer: Therefore, the value of x is 10/√3 units.
-
Example 3: From a hot air balloon that is flying at a height of 100 ft, the angle of depression of a person on the ground is 30 degrees. Find the length of the rope that is tied from the person on the ground to the balloon.
Solution:
Let the length of the rope be x (in ft).
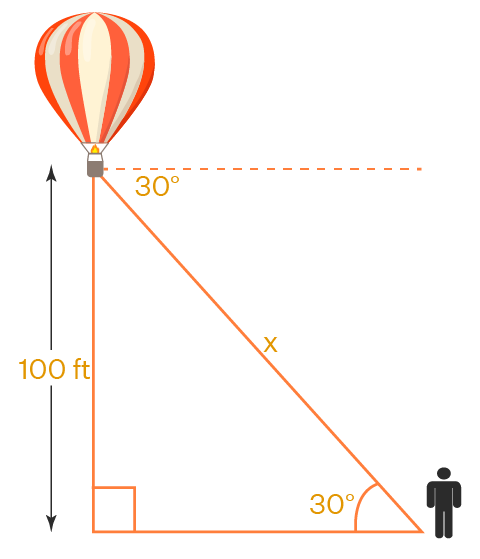
Here, we have written the angle at the person to be 30 degrees by the alternate interior angle theorem.
Now, apply sine for the triangle,
sin 30 = 100/x
x = 100/(sin 30) = 100 / (1/2) = 200 ft
Answer: The length of the rope = 200 ft.

FAQs on Angle of Depression
What is the Definition of Angle of Depression in Trigonometry?
In trigonometry, the angle of depression is the angle formed between the horizontal line and the line of sight when we look downwards at an object. In this angle, the object at which we look is always placed below the horizontal axis or line.
What is the Angle of Elevation and the Angle of Depression?
The angle of elevation and depression are formed on either side of the horizontal line which is the straight line forming an angle of 90 degrees with the object. When we look upwards, the angle of elevation is formed and when we look down at some object, the angle of depression is formed. Both are important in order to find the heights and distances of large structures.
What is the Formula for Angle of Depression?
The formula of the angle of depression is the same as the basic trigonometric ratios formulae, which are given below:
- sin x = perpendicular/hypotenuse
- cos x = base/hypotenuse
- tan x = perpendicular/base
These three formulas can be used to find the angle of depression, based on which two sides of the right triangle are given.
How to Calculate Angle of Depression?
The angle of depression is the angle formed between the horizontal line and the line of sight which is below the horizontal line. It always forms a right-angled triangle between the observer, line, and the object. To calculate the angle of depression, we can use any of the basic trigonometric formulas of sine, cosine, and tangent, depending on which two sides of the triangle are given.
How to Find Distance with Angle of Depression?
To find distance with the angle of depression, we can use trigonometric formulas for calculations. Suppose, a girl is standing at the top of a 10 meters long tower making an angle of depression of 45 degrees with a bicycle standing on the road. Then the distance between the bicycle and the tower can be found by using the tangent formula which is tan 45° = 10/distance. Now, tan 45°=1, so, 1 = 10/distance, which means distance is equal to 10 units.
Is Angle of Depression and Inclination the Same?
The angle of inclination is the angle that forms above the horizontal axis. It is the same as the angle of elevation. The angle of depression is the same as the angle of declination as both are formed below the horizontal axis with a downward slope.
How is Angle of Depression Related to Real Life?
The angle of depression is used to measure heights and distances involving large calculations. It is used in architecture, engineering, science, etc.
How Do You Find Angle of Elevation and Depression?
Angle of elevation is the angle between a horizontal line of sight and the object when a person is looking up at an object. Whereas the angle of depression is the angle between the horizontal line of sight and the object when a person is looking down at an object.
What is the Importance of Angle of Elevation and Depression?
One of the main aspects of using the angle of elevation and depression is that it is used mostly in word problems in trigonometry when there are is a line of sight involved. These angles are used in solving trigonometric problems such as sine, cosine, and tangent along with inverse trigonometric functions.
visual curriculum