Triangle
A triangle is a closed shape with 3 angles, 3 sides, and 3 vertices. A triangle with three vertices P, Q, and R is represented as △PQR. The most commonly seen examples of triangles are the signboards and sandwiches that are in the shape of a triangle. Let us read more about the triangle shape, the definition of a triangle, the parts of a triangle, the kinds of triangles and the properties of triangles on this page.
| 1. | What is a Triangle? |
| 2. | Properties of Triangles |
| 3. | Triangle Formulas |
| 4. | Classification of Triangles |
| 5. | FAQs on Triangle |
What is a Triangle?
A triangle is a simple polygon with 3 sides and 3 interior angles. It is one of the basic shapes in geometry in which the 3 vertices are joined with each other and it is denoted by the symbol △. There are various types of triangles that are classified on the basis of the sides and angles.
Parts of a Triangle
A triangle consists of various parts. It has 3 angles, 3 sides, and 3 vertices. Observe the triangle PQR given below which shows the sides, the vertices and the interior angles of a triangle.

In the triangle given above:
- The three angles are, ∠PQR, ∠QRP, and ∠RPQ.
- The three sides are side PQ, side QR, and side RP.
- The three vertices are P, Q, and R
Note: The sum of all the angles of the triangle is equal to 180°.
Properties of Triangles
All geometrical shapes have different properties related to sides and angles that help us to identify them. The important properties of a triangle are listed below.
- A triangle has three sides, three vertices, and three interior angles.
- The angle sum property of a triangle states that the sum of the three interior angles of a triangle is always 180°. Observe the triangle PQR given above in which angle P + angle Q + angle R = 180°.
- The Triangle inequality theorem states that the sum of the length of the two sides of a triangle is greater than the third side.
- As per the Pythagoras theorem, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides i.e., (Hypotenuse² = Base² + Altitude²)
- The side opposite the greater angle is the longest side.
- The Exterior angle theorem of a triangle states that the exterior angle of a triangle is always equal to the sum of the interior opposite angles.
Triangle Formulas
In geometry, for every two-dimensional shape (2D shape), there are always two basic measurements that we need to find out, i.e., the area and perimeter of that shape. Therefore, the triangle has two basic formulas which help us to determine its area and perimeter. Let us discuss the formulas in detail.
Perimeter of Triangle
The perimeter of a triangle is the sum of all three sides of the triangle. Observe the triangle given below which shows that the perimeter of the triangle is the sum of all its sides.

Perimeter of Triangle formula = a + b + c
Area of a Triangle
The area of a triangle is the space covered by the triangle. It is half the product of its base and altitude (height). It is always measured in square units, as it is two-dimensional. Observe the triangle ABC given below which shows the base and height of a triangle which are used to calculate the area of a triangle.

Area of ΔABC = 1/2 × BC × AD
Here, BC is the base and AD is the height of the triangle.
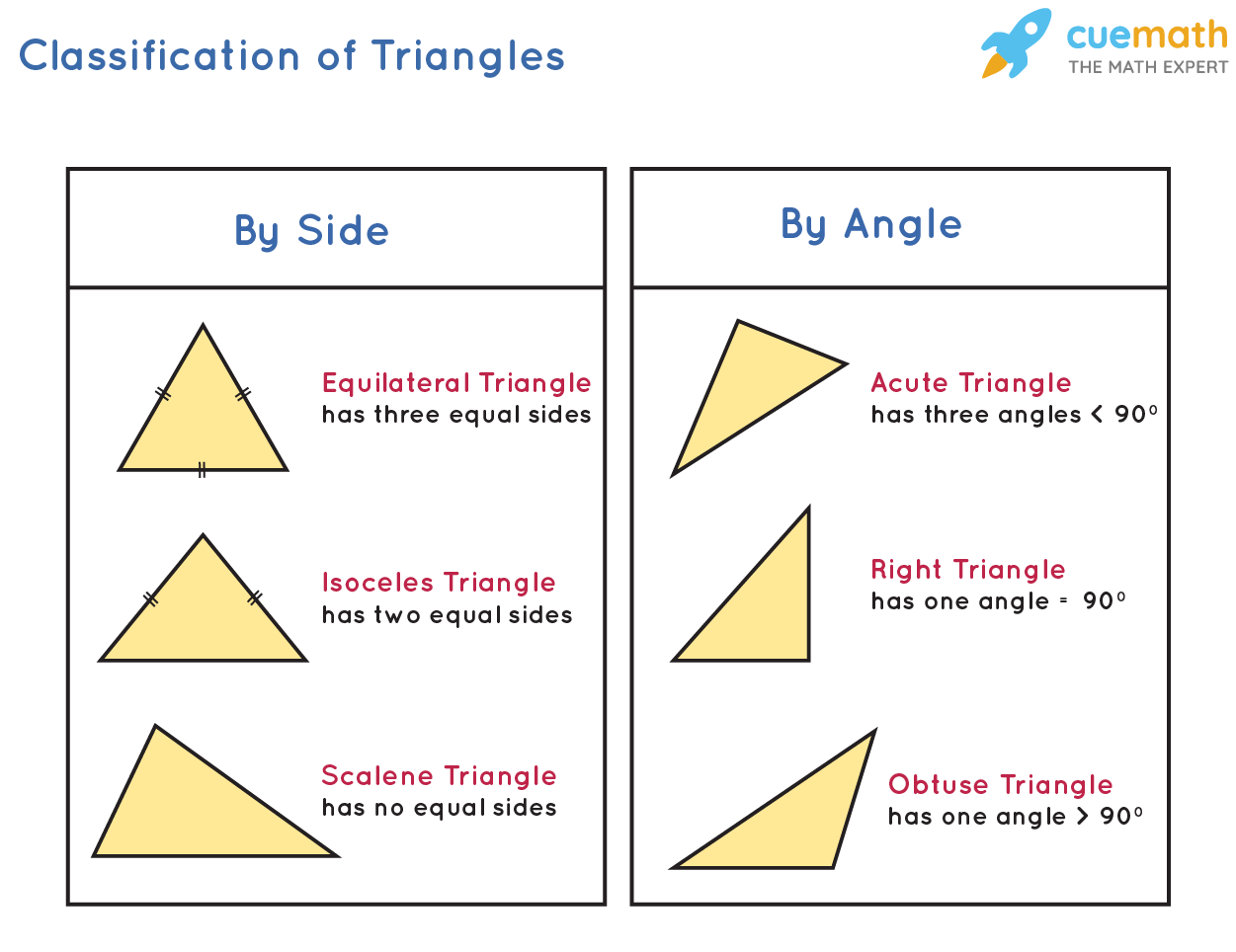
Classification of Triangle
Triangles can be classified on the basis of their sides and angles. Let us understand the classification of triangles with the help of the table given below which shows the difference between 6 different types of triangles on the basis of angles and sides.
Kinds of Triangles
The following figure shows the different kinds of triangles categorized on the basis of sides and angles.
Important Notes on Triangle
- A triangle is a 3-sided closed shape.
- There are two important formulas related to triangles, i.e., the Heron's formula and Pythagoras theorem.
- The sum of the interior angles of a triangle is 180° and is expressed as ∠1 + ∠2 + ∠3 = 180°.
☛Related Articles
Check out these interesting articles to know more about triangles and topics related to triangles.
Triangle Examples
-
Example 1: The perimeter of a triangle is given as 26 feet. If two of its sides measure 7 feet and 11 feet respectively, what is the measure of the third side?
Solution:
We know that the perimeter of a triangle is the sum of all three sides. Since we know the length of 2 sides, the length of the 3rd side can be calculated using the formula,
Perimeter = side 1 + side 2 + side 3. After substituting the given values, we get,
⇒ 26 = 7 + 11 + unknown side
Therefore, the unknown side is
=26 - (7 +11) = 8 feet
∴ The third side of the given triangle measures 8 feet.
-
Example 2: Emma is building a triangular wooden birdhouse. If two of the angles measure 45° and 63°, what is the measure of the third angle?
Solution:
We know that the sum of the angles of a triangle adds up to 180°. Therefore, the unknown angle can be calculated using the formula
Sum of interior angles of a triangle = Angle 1 + Angle 2 + Angle 3
⇒ 180° = 45° + 63° + Angle 3
⇒ Angle 3 = 180° - (45° + 63°)
Angle 3 ⇒ 72°
∴ The third angle is 72°.
-
Example 3: The height of a triangle is 360 feet and the base is 270 feet. Find the area of the triangle.
Solution:
The height of the triangle = 360 feet and base = 270 feet
The area of a triangle is = 1/2 × Base × Height
Area of the triangle = 1/2 × 270 × 360 = 48600 feet2
∴ Area of the triangle = 48,600 feet2

FAQs on Triangle
What is a Triangle in Maths?
In geometry, a triangle is defined as a two-dimensional shape with three sides, three interior angles, and three vertices. It is a simple polygon in which the 3 vertices are joined with each other and it is denoted by the symbol △.
What are the Two Basic Triangle Formulas?
The two basic triangle formulas are the area of a triangle and the perimeter of a triangle. These triangle formulas can be mathematically expressed as;
- Area of triangle, A = [(½) b × h]; where 'b' is the base of the triangle and 'h' is the height of the triangle.
- Perimeter of a triangle, P = (a + b + c); where 'a', 'b', and 'c' are the 3 sides of the triangle.
How many Types of Triangles are there in Maths?
There are six types of triangles categorized on the basis of sides and angles as listed below:
- Scalene triangle
- Isosceles triangle
- Equilateral triangle
- Acute triangle
- Obtuse triangle
- Right-angled triangle
Are Isosceles Triangles Always Acute?
No, an isosceles triangle can be an acute angle, right angle, or obtuse-angled triangle depending upon the measure of the angles it has.
What is the Area of a Scalene Triangle?
The area of a scalene triangle is half of the product of the base and the height of the triangle. Thus, the area of the scalene triangle, with a base 'b and height 'h' is expressed as Area of scalene triangle = 1/2 × b × h
What is the Formula Used for Finding the Area of a Right Triangle?
The formula used for finding the area of a right triangle of base (b) and height (h) is, Area of a right triangle = 1/2 × base × height.
What is an Equilateral Triangle?
An equilateral triangle is a regular polygon in which all the 3 sides are of equal length and the interior angles are of equal measure. This means each interior angle of an equilateral triangle is equal to 60°.
What is an Isosceles Triangle?
In a triangle, if the length of only two sides is equal and the measure of corresponding opposite angles is also equal, then the triangle is said to be an isosceles triangle.
What is a Right Triangle in Geometry?
A right triangle is a triangle in which one angle is equal to 90° (right angle). In geometry we have three different names for all the three sides of a right-angled triangle:
- The hypotenuse (the longest side or the side opposite to the 90° angle)
- The base
- The perpendicular (altitude).
What is the Area and Perimeter of a Triangle?
The area of a triangle is the total space occupied within the boundary of a particular triangle. The perimeter of a triangle is the total length of the boundary of the triangle.
visual curriculum