Perimeter
Perimeter is the total length of the boundary of any closed shape. Let’s try and understand this using an example. For example, you have a huge square-shaped farm. Now, in order to save your farm from street animals, you decide to fence it. If you know the length of one side of the farm, you just have to multiply it by 4 in order to find the total length of the boundary of the farm. There are many such instances where we might be using the concept of finding perimeter without even knowing about it.
| 1. | What is Perimeter? |
| 2. | How to Find Perimeter? |
| 3. | Perimeter Formula |
| 4. | Difference Between Perimeter and Area |
| 5. | FAQs on Perimeter |
What is Perimeter?
The perimeter of a shape is defined as the total distance around the shape. It is the length of the outline or boundary of any two-dimensional geometric shape. The perimeter of different figures can be equal in measure depending upon the dimensions. For example, imagine a triangle made of a wire of length L. The same wire can be reused to make a square, considering that all the sides are equal in length. Look at the image below showing the perimeter of a rectangular park.
How to Find Perimeter?
The outer boundary that makes up a geometrical shape is called its perimeter. Now, how does one calculate the perimeter? Let us consider an example. David wants to put a fence around his farm so that his sheep will not wander away. He wants to know how much wire he would need to fence around his farm. The shape of his farm is rectangular, which means that:
- It has four sides.
- The opposite sides are of equal length.
- All angles are 90 degrees each.
Let us first name the sides of his farm. The larger side of this rectangular farm is named l, and the smaller side is named b. Now, if we add the distance of all 4 sides of his farm, it will give us the perimeter. Total distance = l + b + l + b = 2l + 2b. Therefore, the perimeter of a rectangle = 2 (l+b) units.
Perimeter Units
Perimeter is the measure of length covered by the boundary of the shape. So, the units of the perimeter will be the same as the units of length. We can say that perimeter is one-dimensional. Hence, it can be measured in meters, kilometers, centimeters, and so on. Some other units of measuring perimeter that are accepted worldwide are inches, feet, yards, and miles.
Perimeter Formula
The total length of the boundary of a closed shape is called its perimeter. Imagine a square-shaped chocolate piece with a side length of 1 inch. The perimeter of any 2-dimensional figure is measured as the sum of all the sides. Hence, the perimeter of a given square-shaped chocolate piece is 1+1+1+1 = 4 inches. Its formula is Perimeter = Sum of all the sides. The perimeter formulas for different 2-D figures are shown in the table below:
|
Shape |
Perimeter Formulas |
|---|---|
| Square | Perimeter of a square = 4 × L where L = length of a side. |
| Perimeter of a rectangle = 2 × (l + b) where l,b = length, and breadth of the rectangle respectively |
|
| Perimeter of a triangle = a + b + c where a, b, c = lengths of 3 sides |
|
| Perimeter of a quadrilateral = a + b + c + d where a, b, c, d = lengths of 4 sides |
|
| Perimeter of a circle = 2πr where r = radius, and π = 22/7 or 3.14 approx |
Difference Between Perimeter and Area
The area is the space occupied or enclosed by a closed shape whereas the perimeter is the total distance covered around the edge of the shape. We define the area as the amount of space covered by a flat surface of a particular shape. It is measured in terms of the "number of" square units (square yards, square inches, square feet, etc.). Most objects or shapes have edges and corners. The length and breadth of these edges are considered while calculating the area of a specific shape. On the other hand, the perimeter is the measure of length covered by the boundary of the shape. First, have a look at the image given here to understand the area vs perimeter of a rectangle.
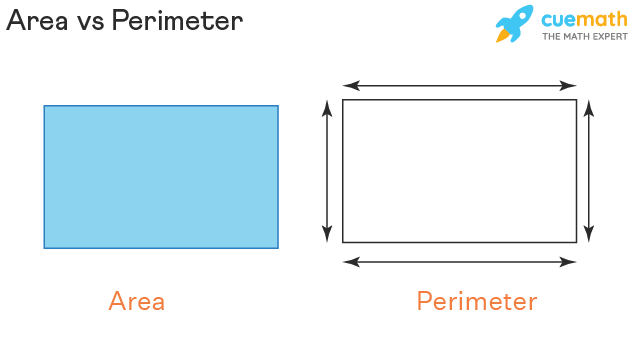
When the area is the space enclosed inside the boundary, the perimeter is the length of that boundary. The area is always measured in square units as it is two-dimensional, and the perimeter is always measured in units as it is one-dimensional. We know that the perimeter of a rectangle is 2(l + b) units; while the area of a rectangle is l × b square units. Similarly, the area of a square is a2, while the perimeter of a square is 4a. Let us have a look at the formulas for the area and perimeter of some of the common shapes:
| Area of square = side2 | Perimeter of square = 4 × side |
| Area of a rectangle = length × breadth | Perimeter of rectangle = 2(length+breadth) |
| Area of triangle = ½ × base × height | Perimeter of triangle = Sum of all three sides |
| Area of rhombus = ½ (product of diagonals) | Perimeter of rhombus = 4 × side |
| Area of trapezium = ½ × (sum of parallel sides) × height | Perimeter of trapezium = sum of all 4 sides |
☛ Related Articles
Check these interesting articles related to the concept of the perimeter in math.
Perimeter Examples
-
Example 1: Your favorite chocolate bar is made up of 6 unit squares with each side of the square measuring 1 in. Calculate its perimeter.
Solution:
We know that each little square has all its sides = 1 in each. If we count and add the sides of squares along the length of the bar, we get 3 inches. The sides of squares along the breadth of the bar add up to 2 inches. Therefore, the length of the bar = 3 in, and the breadth of the bar = 2 in. ∴ The perimeter of the chocolate bar is 2(3 + 2) = 2 × 5 = 10 inches.
FAQs on Perimeter
What is a Perimeter in Math?
The total length of the boundary of any closed 2-dimensional shape is called its perimeter. In the case of a circle, we can also call it circumference.
What is a Perimeter of a Shape?
The total length of the outer boundary of a closed shape is called its perimeter. It is calculated by adding the lengths of all the sides.
What is the Perimeter of a Square?
The perimeter of a square is the sum of all its four sides. As we know that all four sides of a square are equal in measure, therefore its perimeter can be calculated as 4 × side-length. Consider a square of side 4 meters. So, perimeter = 4 × 4 = 16 m.
What is the Perimeter of a Rectangle?
Perimeter of a rectangle is the sum of all four sides of a rectangle. As the opposite sides of a rectangle are equal in measurement, its perimeter is length + length + breadth + breadth or 2 (length + breadth). Consider a rectangular table with length 30 in and breadth 25 in. Therefore, the perimeter of the table = 2 (l+b) = 2 (30+25) = 2 (55) = 110 inches.
What is the Perimeter of a Triangle?
The perimeter of a triangle is the sum of all three sides. In the case of an equilateral triangle, since all three sides are equal in length, the perimeter can be calculated as 3 × side-length. The formula of perimeter of triangle = (a + b + c) units, where a, b, and c are the sides of the triangle.
Where do we Use Perimeter in Real Life?
Perimeter is very useful in real life and plays a crucial role. If you are planning to construct a house then an accurate perimeter is required of doors, windows, roof, walls, etc. If you want to decorate any item with a ribbon, then also we need to estimate the perimeter to buy the approximate length of the ribbon.
What is the Formula for Perimeter?
The total length of the boundary of a closed shape is called its perimeter. Hence, the perimeter of that shape is measured as the sum of all the sides. Thus, the perimeter formula is Perimeter(P) = Sum of all the sides.
What is the Perimeter of Polygon Definition?
The perimeter of a polygon is the measurement of the total length of the boundary in a two-dimensional plane. It is expressed in terms of cm, m, ft, inches, etc.
What is the Perimeter of Parallelogram?
The perimeter of a parallelogram is the sum of all its sides. The opposite sides of a parallelogram are equal. Thus, the formula used to determine the perimeter of a parallelogram of sides 'a' and 'b' is a + a + b + b (or) 2a + 2b units.
What is the Perimeter of a Rhombus?
The perimeter of a rhombus is the sum of all its sides. Since all the four sides of a rhombus are equal, the formula used to calculate the perimeter of a rhombus is:
Perimeter of rhombus formula = a + a + a + a = 4a, where 'a' represents the side length of the rhombus.
What is Perimeter of a Kite Formula?
The sum of all the sides of the kite is called the perimeter of the kite. This length may be calculated by adding the sides of each pair.
What is the Perimeter of Circle When Diameter is Given?
If the diameter is given, the perimeter of the circle formula = πd. Where d is diameter and π is a constant with value (3.14 or 22/7). In terms of radius, the perimeter of the circle formula = 2 π r, where r is radius and value of D = 2r.
What is the Perimeter of Semicircle Formula?
The perimeter of the semicircle is the sum of the length of the diameter and half the circumference of the original circle. It is mathematically expressed as:
Perimeter = (πr + 2r), where "r" is the radius of the semicircle and π is a constant with a value of 22/7.
In terms of diameter, the formula is expressed as, Perimeter = π(d/2) + d, where 'd' is the diameter of the semicircle.
What is the Difference Between Area and Perimeter?
The area is the space occupied by a shape whereas the perimeter is the total distance covered around the edge of the shape. The area is two-dimensional, while the perimeter is one-dimensional as it is the total length of the boundary of a shape.