Perimeter of Right Angled Triangle
The perimeter of a geometrical shape is the total length of its boundary. Hence, the perimeter of a right-angled triangle means the total sum of all its sides. Let us explore the various formulas and techniques related to the perimeter of a right-angled triangle.
| 1. | What is the Perimeter of a Right Triangle? |
| 2. | How to Find the Perimeter of a Right Triangle? |
| 3. | FAQs on Perimeter of a Right Triangle |
What is the Perimeter of a Right Angled Triangle?
The perimeter of a right triangle is the sum of all its sides. For example, if a, b, and c are the sides of a right-angled triangle, then its perimeter will be: (a + b + c). Now, since it is a right triangle, it can be said that its perimeter is the sum of the lengths of the two sides and the hypotenuse. Observe the following figure which shows a right-angled triangle with sides a, b, and c, where c is the hypotenuse and a, b are the sides that together form a 90° angle. The three sides can be named as follows: a = height, b = base, and c = hypotenuse.
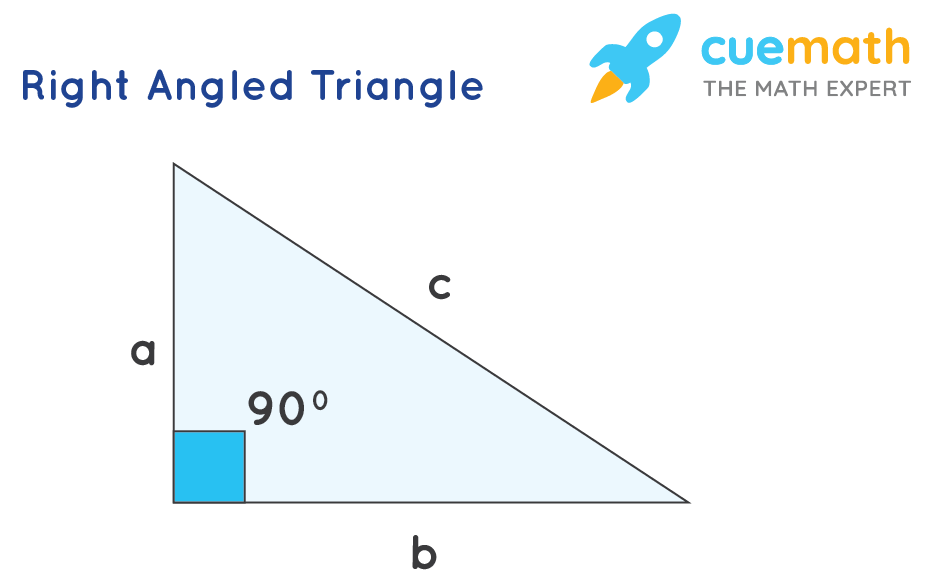
How to Find the Perimeter of a Right Triangle?
There are various methods to find the perimeter of a right triangle. For this, we need to check the parameters according to the given condition. Let us see the various methods as per the given parameters.
Methods to Find the Perimeter of Right Angled Triangle
Method 1: When all the sides of the right-angled triangle are given.
If we know the length of all the sides of the right-angled triangle, then we just need to sum up their lengths. For example, if p, q, and r are the given sides, then the perimeter = p + q + r. This method is only possible when the measurements of all the sides are known.
Method 2: When the side lengths are not given but the right-angled triangle is drawn to scale.
In this case, we use a ruler to measure the sides and add the measurements of each side. The perimeter of the right-angled triangle = sum of all the sides measured by the ruler.
Method 3: When any two sides of a right-angled triangle are given.
In this case, we first find the missing side using the Pythagoras theorem, and then we calculate the perimeter of the right triangle. The Pythagoras theorem states that the square of the length of the hypotenuse is equal to the sum of the squares of the other two sides of a right-angled triangle. (Hypotenuse)2 = (Base)2 + (Height)2
Observe the triangle given below, where 'a' and 'b' are the sides that together form the 90° angle, and 'c' is the hypotenuse. For this, the Pythagoras theorem is written as: c2 = a2 + b2
Now, using this Pythagoras theorem: c2 = a2 + b2, the following formulas can be derived to find the missing side.
- a =\(\sqrt{c^2 - b^2}\)
- b =\(\sqrt{c^2 - a^2}\)
- c =\(\sqrt{a^2 + b^2}\)
After the missing side is found, the perimeter of the right-angled triangle can be calculated with the same basic formula: P = a + b + c
Note: The following formulas can also be used directly when one of the sides are not known:
Perimeter = a + b + \(\sqrt{a^2 + b^2}\) (when c is not given)
Perimeter = b + c + \(\sqrt{c^2 - b^2}\) (when a is not given)
Perimeter = c + a + \(\sqrt{c^2 - a^2}\) (when b is not given)
Related Articles on Perimeter of Right Triangle
Check out the following articles to learn more about the perimeter of right-angled triangle.
FAQs on Perimeter of a Right Triangle
What is the Perimeter of a Right Angled Triangle in Math?
The perimeter of a right-angled triangle is the sum of the length of all three sides, which includes the hypotenuse, the height (altitude), and the base. If x, y, and z are the sides of a right-angled triangle, then its perimeter = (x + y + z).
What is the Pythagoras Theorem for a Right Angled Triangle?
The Pythagoras theorem states that in a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the other two sides. For example, if 'a' and 'b' are the sides that form the 90° angle and 'c' is the hypotenuse then the Pythagoras theorem is written as c2 = a2 + b2.
What is the Difference Between Area and Perimeter of a Right Angled Triangle?
The area of a right-angled triangle is the amount of space that it occupies. It is calculated with the help of the formula: Area = ½ × base × height. The perimeter of a right-angled triangle is the total length of its boundary or the sum of the lengths of all three sides, which includes the hypotenuse, the height, and the base. This is calculated with the formula: P = base + height + hypotenuse.
What is the Formula of Perimeter of Right Angled Triangle?
The formula of the perimeter of a right-angled triangle is the sum of all sides. Suppose p, q, r are the sides of the triangle then perimeter = p + q + r.
How to Find the Area and Perimeter of a Triangle?
To find the area of a triangle, we use the formula: Area = ½ × base × height and the answer is expressed in square units. The perimeter of a triangle with sides x, y, and z can be calculated using the formula: Perimeter = x + y + z and the answer is expressed in units.
What is the Greatest Possible Perimeter of a Right Triangle if One of the Sides has a Length 12?
The greatest possible perimeter of a right triangle is 84 (12 + 35 + 37) and the sides of the triangle are 12, 35, 37. Suppose b is the breadth and a is hypotenuse and length is 12 (given). Using Pythagoras theorem, b2 + (12)2 = a2
(a2 - b2) = 144 ⇒ (a + b)(a -b) = 144. Making the list of all possible ways of expressing 144 as the product of two numbers both of which are even. The answer comes from the fact that 144 = 2 × 72. Now by decomposition, we get a = 35 and b = 37.