Area of Triangle
The area of a triangle is defined as the total space occupied by the three sides of a triangle in a 2-dimensional plane. The basic formula for the area of a triangle is equal to half the product of its base and height, i.e., A = 1/2 × b × h. This formula is applicable to all types of triangles, whether it is a scalene triangle, an isosceles triangle, or an equilateral triangle. It should be remembered that the base and the height of a triangle are perpendicular to each other.
In this lesson, we will learn the area of triangle formulas for different types of triangles, along with some examples.
What is the Area of a Triangle?
The area of a triangle is the region enclosed within the sides of the triangle. The area of a triangle varies from one triangle to another depending on the length of the sides and the internal angles. The area of a triangle is expressed in square units, like, m2, cm2, in2, and so on.
Triangle Definition
A triangle is a closed figure with 3 angles, 3 sides, and 3 vertices. It is one of the most basic shapes in geometry and is denoted by the symbol △. There are different types of triangles in math that are classified on the basis of their sides and angles.
Area of Triangle Formula
The area of a triangle can be calculated using various formulas. For example, Heron’s formula is used to calculate the triangle’s area, when we know the length of all three sides. Trigonometric functions are also used to find the area of a triangle when we know two sides and the angle formed between them. However, the basic formula that is used to find the area of a triangle is:
Area of triangle = 1/2 × base × height
Observe the following figure to see the base and height of a triangle.
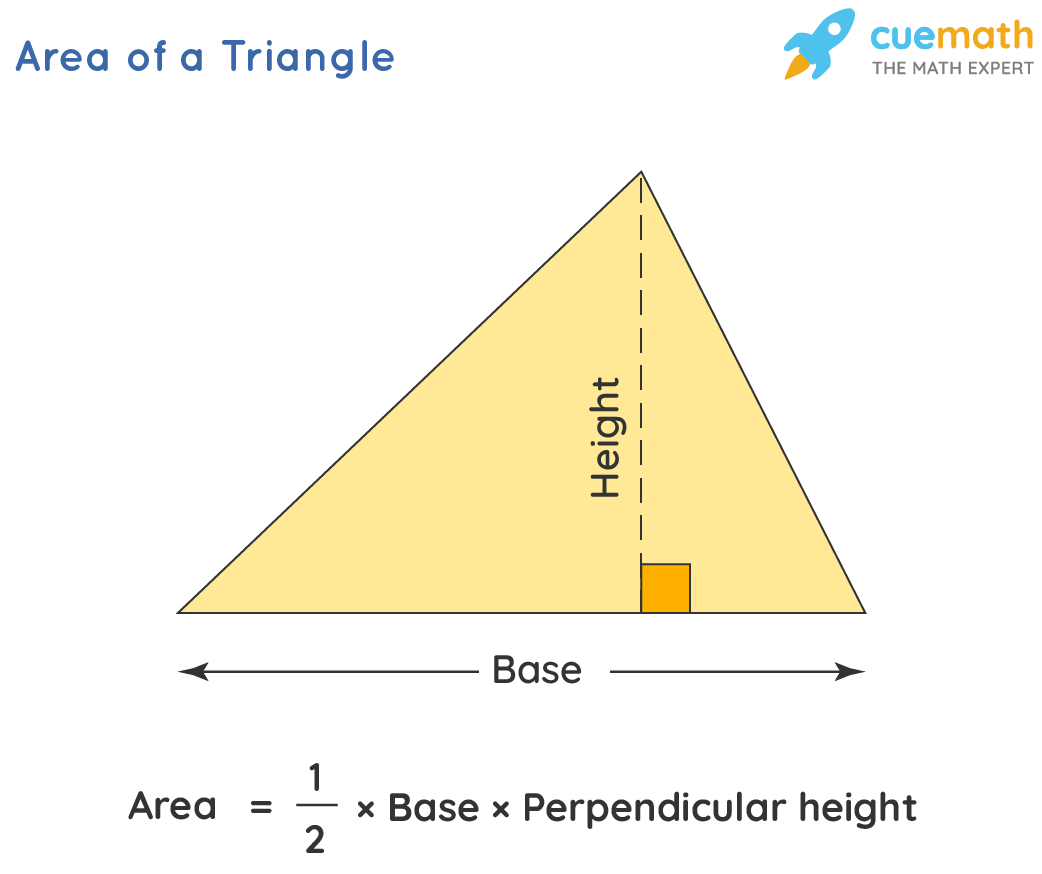
Let us find the area of a triangle using this formula.
Example: What is the area of a triangle with base 'b' = 2 cm and height 'h' = 4 cm?
Solution: Using the formula: Area of a Triangle, A = 1/2 × b × h = 1/2 × 4 × 2 = 4 cm2
Triangles can be classified based on their angles as acute, obtuse, or right triangles. They can be scalene, isosceles, or equilateral triangles when classified based on their sides. Let us learn about the other ways that are used to find the area of triangles with different scenarios and parameters.
Area of Triangle Using Heron's Formula
Heron's formula is used to find the area of a triangle when the length of the 3 sides of the triangle is known. To use this formula, we need to know the perimeter of the triangle which is the distance covered around the triangle and is calculated by adding the length of all three sides. Heron’s formula has two important steps.
- Step 1: Find the semi perimeter (half perimeter) of the given triangle by adding all three sides and dividing it by 2.
- Step 2: Apply the value of the semi-perimeter of the triangle in the main formula called 'Heron’s Formula'.
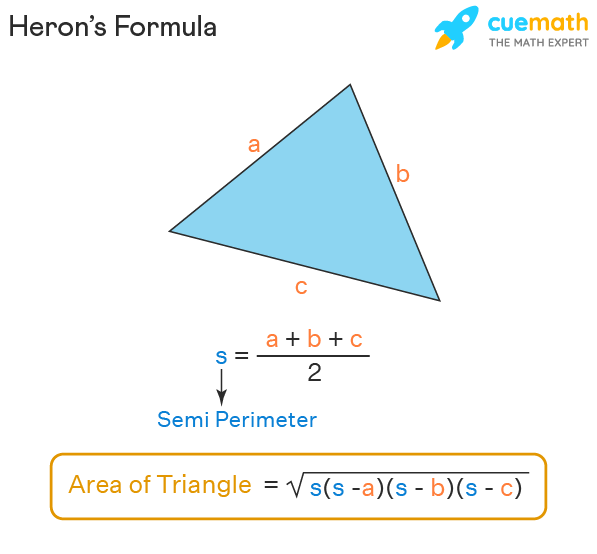
Consider the triangle ABC with side lengths a, b, and c. To find the area of the triangle we use Heron's formula:
Area = \(\sqrt {s(s - a)(s - b)(s - c)}\)
Note that (a + b + c) is the perimeter of the triangle. Therefore, 's' is the semi-perimeter which is: (a + b + c)/2
Area of Triangle With 2 Sides and Included Angle (SAS)
When two sides and the included angle of a triangle are given, we use a formula that has three variations according to the given dimensions. For example, consider the triangle given below.
When sides 'b' and 'c' and included angle A is known, the area of the triangle is:
Area (∆ABC) = 1/2 × bc × sin(A)
When sides 'a' and 'b' and included angle C is known, the area of the triangle is:
Area (∆ABC) = 1/2 × ab × sin(C)
When sides 'a' and 'c' and included angle B is known, the area of the triangle is:
Area (∆ABC) = 1/2 × ac × sin(B)
Example: In ∆ABC, angle A = 30°, side 'b' = 4 units, side 'c' = 6 units.
Area (∆ABC) = 1/2 × bc × sin A
= 1/2 × 4 × 6 × sin 30º
= 12 × 1/2 (since sin 30º = 1/2)
Area = 6 square units.
How to Find the Area of a Triangle?
The area of a triangle can be calculated using various formulas depending upon the type of triangle and the given dimensions.
Area of Triangle Formulas
The area of triangle formulas for all the different types of triangles like the equilateral triangle, right-angled triangle, and isosceles triangle are given below.
Area of a Right-Angled Triangle
A right-angled triangle, also called a right triangle, has one angle equal to 90° and the other two acute angles sum up to 90°. Therefore, the height of the triangle is the length of the perpendicular side. The formula that is used in this case is:
Area of a Right Triangle = A = 1/2 × Base × Height
Area of an Equilateral Triangle
An equilateral triangle is a triangle where all the sides are equal. The perpendicular drawn from the vertex of the triangle to the base divides the base into two equal parts. To calculate the area of the equilateral triangle, we need to know the measurement of its sides. The formula that is used in this case is:
Area of an Equilateral Triangle = A = (√3)/4 × side2
Area of an Isosceles Triangle
An isosceles triangle has two of its sides equal and the angles opposite the equal sides are also equal. The formula that is used in this case is:
Area of an Isosceles Triangle = A = \(\frac{1}{4}b\sqrt {4{a^2} - {b^2}}\)
where 'b' is the base and 'a' is the measure of one of the equal sides.
Area of Triangle when 3 Sides are Given
The area of a triangle can be calculated when 3 sides are given. In this scenario, we assume that all the 3 sides of the triangle are of different lengths. In other words, this is a scalene triangle and we use the Heron's formula to find the area of the triangle. The Heron's formula is explained above on this page and is expressed as follows: Area of triangle = \(\sqrt {s(s - a)(s - b)(s - c)}\) where a, b, and c are the sides of the triangle and 's' is the semi-perimeter; s = (a + b + c)/2.
Observe the table given below which summarizes all the formulas for the area of a triangle.
| Given Dimensions | Area of Triangle Formula |
|---|---|
| When the base and height of a triangle are given. | A = 1/2 (base × height) |
| When the sides of a triangle are given as a, b, and c. |
(Heron's formula) Area of a scalene triangle = \(\sqrt {s(s - a)(s - b)(s - c)}\) |
| When two sides and the included angle is given. | A = 1/2 × side 1 × side 2 × sin(θ) where θ is the angle between the given two sides |
| When base and height is given. | Area of a right-angled triangle = 1/2 × Base × Height |
| When it is an equilateral triangle and one side is given. | Area of an equilateral triangle = (√3)/4 × side2 |
| When it is an isosceles triangle and an equal side and base is given. | Area of an isosceles triangle = 1/4 × b\(\sqrt {4{a^2} - {b^2}}\) where 'b' is the base and 'a' is the length of an equal side. |
- Area of Rectangle
- Area of square
- Area of Circle
- Perimeter of Triangle
- Difference Between Area and Perimeter
Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12. Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.
FAQs on Area Of Triangle
What is the Area of a Triangle?
The area of a triangle is the space enclosed within the three sides of a triangle. It is calculated with the help of various formulas depending on the type of triangle and is expressed in square units like, cm2, inches2, and so on.
What is the Area of Triangle Formula?
The basic formula to find the area of a triangle is, area of triangle = 1/2 (b × h); where 'b' is the base and 'h' is the height of the triangle. However, there are other formulas that are used to find the area of a triangle which depend upon the type of triangle and the known dimensions.
How to Find the Area of a Triangle?
The area of a triangle can be calculated if the base and height of the triangle is given. The basic formula that is used to calculate the area is, Area of triangle = 1/2 (base × height). In other scenarios, when other parameters are known, the following formulas are used to find the area of a triangle:
- Area of a scalene triangle = \(\sqrt {s(s - a)(s - b)(s - c)}\); where a, b, and c are the sides and 's' is the semi-perimeter; s = (a + b + c)/2
- Area of triangle = 1/2 × side 1 × side 2 × sin(θ); when 2 sides and the included angle is known, where θ is the angle between the given two sides.
- Area of an equilateral triangle = (√3)/4 × side2
- Area of an isosceles triangle = 1/4 × b\(\sqrt {4{a^2} - {b^2}}\); where 'b' is the base and 'a' is the length of an equal side.
How to Find the Base and Height of a Triangle?
The area of the triangle is calculated with the formula: A = 1/2 (base × height). Using the same formula, the height or the base can be calculated when the other dimensions are known. For example, if the area and the base of the triangle is known then the height can be calculated as, Height of the triangle = (2 × Area)/base. Similarly, when the height and the area is known, the base can be calculated with the formula, Base of the triangle = (2 × Area)/height
How to Find the Area and Perimeter of a Triangle?
The area of a triangle can be calculated with the help of the formula: A = 1/2 (b × h). The perimeter of a triangle can be calculated by adding the lengths of all the three sides of the triangle.
How to Find the Area of a Triangle Without Height?
The area of a triangle can be calculated when only the length of the 3 sides of the triangle are known and the height is not given. In this case, the Heron's formula can be used to find the area of the triangle. Heron's formula: A = \(\sqrt {s(s - b)(s - b)(s - c)}\) where a, b, and c are the sides of the triangle and 's' is the semi-perimeter; s = (a + b + c)/2.
How to Find the Area of Triangle with Two Sides and an Included Angle?
In a triangle, when two sides and the included angle is given, then the area of the triangle is half the product of the two sides and sine of the included angle. For example, In ∆ABC, when sides 'b' and 'c' and included angle A is known, the area of the triangle is calculated with the help of the formula: 1/2 × b × c × sin(A). For a detailed explanation refer to the section, 'Area of Triangle With 2 Sides and Included Angle (SAS)', given on this page.
How to Find the Area of a Triangle with 3 Sides?
The area of a triangle with 3 sides can be calculated using Heron's formula. Heron's formula: A = \(\sqrt {s(s - a)(s - b)(s - c)}\) where a, b, and c are the sides of the triangle and 's' is the semi-perimeter; s = (a + b + c)/2.
What is the Formula to Calculate the Area of a Triangle?
The formula for the area of a triangle depends on the dimensions that are known and also on the type of the triangle. There are different formulas for different types of triangles given above on this page in detail. A few of them are listed below.
- Area of a scalene triangle = \(\sqrt {s(s - a)(s - b)(s - c)}\); where a, b, and c are the sides and 's' is the semi-perimeter; s = (a + b + c)/2
- Area of an equilateral triangle = (√3)/4 × side2
- Area of an isosceles triangle = 1/4 × b\(\sqrt {4{a^2} - {b^2}}\); where 'b' is the base and 'a' is the length of an equal side.