Area of a Circle
The area of a circle is the space occupied by the circle in a two-dimensional plane. Alternatively, the space occupied within the boundary/circumference of a circle is called the area of the circle. The formula for the area of a circle is A = πr2, where r is the radius of the circle. The unit of area is the square unit, for example, m2, cm2, in2, etc.
The area of a circle formula is useful for measuring the region occupied by a circular field or a plot. Suppose, if you have a circular table, then the area formula will help us to know how much cloth is needed to cover it completely. Does a circle have volume? No, a circle doesn't have a volume. A circle is a two-dimensional shape, it does not have volume. A circle only has an area and perimeter/circumference. Let us learn in detail about the area of a circle, surface area, and its circumference with examples.
What is the Area of Circle?
The area of a circle is the amount of space enclosed within the boundary of a circle. The region within the boundary of the circle is the area occupied by the circle. It may also be referred to as the total number of square units inside that circle. Area of Circle = πr2 or πd2/4 in square units, where
- (Pi) π = 22/7 or 3.14.
- r = radius of the circle
- d = diameter of the circle
Pi (π) is the ratio of circumference to diameter of any circle. It is a special mathematical constant.
Circle and Parts of a Circle
Let us recall the circle and its parts before learning about area of circle in detail. A circle is a collection of points that are at a fixed distance from the center of the circle. A circle is a closed geometric shape. We see circles in everyday life such as a wheel, pizzas, a circular ground, etc. The measure of the space or region enclosed inside the circle is known as the area of the circle.

Radius: The distance from the center to a point on the boundary is called the radius of a circle. It is represented by the letter 'r' or 'R'. Radius plays an important role in the formula for the area and circumference of a circle, which we will learn later.
Diameter: A line that passes through the center and its endpoints lie on the circle is called the diameter of a circle. It is represented by the letter 'd' or 'D'.
Diameter formula: The diameter formula of a circle is twice its radius. Diameter = 2 × Radius. d = 2r or D = 2R. If the diameter of a circle is known, its radius can be calculated as: r = d/2 or R = D/2.
Circumference: The circumference of the circle is equal to the length of its boundary. This means that the perimeter of a circle is also referred to as its circumference. The length of the rope that wraps around the circle's boundary perfectly will be equal to its circumference. The below-given figure helps you visualize the same. The circumference can be measured by using the given formula:

where 'r' is the radius of the circle and π is the mathematical constant whose value is approximated to 3.14 or 22/7. For a circle with radius ‘r’ and circumference ‘C’:
- π = Circumference/Diameter
- π = C/2r = C/d
- C = 2πr
Let us understand the different parts of a circle using the following real-life example.
Consider a circular-shaped park as shown in the figure below. We can identify the various parts of a circle with the help of the figure and table given below.

| In a Circle | In our park | Named by the letter |
|---|---|---|
| Centre | Fountain | F |
| Circumference | Boundary | |
| Chord | Play area entrance | PQ |
| Radius | Distance from the fountain to the Entrance gate | FA |
| Diameter | Straight Line Distance between Entrance Gate and Exit Gate through the fountain | AFB |
| Minor segment | The smaller area of the park, which is shown as the Play area | |
| Major segment | The bigger area of the park, other than the Play area | |
| Interior part of the circle | The green area of the whole park | |
| Exterior part of the circle | The area outside the boundary of the park | |
| Arc | Any curved part on the circumference. |
Area of Circle Formulas
The area of a circle can be calculated in intermediate steps from the diameter, and the circumference of a circle. From the diameter and the circumference, we can find the radius and then find the area of a circle. But these formulae provide the shortest method to find the area of a circle. Suppose a circle has a radius 'r' then the area of circle = πr2 or πd2/4 in square units, where π = 22/7 or 3.14, and d is the diameter.
Area of a circle, A = πr2 square units
Circumference / Perimeter = 2πr units
Area of a circle can be calculated by using the formulas:
- Area = π × r2, where 'r' is the radius.
- Area = (π/4) × d2, where 'd' is the diameter.
- Area = C2/4π, where 'C' is the circumference (sometimes referred to as perimeter).
Examples using Area of Circle Formula
Let us consider the following illustrations based on the area of circle formula.
Example 1: If the length of the radius of a circle is 4 units. Calculate its area.
Solution:
Radius(r) = 4 units(given)
Using the formula for the circle's area,
Area of a Circle = πr2
Put the values,
A = π(4)2
A =π × 16
A = 16π ≈ 50.27
Answer: The area of the circle is 50.27 squared units.
Example 2: The length of the largest chord of a circle is 12 units. Find the area of the circle.
Solution:
Diameter(d) = 12 units(given)
Using the formula for the circle's area,
Area of a Circle = (π/4)×d2
Put the values,
A = (π/4) × 122
A = (π/4) × 144
A = 36π ≈ 113.1
Note: Alternatively, we can find the radius(r) first and then apply πr2 formula.
Answer: The area of the circle is 113.1 square units.
Area of a Circle Using Diameter
The area of the circle formula in terms of the diameter is: Area of a Circle = πd2/4. Here 'd' is the diameter of the circle. The diameter of the circle is twice the radius of the circle. d = 2r. Generally from the diameter, we need to first find the radius of the circle and then find the area of the circle. With this formula, we can directly find the area of the circle, from the measure of the diameter of the circle as shown in the above example.

Area of a Circle Using Circumference
The circumference of a circle can be used to find the area of that circle. The area of a circle formula in terms of the circumference is given by the formula \(\dfrac{(Circumference)^2}{4\pi}\). There are usually two simple steps to find the area of a circle from the given circumference of a circle. The circumference of a circle is first used to find the radius of the circle. This radius is further helpful to find the area of a circle. But using this formula, we will be able to directly find the area of a circle from the circumference of the circle.

Area of a Circle-Calculation
The area of the circle can be conveniently calculated either from the radius, diameter, or circumference of the circle. The constant used in the calculation of the area of a circle is pi, and it has a fractional numeric value of 22/7 or a decimal value of 3.14. Any of the values of pi can be used based on the requirement and the need of the equations. The below table shows the list of formulae if we know the radius, the diameter, or the circumference of a circle.
| Area of a circle when the radius is known. | πr2 |
|---|---|
| Area of a circle when the diameter is known. | πd2/4 |
| Area of a circle when the circumference is known. | C2/4π |
Derivation of Area of a Circle
Why is the area of the circle is πr2? To understand this, let's first understand how the formula for the area of a circle is derived.
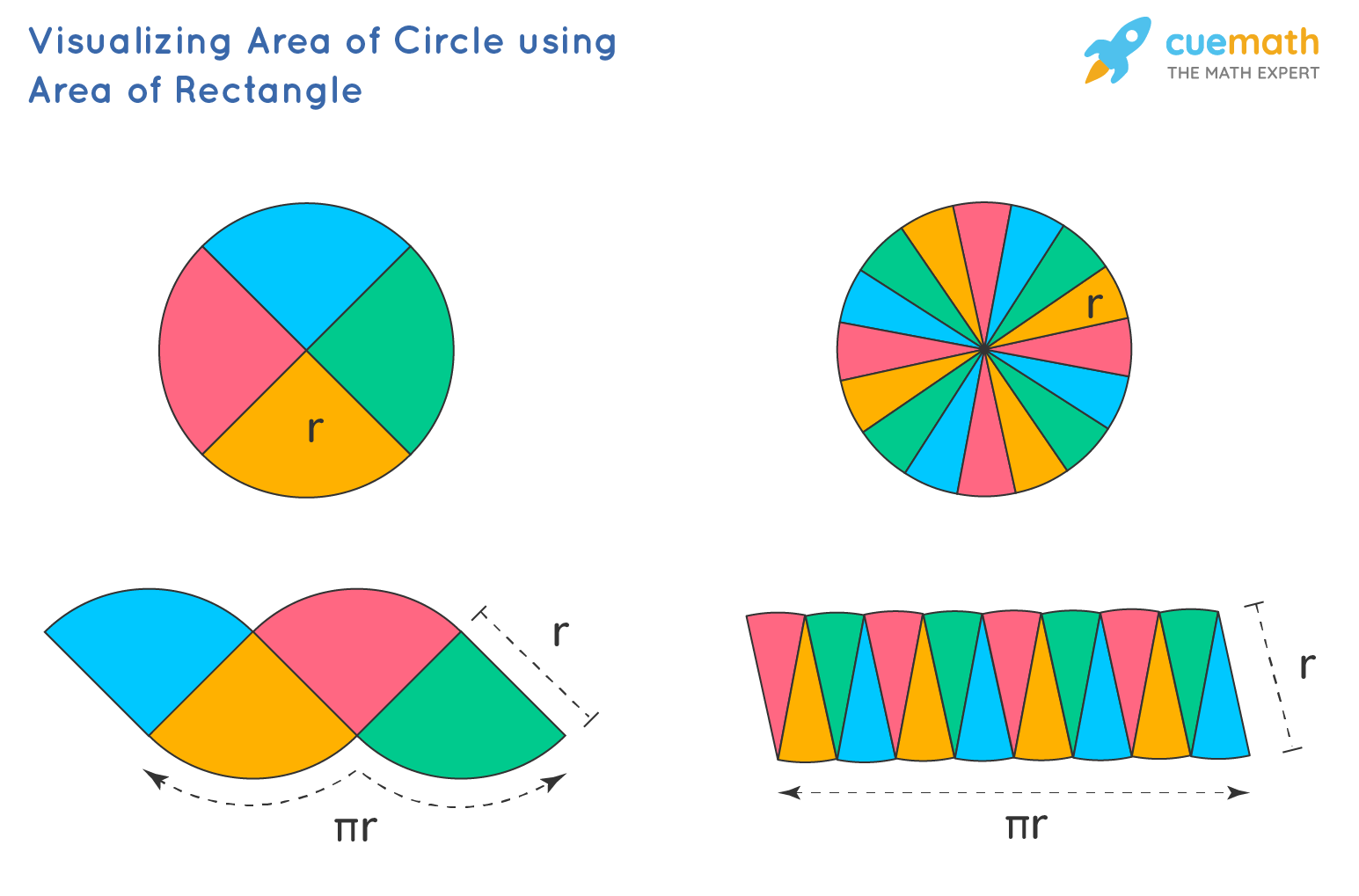
Observe the above figure carefully, if we split up the circle into smaller sections and arrange them systematically it forms a shape of a parallelogram. When the circle is divided into even smaller sectors, it gradually becomes the shape of a rectangle. The more the number of sections it has more it tends to have a shape of a rectangle as shown above.
The area of a rectangle is = length × breadth
The breadth of a rectangle = radius of a circle (r)
When we compare the length of a rectangle and the circumference of a circle we can see that the length is = ½ the circumference of a circle
Area of circle = Area of rectangle formed = ½ (2πr) × r
Therefore, the area of the circle is πr2, where r, is the radius of the circle and the value of π is 22/7 or 3.14.
Surface Area of Circle Formula
The surface area of a circle is the same as the area of a circle. In fact, when we say the area of a circle, we mean nothing but its total surface area. Surface area is the area occupied by the surface of a 3-D shape. The surface of a sphere will be spherical in shape but a circle is a simple plane 2-dimensional shape. So technically, we don't use the phrase "surface area" to refer to the area of a circle, instead, we just call it as "area of circle".
If the length of the radius or diameter or even the circumference of the circle is given, then we can find out the surface area. It is represented in square units. The surface area of circle formula = πr2 where 'r' is the radius of the circle and the value of π is approximately 3.14 or 22/7.
Differences Between Area and Circumference of a Circle
Here are some important differences between circumference (perimeter) and area of a circle.
| Circumference (C) | Area (A) | |
|---|---|---|
| Definition | The length of circle's boundary. | The amount of space within the circle. |
| Units | Same length as unit. Example: cm, in, ft, etc. | It is measured in square units. Example: cm2, in2, ft2, etc. |
| Formula | 2πr | πr2 |
| Relationship With Radius | Circumference is directly proportional to the radius. | The area is directly proportional to the square of the radius. |
| Relationship With Diameter | Circumference is directly proportional to the diameter. | The area is directly proportional to the square of the diameter. |
Real-World Example on Area of Circle
Ron and his friends ordered a pizza on Friday night. Each slice was 15 cm in length.
Calculate the area of the pizza that was ordered by Ron. You can assume that the length of the pizza slice is equal to the pizza’s radius.
Solution:
A pizza is circular in shape. So we can use the area of a circle formula to calculate the area of the pizza. Radius is 15 cm.
Area of Circle formula = πr2 = 3.14 × 15 × 15 = 706.5
Area of the Pizza = 706.5 sq. cm.
☛ Related Topics:
- Circle Calculator
- Radius of Circle Calculator
- Circumference of Circle Calculator
- Area of a Circle Calculator
Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12. Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.
Area of Circle Examples
-
Example 1: Find the circumference and the area of a circle whose radius is 14 cm.
Solution:
Given: Radius of the circle = 14 cm
Circumference of the Circle = 2πr
= 2 × 22/7 × 14
= 2 × 22 × 2
= 88 cm
Using area of Circle formula = πr2
= 22/7 × 14 × 14
= 22 × 2 × 14
= 616 sq. cm.
Area of the Circle = 616 sq. cm.
Answer: Circumference = 88 cm and area = 616 sq. cm.
-
Example 2: The ratio of the area of 2 circles is 4:9. With the help of the area of circle formula find the ratio of their radii.
Solution:
Let us assume the following:
The radius of the 1st circle = R1
Area of the 1st circle = A1
The radius of the 2nd circle = R2
Area of the 2nd circle = A2
It is given that A1:A2 = 4:9
Area of a Circle = πr2
π\(R_1\)2 : π\(R_2\)2 = 4 : 9
Taking square roots of both sides,
R1 : R2 = 2 : 3
Answer: The ratio of the radii = 2:3
-
Example 3: A race track is in the form of a circular ring. The inner radius of the track is 58 yd and the outer radius is 63 yd. Find the area of the race track.
Solution:
Given: R = 63 yd, r = 56 yd.
Let the area of the outer circle be A1 and the area of the inner circle be A2
Area of race track = A1 - A2 = πR2 - πr2 = π(632 - 562) = 22/7 × 833 = 2,618 square yards.
Answer: The area of the race track is 2618 square yards.
-
Example 4: A wire is in the shape of an equilateral triangle. Each side of the triangle measures 7 in. The wire is bent into the shape of a circle. Find the area of the circle that is formed.
Solution:
Perimeter of the Equilateral Triangle: Perimeter of the triangle = 3 × side = 3 × 7 = 21 inches.
Since the perimeter of the equilateral triangle = Circumference of the circle formed.
Thus, the perimeter of the triangle is 21 inches.
Circumference of a Circle = 2πr = 2 × 22/7 × r = 21
r = (21 × 7)/(44) = 3.34.
Therefore, the Radius of the circle is 3.34 cm. Area of a circle = πr2 = 22/7 ×(3.34)2 = 35.042 square inches.
Answer: The area of a circle is 35.042 square inches.
-
Example 5: The time shown in a circular clock is 3:00 pm. The length of the minute hand is 21 units. Find the distance travelled by the tip of the minute hand when the time is 3:30 pm.
Solution:
When the minute hand is at 3:30 pm, it covers half of the circle. So, the distance travelled by the minute hand is actually half of the circumference. Distance \(= \pi\) (where r is the length of the minute hand). Hence the distance covered = 22/7 × 21 = 22 × 3 = 66 units.
Answer: The distance travelled is 66 units.

FAQs on Area of Circle
How to Calculate the Area of a Circle?
The area of circle can be calculated if we know either the radius (r) , the diameter (d), or the circumference (C) using one of the following formulas:
- Area = π × r2
- Area = (π/4) × d2
- Area = C2/4π
What Is the Area of Circle Formula?
Area of circle formula = π × r2. The area of a circle is π multiplied by the square of the radius. The area of a circle when the radius 'r' is given is πr2. The area of a circle when the diameter 'd' is known is πd2/4. π is approx. 3.14 or 22/7. Area(A) could also be found using the formulas A = (π/4) × d2, where 'd' is the radius and A= C2/4π, where 'C' is the given circumference.
What Is the Perimeter and Area of a Circle?
The circumference of the circle is equal to the length of its boundary. This means that the perimeter of a circle is equal to its circumference. The area of a circle is πr2 and the perimeter (circumference) is 2πr when the radius is 'r' units, π is approx 3.14 or 22/7. The circumference and the radius length of a circle are important parameters to find the area of that circle. For a circle with radius ‘r’ and circumference ‘C’:
- π = Circumference ÷ Diameter
- π = C/2r
- Therefore, C = 2πr
Why Is the Area of a Circle Formula is πr2?
A circle can be divided into many small sectors which can then be rearranged accordingly to form a parallelogram. When the circle is divided into even smaller sectors, it gradually becomes the shape of a rectangle. We can clearly see that one of the sides of the rectangle will be the radius and the other will be half the length of the circumference, i.e, π. As we know that the area of a rectangle is its length multiplied by the breadth which is π multiplied to 'r'. Therefore, the area of the circle is πr2.
What Is the Area of a Circle Formula in Terms of π?
The value of pi (π) is approximately 3.14. Pi is an irrational number. This means that its decimal form neither ends (like 1/5 = 0.2) nor becomes repetitive (like 1/3 = 0.3333...). Pi is 3.141592653589793238... (to only 18 decimal places). Hence the area of a circle formula in terms of pi is given as πr2 square units.
How Do You Find the Circumference and Area of a Circle?
The area and circumference of a circle can be calculated using the following formulas. Circumference = 2πr ; Area = πr2. The circumference of the circle can be taken as π times the diameter of the circle. And the area of the circle is π times the square of the radius of the circle.
How to Calculate the Area of a Circle With Diameter?
The diameter of the circle is double the radius of the circle. Hence the area of the circle formula using the diameter is equal to π/4 times the square of the diameter of the circle. The formula for the area of the circle, using the diameter of the circle π/4 × diameter2.
How Do You Find the Area of a Circle Given the Circumference?
The area of a circle can also be found using the circumference of the circle. The radius of the circle can be found from the circumference of the circle and this value can be used to find the area of the circle. Assume that the circumference of the circle is 'C'. We have C = 2πr, or r = C/2π. Now applying this 'C' value in the Area formula we have A = πr2 = π × (C/2π)2 = C2/4π.
What are Area and Perimeter of Circle Formulas?
For a circle of radius 'r':
What Is the Area of Circle Inscribed in a Square of Length 6 m?
When a circle is inscribed inside a square, then the diameter of the circle = side length of the square = 6 m. Then its radius = 3 m. Therefore, the area of the circle inscribed in the given square = 3.14 × 3 × 3 = 28.26 sq. m.
The Circumference of a Given Circle Is 16 cm. What Will Be Its Area?
Circumference of a circle = 16 cm
We know the formula of circumference, C =2πr
So,
2πr = 16
or r = 16/2π = 8/π
Substituting the value of 'r' in the area of circle formula, we get:
A = πr2
A = π(8/π)2 = 64/π
On solving,
Area = 20.38 sq. cm.
What is the Ratio of Diameter to Area of a Circle?
Consider a circle of radius 'r'. Then its diameter = 2r ad its area = πr2. Then the ratio of diameter to area is = 2r : πr2 = 2 : πr.
visual curriculum