Arc Length
Arc length is better defined as the distance along the part of the circumference of any circle or any curve (arc). Any distance along the curved line that makes up the arc is known as the arc length. A part of a curve or a part of a circumference of a circle is called Arc. All of them have a curve in their shape. The length of an arc is longer than any straight line distance between its endpoints (a chord).
In particular, the length of an arc of a circle of radius 'r' that subtends an angle θ at the center is calculated by the formula rθ × (π/180) if the angle is in degrees and if the angle is in radians, then the arc length is rθ. Let 's see how to derive these formulas.
| 1. | What is Arc Length? |
| 2. | Arc Length Formula |
| 3. | How to Find Arc Length of a Curve? |
| 4. | FAQs on Arc Length |
What is Arc Length?
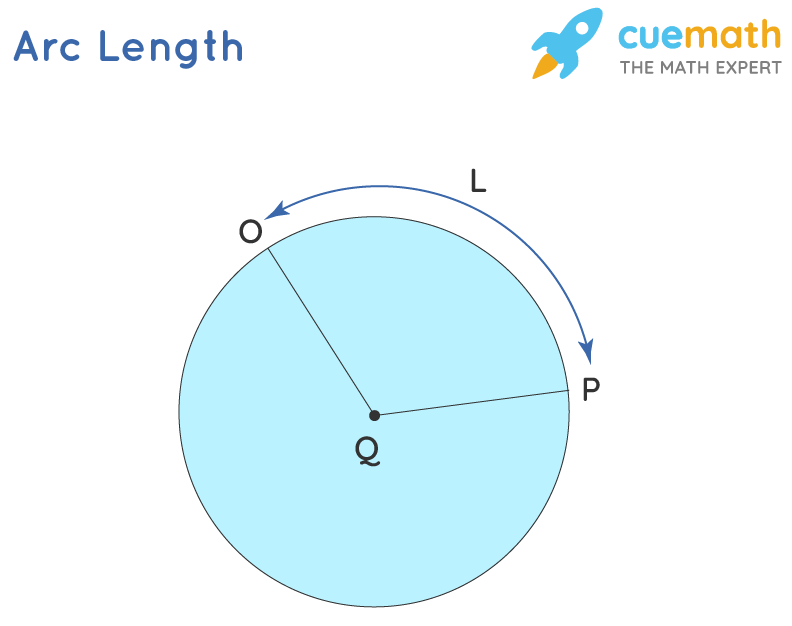
The arc length is defined as the interspace between the two points along a section of a curve. An arc of a circle is any part of the circumference. The angle subtended by an arc at any point is the angle formed between the two line segments joining the center to the end-points of the arc. For example, in the circle shown below, OP is the arc of the circle with center Q. The arc length of this arc OP is given as L.
Arc Length Formula
To derive the arc length formula, let us recall what is the circumference of a full circle whose radius is 'r'. It is 2πr. But arc is just a part (in fact a fraction) of the total circumference. We know that the angle at the center in a full circle is 360°. If the angle subtended by an arc is θ°, then it means that the arc occupies a fraction of θ/360 out of the total circumference. Thus:
Arc length = θ/360 of 2πr = θ/360 × 2πr = rθ × π/180.
This is the arc length formula when the angle is in degrees. The length of an arc can be calculated using different formulas, based on the unit of the central angle of the arc. The measurements of the central angle can be given in degrees or radians, and accordingly, we calculate the arc length of a circle.
If θ is in radians, then the angle in degrees = θ × 180/π. By substituting this in the above formula,
Arc length = rθ × π/180 × 180/π = rθ.
Thus, the arc of a circle formula is θ times the radius of a circle, if the angle is in radians.
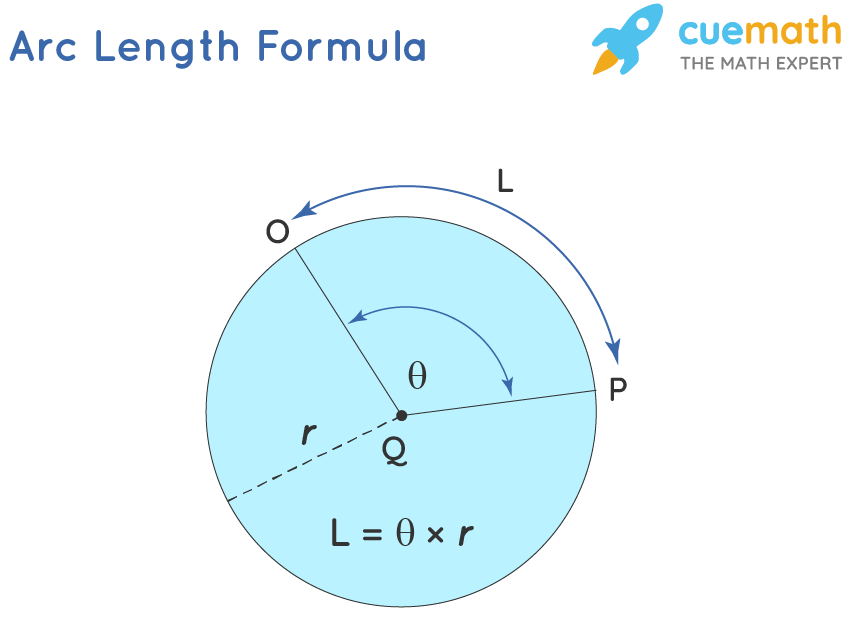
The arc length formula can be expressed as:
arc length, L = θ × r, when θ is in radian;
arc length, L = θ × (π/180) × r, where θ is in degrees,
where,
- L = Length of an Arc
- θ = Central angle of Arc
- r = Radius of the circle
Arc Length Formula in Radians
The arc length of a circle can be calculated using different formulas, based on the unit of the center angle of the arc. The arc length formula in radians can be expressed as,
Arc Length = θ × r
where,
- L = Arc Length
- θ = Center angle of the arc in radians
- r = Radius of the circle
How to Find Arc Length of a Curve?
The arc length of an arc of a circle can be calculated using different methods and formulas based on the given data. Some important cases are given below,
- find arc length with the radius and central angle
- find arc length without the radius
- find arc length without the central angle
How to Find Arc Length With the Radius and Central Angle?
The arc length of a circle can be calculated with the radius and central angle using the arc length formula,
- Length of an Arc = θ × r, where θ is in radian.
- Length of an Arc = θ × (π/180) × r, where θ is in degree.
How to Find Arc Length Without the Radius?
The arc length of a circle can be calculated without the radius using:
Central angle and the sector area:
- The sector area formula is, (θ/360º) × πr2, if θ is in degrees (or) (1/2) r2θ, if θ is in radians.
- Use this formula and solve for the radius 'r'. We need to use the square root in this process.
- Then find the arc length using the relevant formula.
Example: Calculate the arc length of a curve with sector area 25 square units and the central angle as 2 radians.
We have,
Sector area = 25 units
Central angle = 2 radians
- Step 1: Sector area = 25 ⇒ (1/2) r2(2) = 25
- Step 2: This gives r2 = 25. By taking square root on both sides, r = 5.
- Step 3: Arc length = rθ = 5 × 2 = 10 units
Thus, arc length = 10 units
Central angle and the chord length:
- The chord length formula is, 2r sin (θ/2).
- Use this formula and solve for the radius 'r'.
- Then its easy to find the arc length using the suitable formula.
Example: Calculate the arc length of a curve, whose endpoints touch a chord of the circle measuring 5 units. The central angle subtended by the arc is 2 radians.
We have,
Chord length = 5 units
Central angle = 2 radians
- Step 1: Chord length = 5 ⇒ 2r sin (2/2) = 5
- Step 2: 2r sin (1) = 5 ⇒ r = 5 / (2 × sin 1) = 2.97 units
- Step 3: Arc length = radius × central angle = 2.97 × 2 = 5.94 units
Thus, arc length = 5.94 units
How to Find Arc Length Without the Central Angle?
The arc length of a circle can be calculated without the angle using:
Radius and the sector area:
- Substitute the values of radius and sector area in the formula of sector area.
- Solve it for the central angle.
- Find the arc length.
Example: Calculate the arc length of a curve with a sector area 25 square units and radius as 2 units.
We have,
Sector area = 25 units
Central angle = 2 units
- Step 1: Sector area = 25 ⇒ (1/2) (2)2θ = 25.
- Step 2: Solving the above equation, we get θ = 12.5 radians.
- Step 3: Arc length = radius × central angle = 2 × 12.5 = 25 units
Thus, arc length = 25 units
Radius and chord length:
- Substitute the values of radius and chord length in the formula of chord length.
- Then solve for the central angle.
- Calculate the arc length.
Example: Calculate the arc length of a curve, whose endpoints touch a chord of the circle measuring 3 units. The radius of the circle is 2 units.
We have,
Chord length = 5 units
Central angle = 2 units
- Step 1: Chord length = 3 ⇒ 2(2) sin (θ/2) = 3
- Step 2: Solving this, we get: sin (θ/2) = 0.75 ⇒ θ/2 = sin-1(0.75) = 0.848 ⇒ θ = 1.696.
- Step 3: Arc length = radius × central angle = 2 × 1.696 = 3.392 units
Thus, arc length = 3.392 units
☛ Important Notes on Arc of a Circle:
Given below are key highlights on the concept of arc length.
- Arc Length = θ × r, where θ is in radians.
- Arc Length = θ × (π/180) × r, where θ is in degrees.
☛ Related Topics on Arc Length
Check out a few more interesting articles related to arc length to understand the topic more precisely.
Examples on Arc length
-
Example 1: Find the length of an arc of a circle cut off by a central angle of 4 radians in a circle with a radius of 6 inches.
Solution:
Center angle, θ = 4 radians, radius, r = 6 inches. Use the arc length formula, L = θ × r = 4 × 6 = 24 inches.
Answer: ∴ Arc length (PQ) = 24 inches
-
Question 2: The radius of the circle is 14 units and the arc subtends 65° at the center. What is the length of the arc using circumference?
Solution: We know that,
Circumference of circle = 2πr
C = 2π × 14 = 28π
arc length = (θ/360) × C = (65°/360°)28π = 15.882 units
Answer: Arc length = 15.882 units.
-
Example 3: Calculate the length of an arc cut off by a central angle, θ = 40º in a circle with a radius of 4 inches.
Solution:
Radius, r = 4 inches , θ = 40º. Use the arc length formula, L = π × (r) × (θ/180º) = π × (4) × (40º/180º) = 2.79 inches.
Answer: ∴ The length of the arc of the given circle = 2.79 inches

FAQs on Arc Length
What is Arc of a Circle?
The arc of a circle is defined as the length of a part of its circumference that lies between any two points on it. i.e., An arc of a circle is any part of the circumference. The angle subtended by an arc at any point is the angle formed between the two line segments joining that point to the end-points of the arc.
What is the Arc Length of a Circle Formula?
The arc length of a circle formula involves its radius (r) and the central angle (θ). It is denoted by L and is calculated by
- the formula L = rθ × (π/180) if θ is in degrees
- the formula using L = rθ if θ is in radians
How do you Find the Length of an Arc Without the Radius?
To find the arc length, we definitely need the radius of the circle and central angle. But when the radius is not given, then either the sector area or the chord length might have been given. Use the following formulas to solve for the radius and then apply the arc length formula.
- Sector area = (θ/360º) × πr2, if θ is in degrees (or) (1/2) r2θ
- Chord length = 2r sin (θ/2)
What do You Understand By Arc Length Equation?
There are two equations associated with arc length. Given below are the two arc length equations.
- Arc Length = θ × r, where θ is in radian.
- Arc Length = rθ × (π/180), where θ is in degree
How to Calculate Arc Length Using Radians?
The arc length can be calculated when the central angle is given in radians using the arc of a circle formula: Arc Length = θ × r, when θ is in radian.
- L = Arc Length
- θ = Center angle of the arc
- r = Radius of the circle
Does Arc Length have to be in Radians?
No, arc length cannot be in radians. It is a measurement of distance, so cannot be in radians. The central angle subtended at the center can be in radians, degrees, or arcsecs accordingly.
How do you Find the Circumference of Arc?
When arc length (L) is given with central angle θ then the circumference (C) is calculated using the equation L / C = θ/360º.
What is the Length of Major Arc Using Arc Length Formula?
A major arc in a circle is larger than a semicircle. Iis central angle is larger than 180°. Using formula ℓ = rθ we can find the length of an arc of a circle, where θ is in radians.
visual curriculum