Square Root
The square root of a number is the inverse operation of squaring a number. The square of a number is the value that is obtained when we multiply the number by itself, while the square root of a number is obtained by finding a number that when squared gives the original number.
If 'a' is the square root of 'b', it means that a × a = b. The square of any number is always a positive number, so every number has two square roots, one of a positive value, and one of a negative value. For example, both 2 and -2 are square roots of 4. However, in most places, only the positive value is written as the square root of a number.
What is Square Root?
The square root of a number is that factor of a number which when multiplied by itself gives the original number. Squares and square roots are special exponents. Consider the number 9. When 3 is multiplied by itself, it gives 9 as the product. This can be written as 3 × 3 or 32. Here, the exponent is 2, and we call it a square. Now when the exponent is 1/2, it refers to the square root of the number. For example, √n = n1/2, where n is a positive integer.
Square Root Definition
The square root of a number is the value of power 1/2 of that number. In other words, it is the number whose product by itself gives the original number. It is represented using the symbol '√ '. The square root symbol is called a radical, whereas the number under the square root symbol is called the radicand.
How to Find Square Root?
To find the square root of a number, we just see by squaring which number would give the actual number. It is very easy to find the square root of a number that is a perfect square. Perfect squares are those positive numbers that can be expressed as the product of a number by itself. In other words, perfect squares are numbers which are expressed as the value of power 2 of any integer. We can use four methods to find the square root of numbers and those methods are as follows:
- Repeated Subtraction Method
- Prime Factorization Method
- Estimation Method
- Long Division Method
It should be noted that the first three methods can be conveniently used for perfect squares, while the fourth method, i.e., the long division method can be used for any number whether it is a perfect square or not.
Repeated Subtraction Method of Square Root
This is a very simple method. We subtract the consecutive odd numbers from the number for which we are finding the square root, till we reach 0. The number of times we subtract is the square root of the given number. This method works only for perfect square numbers. Let us find the square root of 16 using this method.
- 16 - 1 = 15
- 15 - 3 =12
- 12 - 5 = 7
- 7- 7 = 0
You can observe that we have subtracted 4 times. Thus,√16 = 4
Square Root by Prime Factorization Method
Prime factorization of any number means to represent that number as a product of prime numbers. To find the square root of a given number through the prime factorization method, we follow the steps given below:
- Step 1: Divide the given number into its prime factors.
- Step 2: Form pairs of factors such that both factors in each pair are equal.
- Step 3: Take one factor from the pair.
- Step 4: Find the product of the factors obtained by taking one factor from each pair.
- Step 5: That product is the square root of the given number.
Let us find the square root of 144 by this method.

This method works when the given number is a perfect square number.
Finding Square Root by Estimation Method
Estimation and approximation refer to a reasonable guess of the actual value to make calculations easier and more realistic. This method helps in estimating and approximating the square root of a given number. Let us use this method to find √15. Find the nearest perfect square number to 15. 9 and 16 are the perfect square numbers nearest to 15. We know that √16 = 4 and √9 = 3. This implies that √15 lies between 3 and 4. Now, we need to see if √15 is closer to 3 or 4. Let us consider 3.5 and 4. Since 3.52 = 12.25 and 42= 16. Thus, √15 lies between 3.5 and 4 and is closer to 4.
Let us find the squares of 3.8 and 3.9. Since 3.82 = 14.44 and 3.92 = 15.21. This implies that √15 lies between 3.8 and 3.9. We can repeat the process and check between 3.85 and 3.9. We can observe that √15 = 3.872.
This is a very long process and time-consuming.
Calculating Square Root by Long Division Method
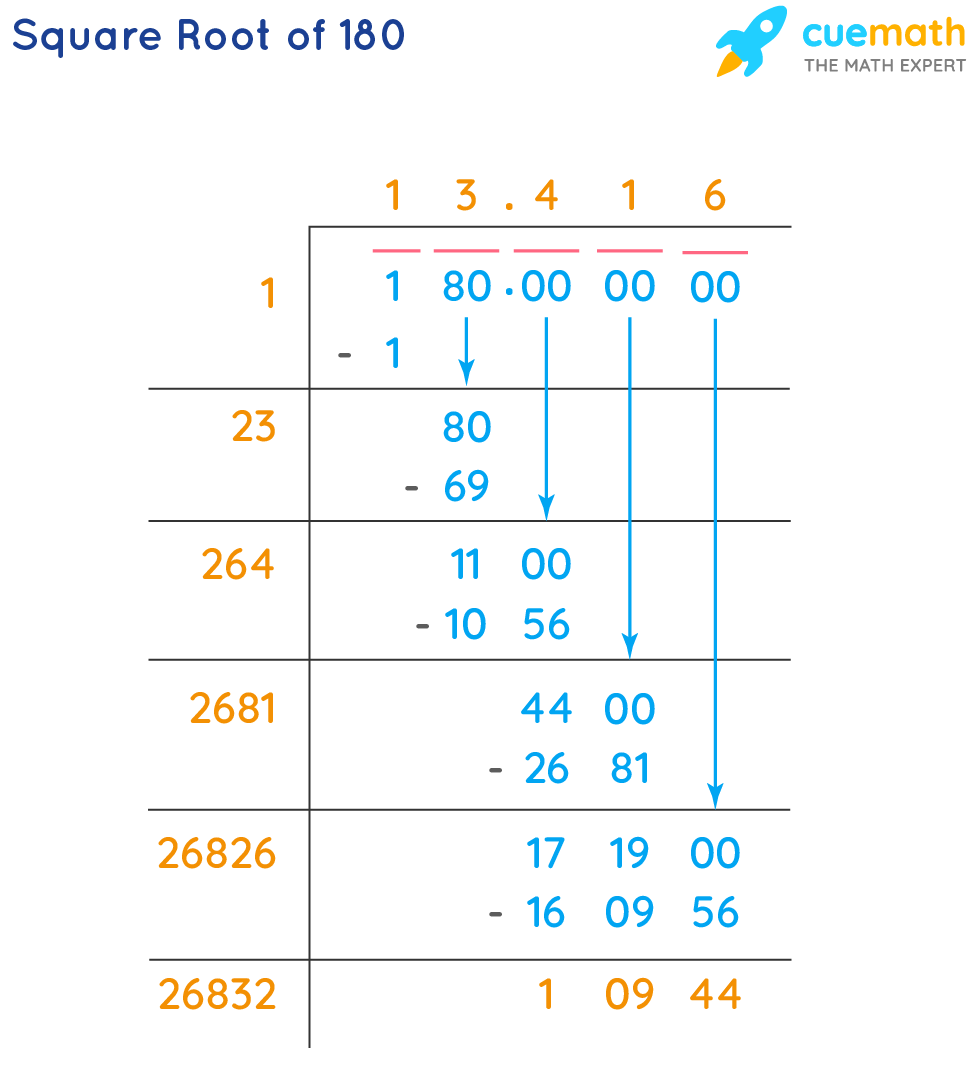
Long division is a method for dividing large numbers into steps or parts, breaking the division problem into a sequence of easier steps. We can find the exact square root of any given number using this method. Let us understand the process of finding square root by the long division method with an example. Let us find the square root of 180.
- Step 1: Place a bar over every pair of digits of the number starting from the units' place (right-most side). We will have two pairs, i.e., 1 and 80
- Step 2: We divide the left-most number by the largest number whose square is less than or equal to the number in the left-most pair.

Step 3: Bring down the number under the next bar to the right of the remainder. Add the last digit of the quotient to the divisor. To the right of the obtained sum, find a suitable number which, together with the result of the sum, forms a new divisor for the new dividend that is carried down.

Step 4: The new number in the quotient will have the same number as selected in the divisor. The condition is the same — as being either less than or equal to the dividend.
Step 5: Now, we will continue this process further using a decimal point and adding zeros in pairs to the remainder.

Step 6: The quotient thus obtained will be the square root of the number. Here, the square root of 180 is approximately equal to 13.4 and more digits after the decimal point can be obtained by repeating the same process as follows.
Square Root Table
The square root table consists of numbers and their square roots. It is useful to find the squares of numbers as well. Here is the list of square roots of perfect square numbers and some non-perfect square numbers from 1 to 10.
| Number | Square Root |
|---|---|
| 1 | 1 |
| 2 | 1.414 |
| 3 | 1.732 |
| 4 | 2 |
| 5 | 2.236 |
| 6 | 2.449 |
| 7 | 2.646 |
| 8 | 2.828 |
| 9 | 3 |
| 10 | 3.162 |
The numbers that are not perfect squares are irrational numbers.
Square Root Formula
The square root of a number has the exponent of 1/2. The square root formula is used to find the square root of a number. We know the exponent formula: \(\sqrt[\text{n}]{x}\) = x1/n. When n = 2, we call it square root. We can use any of the above methods for finding the square root, such as prime factorization, and so on. 91/2 = √9 = √(3×3) = 3. So, the formula for writing the square root of a number is √x= x1/2.
Simplifying Square Root
To simplify a square root, we need to find the prime factorization of the given number. If a factor doesn't have a pair, retain them under the square root symbol, otherwise, take one number out of the square root from each pair. For example: √12 = \(\sqrt{2 \times 2\times3}\) = 2√3. This is because the rule of simplifying square root is √xy = √(x × y), where, x and y are positive integers.
For fractions, there is also a similar rule: √x/√y = √(x/y). For example: √50/√10 = √(50/10)= √5
Square Root of a Negative Number
The square root of a negative number cannot be a real number, since a square is either a positive number or zero. But complex numbers have the solutions to the square root of a negative number. The principal square root of -x is: √(-x)= i√x. Here, i is the square root of -1.
For example: Take a perfect square number like 16. Now, let's see the square root of -16. There is no real square root of -16. √(-16)= √16 × √(-1) = 4i (as, √(-1)= i), where 'i' is represented as the square root of -1. So, 4i is a square root of -16.
Square of a Number
Any number raised to exponent two (y2) is called the square of the base. So, 52 or 25 is referred to as the square of 5, while 82 or 64 is referred to as the square of 8. We can easily find the square of a number by multiplying the number two times. For example, 52 = 5 × 5 = 25, and 82 = 8 × 8 = 64. When we find the square of a whole number, the resultant number is a perfect square. Some of the perfect squares we have are 4, 9, 16, 25, 36, 49, 64, and so on. The square of a number is always a positive number.
☛Also Check:
How to Find the Square of a Number?
The square of a number can be found by multiplying a number by itself. For single-digit numbers, we can use multiplication tables to find the square, while in the case of two or more than two-digit numbers, we perform multiplication of the number by itself to get the answer. For example, 9 × 9 = 81, where 81 is the square of 9. Similarly, 3 × 3 = 9, where 9 is the square of 3.

The square of a number is written by raising the exponent to 2. For example, the square of 3 is written as 32 and is read as "3 squared". Here are some examples:
- 42 = 4 × 4 = 16
- (-6)2 = -6 × -6 = 36
- (5/3)2 = 5/3 × 5/3 = 25/9
Squares and Square Roots
There is very strong relation between squares and square roots as each one of them is the inverse relation of the other. i.e., if x2 = y then x = √y. It can be simply remembered like this:
- When "square" is removed from one side of the equation, we get the square root on the other side. For example, 42 = 16 means, 4 = √16. This is also known as "taking square root on both sides".
- When "square root" is removed from one side of the equation, we get square on the other side. For example, √25 = 5 means, 25 = 52. This is also known as "squaring on both sides"
This logic helps in solving many equations in algebra. Consider the following example:
Example: Solve the equation √(2x + 3) = 10.
Solution:
Squaring on both sides of the equation would result in the cancellation of the square root on the left side.
2x + 3 = 102
2x + 3 = 100
2x = 97
x = 97/2 = 48.5
Here are more differences between squares and square roots.
| Squares | Square Roots | |
|---|---|---|
| Definition | The product of a number multiplied by itself. | It is the number which when multiplied by itself gives the original number. |
| Example | 72 = 49 | √49 = 7 |
| Symbol | Exponent (^) | Square root (√) |
| Result | Positive always. | Can be either positive or negative. |
| Domain | Set of all real numbers | Set of all non-negative real numbers. |
| Inverse | Inverse of square is square root. | Inverse of square root is square. |
☛ Related Articles
Square Root of Numbers
Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12. Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.
Examples on Square Root
-
Example 1: Find out the square root of 529 by the prime factorization method.
Solution:

We can see that, 529 = 23×23 ⇒ √529= 23
∴ √529= 23.
Answer: 23
-
Example 2: Calculate the square and square root of the following numbers.
a) Square root of 25 is ___
b) Square of 16 is ____
c) Square of 20 is ____
d) Square root of 400 is _____
Solution:
a) Square root of 25 is 5
5 × 5 = 25
√25 = 5
b) Square of 16 is = 16 × 16 = 256
c) Square of 20 is = 20 × 20 = 400
d) Square root of 400 is 20 as
20 × 20 = 400
√400 = 20.
Answer: a) 5 b) 256 c) 400 d) 20
-
Example 3: Determine the square root of 60.
Solution:
To find: the square root of 60
From prime factorization of 60, we get,
60 = 2 × 2 × 3 × 5
= (2)2 × 3 × 5
Using square root formula,
√60 = [(2)2 × 15 ]1/2
√60 = 2√15
Therefore, the square root of 60 = 2√15
Answer: 2√15

FAQs on Square Root
What is Square Root in Math?
The square root of a number is a number that when multiplied by itself gives the actual number. For example, 2 is the square root of 4, and this is expressed as √4 = 2. This means when 2 is multiplied by 2 it results in 4 and this can be verified as 2 × 2 = 4.
☛ Check:
- Square Root 1 to 10
- Square Root 1 to 20
- Square Root 1 to 25
- Square Root 1 to 30
- Square Root 1 to 50
- Square Root 1 to 100
How to Calculate the Square Root of a Number?
It is very easy to find the square root of a number that is a perfect square. For example, 9 is a perfect square, 9 = 3 × 3. So, 3 is the square root of 9 and this can be expressed as √9 = 3. The square root of any number, in general, can be found by using any of the four methods given below:
- Repeated Subtraction Method
- Prime Factorization Method
- Estimation and Approximation Method
- Long Division Method
Can Square Root be Negative?
Yes, the square root of a number can be negative. In fact, all the perfect squares like 4, 9, 25, 36, etc. have two square roots, one is a positive value and one is a negative value. For example, the square roots of 4 are -2 and 2. To verify this, we can see that (-2) × (-2) = 4. Similarly, the square roots of 9 are 3 and -3.
How to Find the Square Root of a Decimal Number?
The square root of a decimal number can be found by using the estimation method or the long division method. In the case of decimal numbers, we make pairs of whole number parts and fractional parts separately. And then, we carry out the process of long division in the same way as any other whole number.
What is the Square Root Symbol?
The symbol that is used to denote square root is called the radical sign '√ '. The term written inside the radical sign is called the radicand.
How to Multiply Two Square Root Values Together?
Let us say we have two numbers a and b. First, we will find the square root of the numbers a and b. Then, after finding the square root we will multiply the square roots value together. Let us understand this with a practical illustration. For example, multiply √4 × √16. The square root of 4 is 2 (√4 = 2) and the square root of 16 is 4 (√16 = 4). Now, we will multiply the value of the square root of 4 and 16, i.e., 2 × 4 = 8. Instead, we can apply the property of square roots, √a × √b = √ab.
What is the Formula for Calculating the Square Root of a Number?
The square root of any number can be expressed using the formula: √y = y½. In other words, if a number has 1/2 as its exponent, it means we need to find the square root of the number.
What is the Square and Square Root of a Number?
The square of a number is the product that we get on multiplying a number by itself. For example, 6 × 6 = 36. Here, 36 is the square of 6. The square root of a number is that factor of the number and when it is multiplied by itself the result is the original number. Now, if we want to find the square root of 36, that is, √36, we get the answer as, √36 = 6. Hence, we can see that the square and the square root of a number are inverse operations of each other.
Which Method is Used to Find the Square Root of Non-Perfect Square Numbers?
In Math, a non-perfect or an imperfect square number is considered as a number whose square root cannot be found as an integer or as a fraction of integers. The square root of a non-perfect square number can be calculated by using the long division method.
How to Find a Square Root on a Calculator?
To find the square root value of any number on a calculator, we simply need to type the number for which we want the square root and then insert the square root symbol √ in the calculator. For example, if we need to find the square root of 81, we should type 81 in the calculator and then press the symbol √ to get its square root. We will get √81 = 9.
☛ Check:
- Square Root Calculator
- Fraction Square Root Calculator
- Adding Square Roots Calculator
- Multiplying Square Roots Calculator
- Simplify Square Roots Calculator
What are the Applications of the Square Root Formula?
There are various applications of the square root formula:
- The square root formula is mainly used in algebra and geometry.
- It helps in finding the roots of a quadratic equation.
- It is widely used by engineers.
What does the Square of a Number mean?
The product that we get on multiplying a number by itself is the square of the number. For example, 5 × 5 = 25. Here, 25 is the square of 5 and this can also be written as 52 = 25.
How to Calculate the Square Root of a Negative Number?
Note that the square root of a negative number is not a real number. It is an imaginary number. For example, √(-4) = √(-1) × √4 = i (2) = 2i, where 'i' is known as "iota" and i2 = -1 (or) i = √(-1).
Why is the Square of a Negative Number Positive?
The square of a negative number is positive because when two negative numbers are multiplied it always results in a positive number. For example, (-4) × (-4) = 16.
visual curriculum