A day full of math games & activities. Find one near you.

Square Root of 256

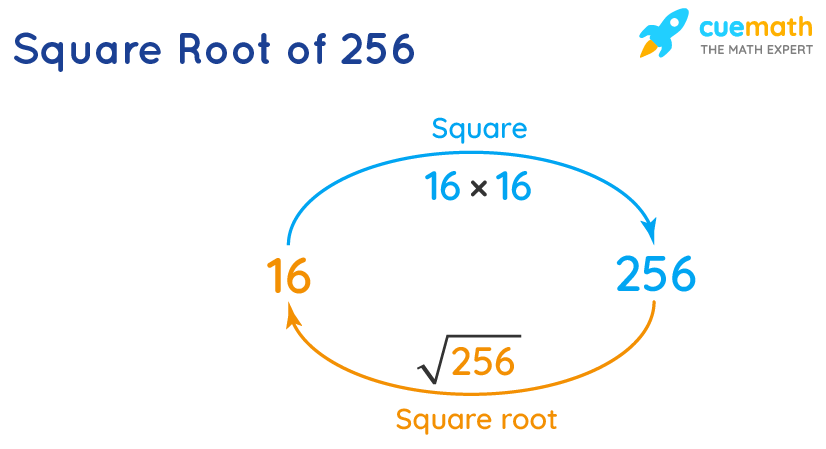
The square root of 256 is expressed as √256 in the radical form and as (256)^½ or (256)^0.5 in the exponent form. The square root of 256 is 16. It is the positive solution of the equation x² = 256. The number 256 is a perfect square.

Square Root of 256: 16
Square Root of 256 in exponential form: (256)^½ or (256)^0.5
Square Root of 256 in radical form: √256

1.	What Is the Square Root of 256?
2.	Is Square Root of 256 Rational or Irrational?
3.	How to Find the Square Root of 256?
4.	FAQs on Square Root of 256

What Is the Square Root of 256?

The square root of a number is the number which, when multiplied to itself, gives the original number.
For any two real numbers, a and b, a² = b and a = √b.
Let us understand the calculation of the square root of 256.
The square root of 256 is the number which, when multiplied with itself, will give the result as 256.
The square root of 256 is the inverse operation of squaring 16.
If 16² = 256, then √256 = 16

square root of 256 is the inverse of squaring 16

When we multiply two negative signs, we get a positive sign.
The multiplication of (-16) with itself will give the result as 256. Therefore, (-16) is also a square root of 256.
We will study the mathematical approach to calculate the square root of 256 in the following sections.

Is Square Root of 256 Rational or Irrational?

A rational number is defined as a number that can be expressed in the form of a quotient or division of two integers, i.e. p/q where q is not equal to 0.
The square root of 256 is either 16 or (-16).
13 and -13 can be expressed as 16/1 and -16/1.
Both the numbers can be represented in the form of a rational number.
Thus, the square root of 256 is a rational number.

How to Find the Square Root of 256?

The square root of 256 can be calculated using different methods such as: Prime Factorization and Long Division method.

Square Root of 256 by Prime factorization method

Step 1: Determine the prime factors using prime factorization. Prime factorization of 256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
Step 2. Group the prime factors obtained for 256 in pairs.
Step 3. Pick one factor from each pair and they can be written in the form: 256 = (2 × 2 × 2 × 2)²
Step 4. Thus, following the law of exponents, we get, √256 = √(16²) = 16^½
Thus we evaluate √256 = + 16 or -16

Square Root of 256 by Long Division Method

Step 1. Write 256 as shown in the figure. Start grouping the number in pairs from the right end. 56 is the first pair from the right.
Step 2: Find the largest number that when multiplied with itself will give 2 or a smaller number closest to 2. Here it is 1. Do the division and get the remainder.
Step 3: Bring down the next pair of numbers. Here it is 56. Multiply the quotient 1 by 2 and write it in the new divisor's place or the tens place. The number 2 will be placed in the tens place.
Step 4: Find the largest number that when kept at ones place with 2 at tens place multiplied with that same number gives a result 156 or a number closest to 156.
Step 5: Get the next quotient place as 6. Now we get our new divisor as 26 as 6 × 26 = 156. Complete the division and get the remainder. Here we get 0. Thus, the process of division completes here.

finding square root of 256 by division method

Explore square roots using illustrations and interactive examples.

Challenging Questions:

Roger was planning to cover a square table that has an area of √256 square inches. He found a cloth of area 18 square inches. How many inches does the cloth hang over the table on each side if the cloth is centered on the table?

Important Notes

The square root of 256 is expressed as √256 in the radical form and as 256^½ in the exponential form.

Square Root of 256 Solved Examples

Example 1: Chris orders a pizza whose surface area is 803.84 square inches. What is the radius of the pizza that Chris ordered?

Solution:

The total surface area of Chris's pizza = 803.84 square inches

The surface area of a circle = π × r²

3.141 × r² = 803.84

r² = 803.84 ÷ 3.141 = 256

r = √256

r = +16 or -16

Since the radius cannot be negative, we need to consider the positive value.

Therefore, the radius of the pizza that Chris ordered = 16 inches.
Example 2: Veronica makes as many bracelets in a day as the number of days that she has taken to make 256 of them. If she has made a total of 256 bracelets, how many bracelets has she made and how many days has she taken?

Solution:

Number of bracelets made = number of days taken.

Let the number of bracelets made per day = n

Let the number of days taken = n

n × n = 256

n² = 256

n = 16

Thus, she has taken 16 days to make 16 bracelets per day.
Example 3: If the area of an equilateral triangle is 256√3 in². Find the length of one of the sides of the triangle.

Solution:

Let 'a' be the length of one of the sides of the equilateral triangle.
⇒ Area of the equilateral triangle = (√3/4)a² = 256√3 in²
⇒ a = ±√1024 in
Since length can't be negative,
⇒ a = √1024 = 2 √256
We know that the square root of 256 is 16.
⇒ a = 32 in

go to slide go to slide go to slide

Breakdown tough concepts through simple visuals.

Math will no longer be a tough subject, especially when you understand the concepts through visualizations.

Book a Free Trial Class

FAQs on the Square Root of 256

What is the Value of the Square Root of 256?

The square root of 256 is 16.

Why is the Square Root of 256 a Rational Number?

Upon prime factorizing 256 i.e. 2⁸, we find that all the prime factors are in even power. This implies that the square root of 256 is a positive integer. Therefore, the square root of 256 is rational.

Is the number 256 a Perfect Square?

The prime factorization of 256 = 2⁸. Here, all the numbers are in the power of 2. This implies that the square root of 256 is a positive integer. Therefore, 256 is a perfect square.

What is the Square Root of -256?

The square root of -256 is an imaginary number. It can be written as √-256 = √-1 × √256 = i √256 = 16i
where i = √-1 and it is called the imaginary unit.

What is the Value of 4 square root 256?

The square root of 256 is 16. Therefore, 4 √256 = 4 × 16 = 64.

If the Square Root of 256 is 16. Find the Value of the Square Root of 2.56.

Let us represent √2.56 in p/q form i.e. √(256/100) = 16/10 = 1.6. Hence, the value of √2.56 = 1.6

Math worksheets and
visual curriculum