Complex Number

Complex numbers are helpful in finding the square root of negative numbers. The concept of complex numbers was first referred to in the 1st century by a greek mathematician, Hero of Alexandria when he tried to find the square root of a negative number. But he merely changed the negative into positive and simply took the numeric root value. Further, the real identity of a complex number was defined in the 16th century by Italian mathematician Gerolamo Cardano, in the process of finding the negative roots of cubic and quadratic polynomial expressions.

Complex numbers have applications in many scientific research, signal processing, electromagnetism, fluid dynamics, quantum mechanics, and vibration analysis. Here we can understand the definition, terminology, visualization of complex numbers, properties, and operations of complex numbers.

1.	What Are Complex Numbers?
2.	Graphing of Complex Numbers
3.	Properties of Complex Numbers
4.	Operations on Complex Numbers
5.	Algebraic Identities of Complex Numbers
6.	Solved Examples
7.	Practice Questions
8.	FAQs on Complex Numbers

What are Complex Numbers?

A complex number is the sum of a real number and an imaginary number. A complex number is of the form a + ib and is usually represented by z. Here both a and b are real numbers. The value 'a' is called the real part which is denoted by Re(z), and 'b' is called the imaginary part Im(z). Also, ib is called an imaginary number.

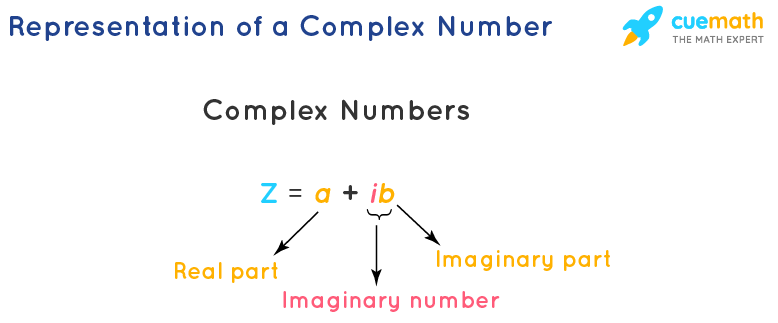
Representation of a Complex Number

Some of the examples of complex numbers are \(2+3i, -2-5i, \,\,\dfrac 1 2 + i\dfrac 3 2\), etc.

Power of i

The alphabet i is referred to as the iota and is helpful to represent the imaginary part of the complex number. Further the iota(i) is very helpful to find the square root of negative numbers. We have the value of i² = -1, and this is used to find the value of √-4 = √i²4 = +2i The value of i² = -1 is the fundamental aspect of a complex number. Let us try and understand more about the increasing powers of i.

i = √-1
i² = -1
i³ = i.i² = i(-1) = -i
i⁴ = (i²)² = (-1)² = 1
i⁴ⁿ = 1
i^{4n + 1} = i
i^{4n + 2} = -1
i^{4n + 3} = -i

Graphing of Complex Numbers

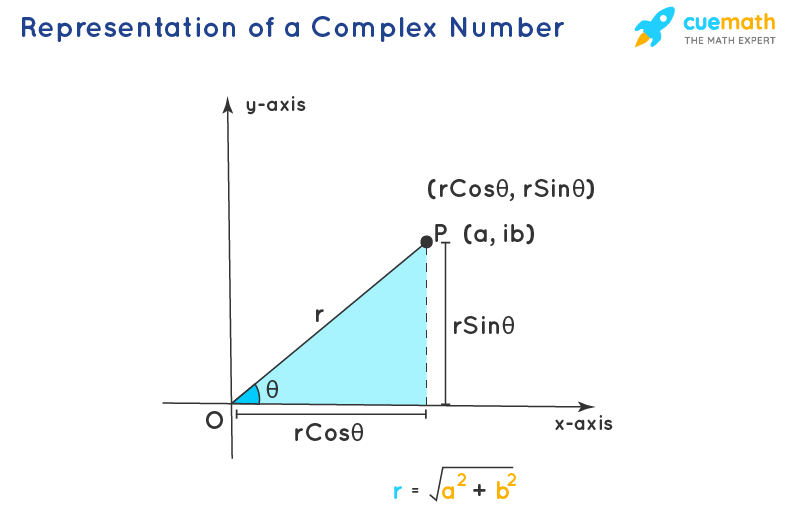
The complex number consists of a real part and an imaginary part, which can be considered as an ordered pair (Re(z), Im(z)) and can be represented as coordinates points in the euclidean plane. The euclidean plane with reference to complex numbers is called the complex plane or the Argand Plane, named after Jean-Robert Argand. The complex number z = a + ib is represented with the real part - a, with reference to the x-axis, and the imaginary part-ib, with reference to the y-axis. Let us try to understand the two important terms relating to the representation of complex numbers in the argand plane. The modulus and the argument of the complex number.

Modulus of the Complex Number

The distance of the complex number represented as a point in the argand plane (a, ib) is called the modulus of the complex number. This distance is a linear distance from the origin (0, 0) to the point (a, ib), and is measured as r = |\(\sqrt{a^2 + b^2}\)|. Further, this can be understood as derived from the Pythagoras theorem, where the modulus represents the hypotenuse, the real part is the base, and the imaginary part is the altitude of the right-angled triangle.

Argument of the Complex Number

The angle made by the line joining the geometric representation of the complex number and the origin, with the positive x-axis, in the anticlockwise direction is called the argument of the complex number. The argument of the complex number is the inverse of the tan of the imaginary part divided by the real part of the complex number. Argz (θ) = \(Tan^{-1}\frac{b}{a}\).

Representation of a Complex Number

Polar Representation of a Complex Number

With the modulus and argument of a complex number and the representation of the complex number in the argand plane, we have a new form of representation of the complex number, called the polar form of a complex number. The complex number z = a + ib, can be represented in polar form as z = r(Cosθ + iSinθ). Here r is the modulus (r = \sqrt{a^2 + n^2}\), and θ is the argument of the complex number(θ = \(Tan^{-1}\frac{b}{a}\)).

Properties of a Complex Number

The following properties of complex numbers are helpful to better understand complex numbers and also to perform the various arithmetic operations on complex numbers.

Conjugate of a Complex Number

The conjugate of the complex number is formed by taking the same real part of the complex number and changing the imaginary part of the complex number to its additive inverse. If the sum and product of two complex numbers are real numbers, then they are called conjugate complex numbers. For a complex number z = a + ib, its conjugate is \(\bar z\) = a - ib.

The sum of the complex number and its conjugate is \(z + \bar z\) = ( a + ib) + (a - ib) = 2a, and the product of these complex numbers \(z.\bar z\) = (a + ib) × (a - ib) = a² + b².

Reciprocal of a Complex Number

The reciprocal of complex numbers is helpful in the process of dividing one complex number with another complex number. The process of division of complex numbers is equal to the product of one complex number with the reciprocal of another complex number.. The reciprocal of the complex number z = a + ib is \(z^{-1} = \dfrac{ 1 }{ a + ib} = \dfrac{a - ib}{a^2 + b^2} = \dfrac{a}{a^2 + b^2} + \dfrac{i(-b)}{a^2 + b^2}\). This also shows that \(z \neq z^{-1}\).

Equality of Complex Numbers

The equality of complex numbers is similar to the equality of real numbers. Two complex numbers \(z_1 = a _1 + ib_1\) and \(z_2 = a_2 + ib_2 \) are said to be equal if the rel part of both the complex numbers are equal \(a_1 = a_2\), and the imaginary parts of both the complex numbers are equal \(b_1 = b_2 \). Also, the two complex numbers in the polar form are equal, if and only if they have the same magnitude and their argument (angle) differs by an integral multiple of 2π.

Ordering of Complex Numbers

The ordering of complex numbers is not possible. Real numbers and other related number systems can be ordered, but complex numbers cannot be ordered. The complex numbers do not have the structure of an ordered field, and there is no ordering of the complex numbers that are compatible with addition and multiplication. Also, the non-trivial sum of squares in an ordered field is a number \(\neq 0\), but in a complex number, the non-trivial sum of squares is equal to i² + 1² = 0. The complex numbers can be measured and represented in a two-dimensional argrand plane by their magnitude, which is its distance from the origin.

Euler's Formula: As per Euler's formula for any real value θ we have e^iθ = Cosθ + iSinθ, and it represents the complex number in the coordinate plane where Cosθ is the real part and is represented with respect to the x-axis, Sinθ is the imaginary part that is represented with respect to the y-axis, θ is the angle made with respect to the x-axis and the imaginary line, which is connecting the origin and the complex number. As per Euler's formula and for the functional representation of x and y we have e^{x + iy} = e^x(cosy + isiny) = e^xcosy + ie^xSiny. This decomposes the exponential function into its real and imaginary parts.

Operations on Complex Numbers

The various operations of addition, subtraction, multiplication, division of natural numbers can also be performed for complex numbers also. The details of the various arithmetic operations of complex numbers are as follows.

Addition of Complex Numbers

Th addition of complex numbers is similar to the addition of natural numbers. Here in complex numbers, the real part is added to the real part and the imaginary part is added to the imaginary part. For two complex numbers of the form \(z_1 = a + id\) and \(z_2 = c + id\), the sum of complex numbers \(z_1 + z_2 = (a + c) + i(b + d)\). The complex numbers follow all the following properties of addition.

Closure Law: The sum of two complex numbers is also a complex number. For two complex numbers \(z_1\) and \(z_2\), the sum of \(z_1 + z_2\) is also a complex number.
Commutative Law: For two complex numbers \(z_1\), \(z_2\) we have \(z_1 + z_2 = z_2 + z_1\).
Associative Law: For the given three complex numbers \(z_1, z_2, z_3\) we have \(z_1 + (z_2 + z_3) = (z_1 + z_2)+z_3 \).
Additive Identity: For a complex number z = a + ib, there exists 0 = 0 + i0, such that z + 0 = 0 + z = 0.
Additive Inverse: For the complex number z = a + ib, there exists a complex number -z = -a -ib such that z + (-z) = (-z) + z = 0. Here -z is the additive inverse.

Subtraction of Complex Numbers

The subtraction of complex numbers follows a similar process of subtraction of natural numbers. Here for any two complex numbers, the subtraction is separately performed across the real part and then the subtraction is performed across the imaginary part. For the complex numbers \(z_1\) = a + ib, \(z_2 = c + id \), we have \(z_1 - z_2 \) = (a - c) + i(b - d)

Multiplication of Complex Numbers

The multiplication of complex numbers is slightly different from the multiplication of natural numbers. Here we need to use the formula of \(i^2 = -1\). For the two complex numbers \(z_1\) = a + ib, \(z_2\) = c + id, the product is \(z_1.z_2\) = (ca - bd) + i(ad + bc).

The multiplication of complex numbers is polar form is slightly different from the above mentioned form of multiplication. Here the absolute values of the two complex numbers are multiplied and their arguments are added to obtain the product of the complex numbers. For the complex numbers \(z_1 = r_1(Cos\theta_1 + iSin\theta_1)\), and z₂ = \(z_2 = r_1(Cos\theta_2 + iSin\theta_2)\), the product of the complex numbers is \(z_1.z_2 = r_1.r_2(Cos(\theta_1 + \theta_2) + iSin(\theta_1 + \theta_2))\).

Division of Complex Numbers

The division of complex numbers makes use of the formula of reciprocal of a complex number. For the two complex numbers \(z_1\) = a + ib, \(z_2\) = c + id, we have the division as \(\dfrac{z_1}{z_2 } = (a + ib) × \dfrac{1}{(c + id) }= (a + ib) × \dfrac{(c - id)}{(c^2 + d^2)}\).

Algebraic Identities of Complex Numbers

All the algebraic identities apply equally for complex numbers.The addition and subtraction of complex numbers and with exponents of 2 or 3 can be easily solved using algebraic identities of complex numbers.

\((z_1 + z_2)^2 = z_1^2 + 2z_1z_2 + z_2^2\)
\((z_1 - z_2)^2 = z_1^2 - 2z_1z_2 + z_2^2\)
\((z_1 + z_2)^3 = z_1^3 + 3z_1^2z_2 +3z_1z_2^2 + z_2^3\)
\((z_1 - z_2)^3 = z_1^3 - 3z_1^2z_2 +3z_1z_2^2 - z_2^3\)
\((z_1 + z_2)(z_1 - z_2) = z_1^2 - z_2^2\)
\((z_1 + z_2+z_3)^2 = z_1^2 + z_2^2+z_3^2 + 2z_1z_2 +2z_2z_3 +2z_3z_1\)

Related Topics:

Complex Numbers Tips and Tricks:

All real numbers are complex numbers but all complex numbers don't need to be real numbers.
All imaginary numbers are complex numbers but all complex numbers don't need to be imaginary numbers.
The conjugate of a complex number \(z=a+ib\) is \(\overline{z} = a-ib\).
The magnitude of a complex number \(z=a+ib\) is \(|z|=\sqrt{a^2+b^2}\).

Example 1: Can we help Sophia express the roots of the quadratic equation \(x^2+x+1=0\) as complex numbers?

Solution:

Comparing the given equation with \(ax^2+bx+c=0\), \[a=1\\[0.2cm]b=1\\[0.2cm]c=1\]

(This equation is as same as the one we saw in the beginning of this page).

Substitute these values in the quadratic formula:

\[\begin{align} x&= \dfrac{-b \pm \sqrt{b^2-4ac}}{2a}\\[0.2cm]
&=\frac{-1 \pm \sqrt{1^{2}-4(1)(1)}}{2(1)} \\[0.2cm]
&=\frac{-1 \pm \sqrt{-3}}{2}\\[0.2cm]
\text{Here, } &\sqrt{-3} = \sqrt{-1} \times \sqrt{3} = i \sqrt{3}\\[0.2cm]
x&= \frac{-1 \pm i\sqrt{3}}{2}\\[0.2cm]
\end{align} \]

Thus the roots of the given quadratic equation are: \(\frac{-1}{2}+ i\frac{\sqrt{3}}{2};\,\,\, \frac{-1}{2}- i\frac{\sqrt{3}}{2}\)
Example 2: Express the sum, difference, product, and quotient of the following complex numbers as a complex number.

\[\begin{align} z_1&=-2+i\\[0.2cm]z_2&= 1-2i \end{align} \]

Solution:

Sum:

\[ \begin{align} z_1+z_2&= (-2+i)+(1-2i)\\[0.2cm] &=(-2+1)+ (i-2i)\\[0.2cm] &= -1-i \end{align}\]

Difference:

\[ \begin{align} z_1-z_2&= (-2+i)-(1-2i)\\[0.2cm] &=(-2-1)+ (i+2i)\\[0.2cm] &= -3+3i \end{align}\]

Product:

\[ \begin{align} z_1\cdot z_2&= (-2+i)(1-2i)\\[0.2cm] &=-2+4i+i-2i^2\\[0.2cm] &=-2+4i+i+2 \,\,\, [\because i^2=-1]\\[0.2cm] &=5i \end{align}\]

Quotient:

\[\begin{align} \dfrac{z_1}{z_2}&= \dfrac{-2+i}{1-2i}\\[0.2cm] &= \dfrac{-2+i}{1-2i} \cdot \dfrac{1+2i}{1+2i}\\[0.2cm] &= \dfrac{-2-4i+i+2i^2}{1-4i^2}\\[0.2cm] &= \dfrac{-2-4i+i-2}{1+4}\,\,\, [\because i^2=-1]\\[0.2cm] &= \dfrac{-4-3i}{5}\\[0.2cm] &=- \dfrac{4}{5}- i \dfrac{3}{5}\end{align}\]

Therefore, we have:

Sum = -1 - i
Difference = -3 + 3i
Product = 5i
Division = -4/5 - 3i/5

go to slide go to slide

Breakdown tough concepts through simple visuals.

Math will no longer be a tough subject, especially when you understand the concepts through visualizations.

Book a Free Trial Class

go to slide go to slide

FAQs on Complex Numbers

What are Complex Numbers in Math?

A complex number is a combination of real values and imaginary values. It is denoted by z = a + ib, where a, b are real numbers and i is an imaginary number. i = \(\sqrt{-1}\) and no real value satisfies the equation i² = -1, therefore, I is called the imaginary number.

What are Complex Numbers Used for?

The complex number is used to easily find the square root of a negative number. Here we use the value of i² = -1 to represent the negative sign of a number, which is helpful to easily find the square root. Here we have √-4 = √i²4 = + 2i. Further to find the negative roots of the quadratic equation, we used complex numbers.

What is Modulus in Complex Numbers?

The modulus of a complex number z = a + ib is the distance of the complex number in the argand plane, from the origin. It is represented by |z| and is equal to r = \(\sqrt{a^2 + b^2}\). If a complex number is considered as a vector representation in the argand plane, then the module of the complex number is the magnitude of that vector.

What is Argument in Complex Numbers?

The argument of a complex number is the angle made by the line joining the origin to the geometric representation of the complex number, with the positive x-axis in the anticlockwise direction. The argument of the complex number is the inverse of the tan of the imaginary part divided by the real part of the complex number. Argz (θ) = \(Tan^{-1}\frac{b}{a}\).

How to Perform Multiplication of Complex Numbers?

The multiplication of complex numbers is slightly different from the multiplication of natural numbers. Here we need to use the formula of i² = -1. For the two complex numbers \(z_1\) = a + ib, \(z_2\) = c + id, the product is \(z_1.z_2\) = (ca - bd) + i(ad + bc).

What is Polar Form in Complex Numbers?

The polar form of a complex number is another form of representing and identifying a complex number in the argand plane. The polar form makes the use of the modulus and argument of a complex number, to represent the complex number. The complex number z = a + ib, can be represented in polar form as z = r(Cosθ + iSinθ). Here r is the modulus (r = \sqrt{a^2 + n^2}\), and θ is the argument of the complex number(θ = \(Tan^{-1}\frac{b}{a}\)).

What Are Real and Complex Numbers?

Complex numbers are a part of real numbers. Certain real numbers with a negative sign are difficult to compute and we represent the negative sign with an iota 'i', and this representation of numbers along with 'i' is called a complex number. Further complex numbers are useful to find the square root of a negative number, and also to find the negative roots of a quadratic or polynomial expression.

How To Divide Complex Numbers?

How to Graph Complex Numbers?

The complex number of the form z = a + ib can be represented in the argand plane. The complex number z = a + ib can be presented as the coordinates of a point as (Re(z), Im(z)) = (a, ib). Here the real part is presented with reference to the x-axis, and the imaginary part is presented with reference to the y-axis.

How to Convert Complex Numbers to Polar Form?

The complex number can be easily converted into a polar form. The complex number z = a + ib has a modulus (r = \sqrt{a^2 + n^2}\), and an argument (θ = \(Tan^{-1}\frac{b}{a}\)). With the help of modulus and argument the polar form of the complex number is written as z = r(Cosθ + iSinθ).

How to Write Complex Numbers in Standard Form?

The standard form of writing a complex number is z = a + ib. The standard form of the complex number has two parts, the real part, and the imaginary part. In the complex number z = a + ib, a is the real part and ib is the imaginary part.

How Complex Numbers were Invented?

The inverse of a complex numbers is helpful in the process of dividing one complex number with another complex number. The process of division of complex numbers is equal to the product of one complex number with the inverse of another complex number.. The inverse of the complex number z = a + ib is \(z^{-1} = \dfrac{ 1 }{ a + ib} = \dfrac{a - ib}{a^2 + b^2} = \dfrac{a}{a^2 + b^2} + \dfrac{i(-b)}{a^2 + b^2}\). This also shows that \(z \neq z^{-1}\).

Download FREE Study Materials

Download Complex Numbers Worksheets

Math worksheets and
visual curriculum