Additive Inverse
Additive inverse is the number that is added to a given number to make the sum zero. For example, if we take the number 3 and add -3 to it, the result is zero. Hence, the additive inverse of 3 is -3. We come across such situations in our daily life where we nullify the value of a quantity by taking its additive inverse. Let us learn the additive inverse property of real and complex numbers in this article.
What is Additive Inverse?
The additive inverse of a number is its opposite number. If a number is added to its additive inverse, the sum of both the numbers becomes zero. The simple rule is to change the positive number to a negative number and vice versa. We know that, 7+ (-7) =0. Thus -7 is the additive inverse of 7 and 7 is the additive inverse of -7.
Additive Inverse Property
When the sum of two real numbers is zero, then each real number is said to be the additive inverse of the other. So, we have R + (-R) = 0, where R is a real number. R and -R are the additive inverses of each other. For example: 3/4 + (-3/4) = 0. Here 3/4 is the additive inverse of -3/4 and vice-versa. This is an example of the additive inverse of a fraction.
Let’s say you have a bucket of water at room temperature. You add a liter of hot water to it which makes the overall temperature of the bucket rise by a certain amount. Now, add another liter of cold water to it. The contrasting temperatures of water added to the bucket will cancel out each other, and the result will be a bucket of water at room temperature. The same rule applies while finding the additive inverse of a number. The additive inverse property holds good for both real numbers and complex numbers.
Additive Inverse of Real Numbers
The given number can be a whole number, a natural number, an integer, a fraction, a decimal, or any real number. The additive inverse of real numbers is just the negative of the given number.
| Example | Given Number | Additive Inverse |
|---|---|---|
| Natural Numbers | 12 | -12 |
| Whole Numbers | 6 | -6 |
| Integers | -12 | 12 |
| Fractions | -4/5 | 4/5 |
| Decimals | 2.5 | -2.5 |
Additive Inverse of Complex Numbers
The algebraic property of complex numbers states the existence of additive inverse. Given any complex number z ∈ C, there is a unique complex number, denoted by -z, such that z + (-z) = 0. Moreover, if z = (x,y) with x,y ∈ R, then -z = (-x,-y).
Let Z = x + iy be the given complex number. Then its inverse is -Z = -x - iy. For example, the additive inverse of - i - 1 = - (- i - 1) = i + 1.
Additive Inverse of a Fraction
The additive inverse of a fraction a/b is -a/b, and vice-versa. It is because a/b + (-a/b) = 0. The additive inverse of a positive fraction is the same fraction with the negative sign, while for a negative fraction, its additive inverse is the same fraction without the negative sign.
Additive Inverse Formula
The general formula for the additive inverse of a number can be given in the form of the number itself. Any number when added to its negative will cancel out each other and give the overall sum as zero. We need to find the negative of the given number N. In other words, we need to find -1 × (N). Hence, we can say that:
Additive Inverse of N = -1 × (N)
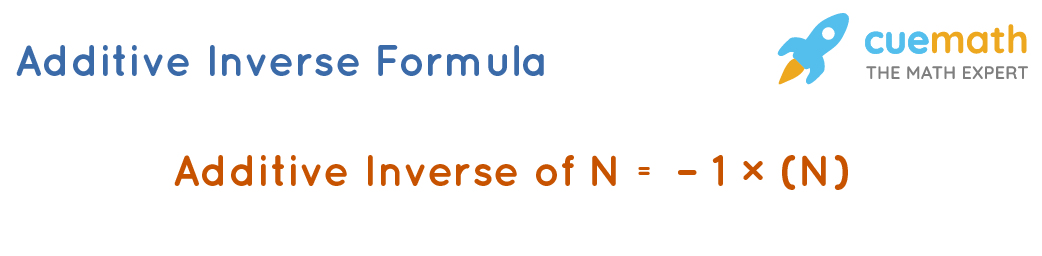
Additive Inverse and Multiplicative Inverse
There are two properties of numbers: multiplicative inverse and additive inverse property related to the multiplication and addition operation respectively. For a number x, - x is the additive inverse and 1/x is the multiplicative inverse. Let us understand the difference between additive inverse and multiplicative inverse with the help of the following table:
| Additive Inverse | Multiplicative Inverse |
|---|---|
| To find the additive inverse, we change the sign of the number. | To find the multiplicative inverse, we take the reciprocal of the number. |
| It is added to the original number to get 0. | It is multiplied by the given number to get 1. |
| Equation: a + (-a) = 0 | Equation: a × 1/a = 1 |
Additive Inverse in Algebraic Expressions
The property of additive inverse can be extended to algebraic expressions. Following the same rule as stated above, the additive inverse of an algebraic expression is one that makes the sum of all the terms zero. Note: The additive inverse of the expression is -(expression). The additive inverse of x2 + 1 is - (x2 + 1) = -x2 - 1.
For example, the additive inverse of 2x + 3y is -2x - 3y, making the sum of all the elements zero.
☛ Related Articles:
FAQs on Additive Inverse
What is the Additive Inverse?
Additive inverse is what you add to a number to make the sum zero. For example, the additive inverse of 4 is -4 because their sum is zero. When two numbers are added together to get 0, then we say both the numbers are additive inverses of each other.
How do you Find the Additive Inverse of a Given Number?
In order to find the additive inverse of a given number, we just change the sign of the given number to get its additive inverse. For example, the additive inverse of 8 is -8 and the additive inverse of -35 is 35.
What is the Additive Inverse Formula?
The additive inverse formula is -1 × R, where R is any real number. This formula can be applied to any number to get its additive inverse. For example, if we need to get the additive inverse of 7, let us substitute 7 in the formula, -1 × R = -1 × 7 = -7. Therefore, the additive inverse of 7 is -7.
What is the Additive Inverse of Zero?
Since zero does not have a positive or negative sign associated with it, the additive inverse of zero is zero.
Is Additive Inverse Same as Additive Identity?
No, additive inverse and the additive identity property are not the same. The additive inverse of a given number is obtained by just reversing its sign. This means when the given number and its additive inverse are added we get 0. For example, the additive inverse of 4 is -4 → ( 4 + (- 4) = 0). Whereas, the additive identity of any given number is 0, because when we add any number to zero, it results in the number itself. For example, the additive identity of 4 is 0 → (4 + 0 = 4).
What is the Difference between Additive Inverse and Multiplicative Inverse?
Additive inverse is what we add to a number to make the sum zero, whereas, the multiplicative inverse is the reciprocal of the given number, which when multiplied together, gives the product as 1.
Does 0 have an Additive Inverse?
Yes, since zero does not have a positive or negative sign associated with it, the additive inverse of 0 is 0.
What is the Additive Inverse of 7?
The additive inverse of 7 is -7. This can be verified as: 7 + (-7) = 0.
What is the Additive Inverse of 12?
The additive inverse of 12 is -12. This can be verified by: 12 + (-12) = 0.
What is the Additive Inverse of 2/3?
The additive inverse of 2/3 is -2/3. This can be verified by: 2/3 + (-2/3) = 0.