Algebraic Expressions
Algebraic expressions are the mathematical statement that we get when operations such as addition, subtraction, multiplication, division, etc. are operated upon on variables and constants. For example, let us assume that James and Natalie were playing with matchsticks and thought of forming number patterns using them. James took four matchsticks and formed the number 4. Natalie added three more matchsticks to form a pattern with two 4's. They realized that they can keep on adding 3 matchsticks in each round to make one extra "four". From this, they concluded that they need 4+ 3(n-1) sticks, in general, to make a pattern with n number of 4's. Here, 4+ 3(n-1) is called an algebraic expression.
Let us learn more about algebraic expressions along with their types and operations on them.
What are Algebraic Expressions?
An algebraic expression (or) a variable expression is a combination of terms by the operations such as addition, subtraction, multiplication, division, etc. For example, let us have a look at the expression 5x + 7. Thus, we can say that 5x + 7 is an example of an algebraic expression. Here are more examples:
- 5x + 4y + 10
- 2x2y - 3xy2
- (-a + 4b)2 + 6ab
Variables, Constants, Terms, and Coefficients
There are different components of an algebraic expression. Let us have a look at the image given below in order to understand the concept of Variables, Constants, Terms, and Coefficients of any algebraic expression.
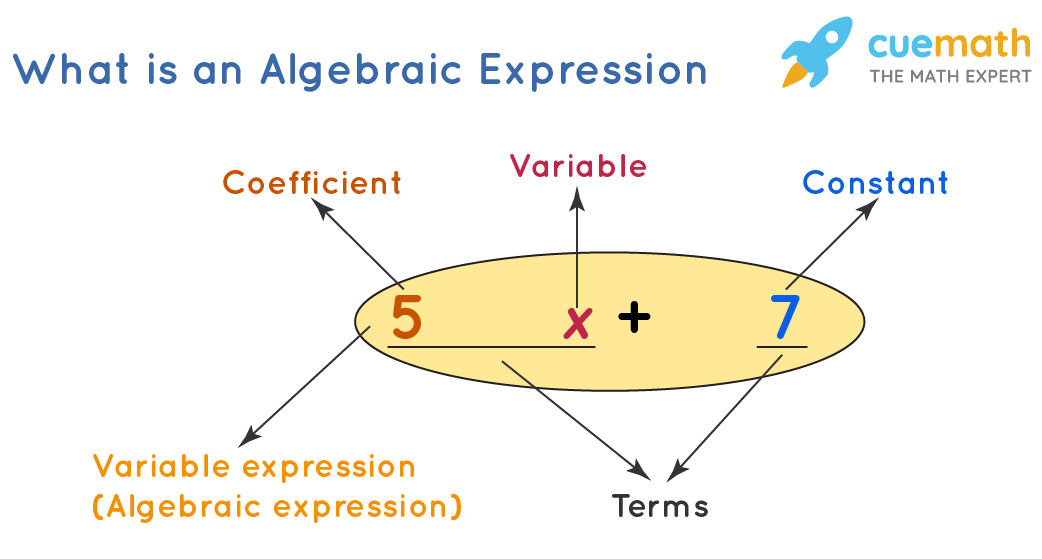
In mathematics,
- a symbol that doesn't have a fixed value is called a variable. It can take any value. In the above example that involved matchsticks, n is a variable and in this case, it can take the values 1,2,3,... Some examples of variables in Math are a,b, x, y, z, m, etc.
- On the other hand, a symbol that has a fixed numerical value is called a constant. All numbers are constants. Some examples of constants are 3, 6, -(1/2), √5, etc.
- A term is a variable alone (or) a constant alone (or) it can be a combination of variables and constants by the operation of multiplication or division. Some examples of terms are 3x2, -(2y/3), √(5x), etc.
- Here, the numbers that are multiplying the variables are 3, -2/3, and 5. These numbers are called coefficients.
Simplifying Algebraic Expressions
To simplify an algebraic expression, we just combine the like terms. Hence, the like variables will be combined together. Now, out of the like variables, the same powers will be combined together. For example, let us take an algebraic expression and try to reduce it to its lowest form in order to understand the concept better. Let our expression be:
x3 + 3x2 − 2x3 + 2x − x2 + 3 − x
= (x3 − 2x3) + (3x2 − x2) + (2x − x) + 3
= −x3 + 2x2 + x + 3
Hence, the algebraic expression x3 + 3x2 − 2x3 + 2x − x2 + 3 − x simplifies to −x3 + 2x2 + x + 3.
Adding Algebraic Expressions
Here are some examples for adding algebraic expressions:
- (x2 + 2x + 3) + (2x2 - 3x) = (x2 + 2x2) + (2x + (-3x)) + 3 = 3x2 - x + 3
- (1.5ab + 3) + (2.5ab - 2) = (1.5ab + 2.5ab) + (3 + (-2)) = 4ab + 1
Subtracting Algebraic Expressions
To subtract two algebraic expressions, we add the additive inverse of the second expression to the first expression. Here are some examples for subtracting algebraic expressions:
- (3x2 - 5x) - (x2 - 2x + 2) = (3x2 - 5x) + (-x2 + 2x - 2) = (3x2 - x2) + (-5x + 2x) - 2 = 2x2 - 3x - 2
- (3ab + 4) - (2ab - 4) = (3ab + 4) + (-2ab + 4) = (3ab - 2ab) + (4 + 4) = ab + 8
Multiplying Algebraic Expressions
To multiply two algebraic expressions, we multiply every term of the first expression with every term of the second expression and combine all the products. Here are some examples of multiplying algebraic expressions.
- ab (2ab + 3) = 2a2b2 + 3ab
- (x + 1) (x + 2) = x2 + x + 2x + 2 = x2 + 3x + 2
Dividing Algebraic Expressions
To divide two algebraic expressions, we factor the numerator and the denominator, cancel the possible terms, and simplify the rest. Here are some examples of dividing algebraic expressions.
- 2x2 / (2x2 + 4x) = (2x2) / [2x (x + 2)] = x / (x + 2)
- (x2 + 5x + 4) / (x + 1) = [ (x + 4) (x + 1) ] / (x + 1) = x + 4
Algebraic Expression Formulas
Algebraic formulas are the derived short formulas that help us in solving the equations easily. They are just a rearrangement of the given terms in order to create a better expression that is easy to memorize. Find below a list of some of the basic formulas that are being used widely. Have a look at this page in order to understand the algebraic formulas better.
- (a + b)2 = a2 + 2ab + b2
- (a - b)2 = a2 - 2ab + b2
- (a + b)(a - b) = a2 - b2
- (x + a)(x + b) = x2 + x(a + b) + ab
- (a + b)3 = a3 + 3a2b + 3ab2 + b3
- (a - b)3 = a3 - 3a2b + 3ab2 - b3
- a3 + b3 = (a + b) (a2 - ab + b2)
Types of Algebraic Expressions
The types of algebraic expressions are based on the variables found in that particular expression, the number of the terms of that expression, and the values of the exponents of the variables in each expression. Given below is a table that divides the algebraic expressions into five different categories. Let us have a look at the table.
| Type of Algebraic Expression | Meaning | Examples |
|---|---|---|
|
An expression with only one term where the exponents of all the variables are non-negative integers |
3xy | |
|
An expression with two monomials |
(3/4)x - 2y2 | |
|
An expression with three monomials |
3x-2y+ z | |
|
An expression with one or more monomials |
-(2/3)x3 + 7x2 + 3x + 5 | |
|
Multinomial |
An expression with one or more terms (the exponents of variables can be either positive or negative) |
4x-1 +2y+3z |
☛Related Topics:
FAQs on Algebraic Expressions
How do you Describe an Algebraic Expression?
An algebraic expression is a variable expression described using its terms, and operations on the terms. For example, x + 3 can be described as "3 more than x". While a + b - 7 can be described as "7 less than the sum of a and b".
How Many Terms are There in an Algebraic Expression?
A term is a variable alone (or) a constant alone (or) it can be a combination of variables and constants by the operation of multiplication or division. We apply this definition to identify the terms in an algebraic expression. After we identify the terms, we can just count them.
Why are Algebraic Expressions Useful?
The algebraic expressions use variables (which take multiple multiples) in order to describe a real-life scenario. Instead of saying "The cost of 3 pens and 4 pencils", it is simple to say 3x+4y where x and y are the costs of each pen and pencil respectively. Also, writing a real-life scenario as an expression helps to perform mathematical calculations.
How do you Identify an Algebraic Expression?
An algebraic expression is a combination of variables and constants. However, no equalities should be present in it. Otherwise, it will become an algebraic equation.
How to Simplify an Algebraic Expression?
To simplify an algebraic expression, we just combine the like terms and solve further to get a simplified form of the expression.
Is 7 an Algebraic Expression?
Yes, 7 is an algebraic expression, because it can be considered as a monomial.
What are Algebraic Expression and Equation?
An algebraic expression is any number, variable, or different operations combined together, while an equation is two different algebraic expressions combined together with an equal sign.