Algebra 1
Algebra 1 or elementary algebra includes the traditional topics studied in the modern elementary algebra course. Basic arithmetic operations comprise numbers along with mathematical operations such as +, -, x, ÷. While, algebra involves variables like x, y, z, and mathematical operations like addition, subtraction, multiplication, and division to form a meaningful mathematical expression.
Algebra helps in the representation of different situations or problems as mathematical expressions. The concepts that come under algebra 1 or elementary algebra include variables, evaluating expressions and equations, properties of equalities and inequalities, solving the algebraic equations and linear equations which have one or two variables, and so on.
| 1. | What is Algebra 1? |
| 2. | Algebra 1 Topics |
| 3. | Laws of Algebra 1 |
| 4. | Algebra 1 Formulas |
| 5. | Difference between Algebra 1 and Algebra 2 |
| 6. | Algebra 1: Tips and Tricks |
| 7. | FAQs on Algebra 1 |
What is Algebra 1?
Algebra 1 consists of the general/basic concepts of algebra. It introduces evaluating equations and inequalities, real numbers, and their properties, which include additive and multiplicative identities, inverse operations, and the distributive and commutative properties. In algebra 1, we will also be introduced to the concept of polynomials, and will also incorporate a bit of geometry to calculate the area, volume, and perimeters of shapes using algebraic expressions instead of numbers.
Algebra 1 or elementary algebra deals with solving the algebraic expressions for a viable answer. In algebra 1, simple variables like x, y, are represented in the form of an equation. Based on the degree of the variable the equations can be categorized into different types, namely linear equations, quadratic equations, cubic equations, and so on. Linear equations are of the forms of ax + b = c, ax + by + c = 0, ax + by + cz + d = 0. Elementary algebra based on the degree of the variables, branches out into quadratic equations and polynomials. A general form of representation of a quadratic equation is ax2 + bx + c = 0, and for a polynomial equation, it is axn + bxn-1+ cxn-2+ .....k = 0.
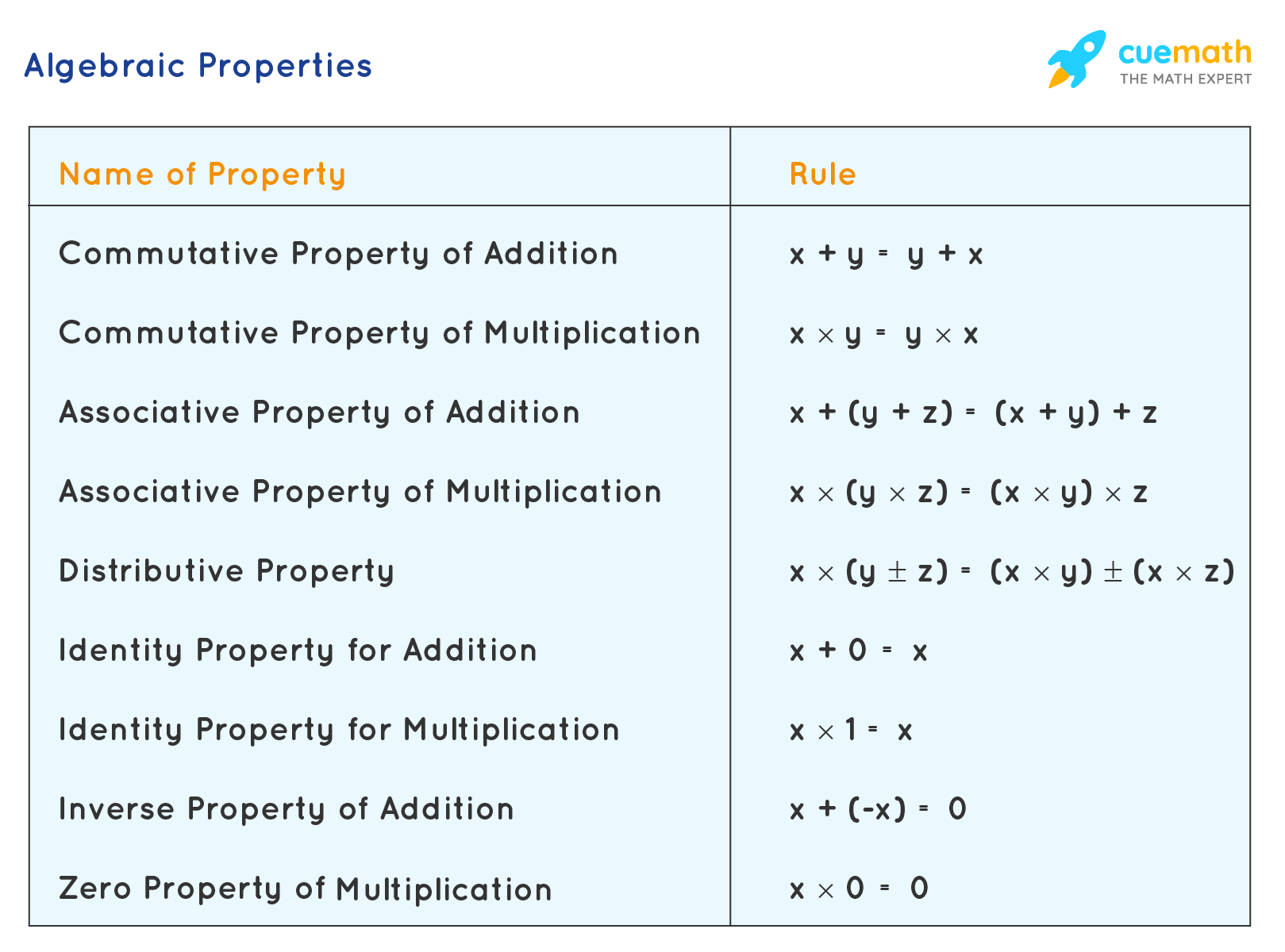
The rules for different properties under algebra 1 can be understood better as shown below,
Algebra 1 Topics
Algebra is divided into numerous topics to help for a detailed study. Algebra 1 is divided into 12 chapters and each chapter is divided into several lessons. These 12 chapters in Algebra 1 are given as:
Chapter 1: Real Numbers and Their Operations
Chapter 2: Linear Equations and Inequalities
Chapter 3: Introduction to Functions
- What Are Functions?
- Polynomial Functions
- Visualizing Functions Through Graphs
- Arithmetic and Geometric Progressions
Chapter 4: Graphing Lines
Chapter 5: Solving Linear Systems
- Solving Linear Systems by Substitution
- Solving Linear Systems by Cross Multiplication
- System of Equations Solver
- Solutions of a Linear Equation
Chapter 6: Polynomials and Their Operations
Chapter 7: Factoring and Solving by Factorization
- What is a Factor?
- Factoring Methods
- Factorization of Algebraic Expressions
- Factorization of Quadratic Equations
Chapter 8: Exponents And Exponential Functions
Chapter 9: Rational Expressions and Equations
Chapter 10: Radical Expressions and Equations
Chapter 11: Solving Quadratic Equations and Graphing Parabolas
- Square and Square Roots
- Quadratic Formula
- Graphing a Quadratic Function
- Complex Numbers and Complex Solutions
Chapter 12: Data Analysis And Probability
Laws of Algebra 1
The basic laws of algebra are the associative, commutative, and distributive laws that are presented in the table below:
| Property Name | Definition | Example |
|---|---|---|
| Commutative Law For Addition |
(a + b) = (b + a). According to the commutative property, swapping the positions of operands in an operation does not affect the result. |
If (4x + 3x) = 7x, then (3x + 4x) = 7x |
| Commutative Law For Multiplication |
(a × b) = (b × a). According to the commutative property, swapping the positions of operands in an operation does not affect the result. |
If (2x × 4) = 8x, then (4 × 2x) = 8x |
| Associative Law For Addition |
a + (b + c) = (a + b) + c. This grouping of addends does not affect the sum. |
If 3y + (4y + 5y) = (3y + 9y) = 12y, then (3y + 4y) + 5y = 7y + 5y = 12y |
| Associative Law For Multiplication |
a × (b × c) = b × (a × c). This grouping of factors does not affect the product. |
If 3a × (2b × 5c) = 3a × (10bc) = 30abc, then, (3a × 2b) × 5c = 6ab × 5ac = 30abc |
| Distributive Law For Addition |
a × (b + c) = (a × b) + (a × c). Adding two numbers and then multiplying them with a third gives the same result as multiplying the two numbers individually to the third and thereafter adding the obtained result. |
If 4x × (3y + 2y) = (4x × 5y) = 20xy, then (4x × 3y) + (4x × 2y) = 12xy + 8xy = 20xy |
| a × (b - c) = (a × b) - (a × c). Subtracting two numbers and then multiplying them with a third gives the same result as multiplying the two numbers individually to the third and thereafter subtracting the obtained result. | If 4x × (3y - 2y) = (4x × y) = 4xy, then (4x × 3y) - (4x × 2y) = 12xy - 8xy = 4xy |
Algebra 1 Formulas
Here are the list of formulas that are very useful in solving Algebra 1 problems.
- Algebraic identities:
(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 - 2ab + b2
(a + b)(a - b) = a2 - b2
(x + a)(x + b) = x2 + x(a + b) + ab
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a - b)3 = a3 - 3a2b + 3ab2 - b3
a3 + b3 = (a + b)(a2 - ab + b2)
a3 - b3 = (a - b)(a2 + ab + b2)
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca - Properties of Exponents:
am. an = am + n
am/an = am - n
(am)n = an
(ab)m = am. bm
a0 = 1
a-m = 1/am - Linear Equations Formulas:
General form: ax + by = c
Slope Intercept Form: y = mx + b
Two-Point Form: y−y1=m(x−x1)
Intercept Form: x/a + y/b = 1
Vertical Line through (p, q): x = p
Horizontal Line through (p, q): y = q - Quadratic Equations Formulas:
The standard form of quadratic equation is ax2 + bx + c = 0
Vertex form of quadratic equation is a (x - h)2 + k = 0
Quadratic Formula: The roots of a quadratic equation ax2 + bx + c = 0 are given by x = [-b ± √(b² - 4ac)]/2a. - Arithmetic Sequence Formulas:
nth term, an=a1+(n−1)d
Sum = n/2 [2a + (n - 1) d] (OR) n/2 [a1 + an] - Geometric Sequence Formulas:
The nth term of the geometric sequence is, an = a · rn - 1.
Sum of n terms, Sn = a (rn - 1) / (r - 1)
Sum of infinite terms, S = a / (1 - r) - Average rate of change formula: [f(b) - f(a)] / (b - a)
- Compound Interest Formula: A = P (1 + r / n)n t
- Statistics Formulas:
Mean = (Sum of Observations) ÷ (Total Numbers of Observations)
Mean of Grouped Data = Σfi/N
Median when 'n' is odd: [(n + 1)/2]th term; Median when 'n' is even: [(n/2)th term + ((n/2) + 1)th term]/2
Range = Maximum - Minimum
Interquartile Range = Upper quartile - Lower quartile
Difference Between Algebra 1 and Algebra 2
Algebra 1 and Algebra 2 can be distinguished based on the complexity and use of algebraic expressions. The following table explains the important differences between algebra 1 and algebra 2.
| Algebra 1 | Algebra 2 |
|---|---|
| Algebra 1 introduces you to the general concepts of algebra. You learn about variables, functions, and the most important concept in all of algebra. | Algebra 2 is much more advanced. It's also much more miscellaneous: you learn about everything from logarithms and complex numbers to implicit functions and conics to the fundamental theorem of algebra. |
| Algebra 1 helps students to have the basic command in algebra topics. | Algebra 2 increases complexity and understanding of the topics learned in algebra 1. |
| In this, students learn how to manipulate exponents or polynomials and write them in simpler forms, etc. | In this, students learn to apply the skills thus obtained in algebra 1 and also learn more difficult techniques. |
| Algebra 1 is concentrated on solving equations and inequalities | Algebra 2 concentrates on additional types of equations, such as exponential and logarithmic equations. |
| Algebra 1 is essential to understand algebra 2. | Algebra 2 is essential for understanding concepts coming on calculus. |
Tips and Tricks on Algebra 1
- To understand Algebra 1, we need to be familiar with the pre-algebra topics like integers, one-step equations, multistep equations, inequalities and equations, graphs and functions, percent, probabilities, an introduction to geometry, and, right triangles. Once we go through a refresher, then we can proceed to algebra 1.
- When multiplying two rational expressions in algebra, there is always a risk of getting false solutions or extraneous solutions so be careful with your calculations part.
- We can add polynomials by just adding the like terms to combine the two polynomials into one.
Important Notes on Algebra 1:
- The addition property of inequality: Adding the same number to each side of the inequality produces an equivalent inequality.
- Negative exponents: The reciprocals of the positive exponents in exponential functions.
- The quotient of powers property: It tells us that when we divide the powers with the same base we just have to subtract the exponents.
- The constants have a monomial degree of 0.
☛ Related Topics:
Algebra 1 Problems
-
Example 1: Using laws and properties of algebra 1, evaluate the expression (4 × (x + 2)), where x = 5.
Solution:
Given, x = 5. Putting the value of x in 4 × (x + 2), we get, 4 × (5 + 2) = 4 × 7 = 28.
Answer: 28
-
Example 2: Solve the given expression for the value of x, 4 + 3 = x.
Solution:Given, 4 + 3 = x. We will simply do the addition of the given expression and get the value of x. 4 + 3 is equal to 7, or x = 4 + 3 = 7.
Answer: Therefore, the value of x is 7.
-
Example 3: Solve the given expression using rules of algebra 1 for the value of y, 2y + 16 = 32.
Solution:
Given, 2y + 16 = 32. We will solve the equation for y.
2y = 32 - 16 gives 2y = 16, y = 8.
Answer: Therefore, the value of y is 8.

FAQs on Algebra 1
What Will You Learn in Algebra 1?
Algebra 1 or Elementary algebra includes the basic traditional topics studied in the modern elementary algebra course. Basic arithmetic operations comprise numbers along with mathematical operations such as +, -, x, ÷. While, algebra involves variables as well like x, y, z, and mathematical operations like addition, subtraction, multiplication, and division to form a meaningful mathematical expression.
What is Considered Algebra 1?
Algebra 1 consists of the general concepts of algebra. It introduces evaluating equations and inequalities, real numbers, and their properties, which include additive and multiplicative identities, inverse operations, and the distributive and commutative properties.
What is the Difference Between Algebra 1 and Algebra 2?
The difference between Algebra 1 and Algebra 2 can be understood using the following points:
- Algebra 1 helps students to have the basic command in algebra topics, while algebra 2 increases complexity and understanding of the topics learned in algebra 1.
- In algebra 1, students learn how to manipulate exponents or polynomials and write them in simpler forms, etc, while in Algebra 2, students learn to apply the skills thus obtained in algebra 1 and also learn more difficult techniques.
- Algebra 1 is concentrated on solving equations and inequalities. But, algebra 2 concentrates on additional types of equations, such as exponential and logarithmic equations.
- Algebra 1 is essential to understand algebra 2, whereas, algebra 2 is essential for understanding concepts coming on calculus.
What is Standard Form in Algebra 1?
A standard form in Algebra 1 is a form of writing a given mathematical concept like an equation, number, or an expression in a form that follows certain rules.
How to Learn Algebra 1 Fast?
The concepts of algebra 1 can be mastered by following certain instructions. The key points given below will help you ensure a thorough graphing of elementary algebra.
- Focus on basic arithmetic concepts.
- Remember PEMDAS rule.
- Learn to distinguish clearly between the roles of variables, constants, exponents, and negative and positive numbers.
- Do a thorough revision of formulas.
- Work on practice problems.
What Grade is Algebra 1?
Algebra 1 or elementary algebra is the first math class you are required to take as part of your middle school. We study real numbers, exploring solving, writing, and graphing linear equations in this part of Algebra. Also, polynomials, as well as quadratic equations and functions are included in Algebra 1.
What Topics are Covered in Algebra 1?
The topics covered in algebra 1 are divided into different chapters. These chapters can be broadly classified into the following categories:
- Real Numbers and Their Operations
- Linear Equations and Inequalities
- An Introduction To Functions
- Graphing Lines
- Solving Linear Systems
- Polynomials and Their Operations
- Factoring and Solving by Factoring
- Exponents And Exponential Functions
- Rational Expressions and Equations
- Radical Expressions and Equations
- Solving Quadratic Equations and Graphing Parabolas
- Data Analysis And Probability
Is Algebra 1 or 2 Harder?
Algebra 1 is the building block of algebra 2. Algebra 2 is a higher and more complex course, hence algebra 2 is a lot harder than algebra 1.
What is Algebra 1 Equations?
The equations of algebra 1 include only linear equations and quadratic equations. Cubic equations and other higher-order equations are NOT a part of algebra 1.
What is the First Thing you Learn in Algebra 1?
The first thing students learn in algebra 1 is real numbers and their operations.
What are the Prerequisites to Understand Algebra 1 Better?
To understand Algebra 1, it is an advantage if you know the foundations of arithmetic, integers, fractions, decimals, percent, ratio, proportion, probabilities, an introduction to geometry, and, right triangles.
visual curriculum