Rationalization
Rationalization is a process that finds application in elementary algebra, where it is used to eliminate the irrational number in the denominator. There are many rationalizing techniques which are used to rationalize the denominator. The word rationalize literally means making something more efficient. Its adoption in mathematics means making the equation reduced into its more effective and simpler form.
| 1. | Rationalization |
| 2. | Rationalizing a Surd |
| 3. | How to Rationalize Denominator? |
| 4. | Solved Examples |
| 5. | Practice Questions |
| 6. | FAQs on Rationalization |
Rationalization
Rationalization can be considered as the process used to eliminate a radical or an imaginary number from the denominator of an algebraic fraction. That is, remove the radicals in a fraction so that the denominator only contains a rational number. Let us recall some important terms relating to the concept of rationalization in this section.
Radical
A radical is an expression that uses a root, such as a square root, cube root. For example, an expression of the form: √(a + b) is radical.
Radicand
Radicand is the term we are finding the root of. For example, In the following figure, (a + b) is the radicand.
Radical Symbol
The √ symbol means "root of". The length of the horizontal bar is important. The length of the bar signifies variables or constants that are a part of the root function. The variables or constants that are not under the root symbol are hence not part of the root.
Degree
The degree is the number depicted in the figure below. 2 means square root, 3 means cube root. Further, they are referred to as 4th root, 5th root, and so on. If this is not mentioned, we take it as square root by default.
Conjugate
A math conjugate of any binomial means another exact binomial with the opposite sign between its two terms. For example, the conjugate of (x + y) is (x - y) or vice versa. Thus, both these binomials are conjugates of each other.
Rationalizing a Surd
Surds are irrational numbers that cannot be further simplified in their radical form. For example, an irrational number √8 can be simplified further as 2√2, whereas √2 cannot be simplified any further. Thus √2 is a surd.
Examples of a monomial radical: √6, 3√2, \(\sqrt[3]{2}\)
Examples of a binomial radical: √3 + √6, 1 - √2
The procedure to rationalize an expression depends on the radical if that is monomial or binomial.
Rationalizing a Monomial Radical
To rationalize a surd or radical, in the denominator, different steps are to be followed depending upon the degree of the polynomial or the fact that if the radical is a monomial or polynomial. Any polynomial with only one term is called a monomial. \(\sqrt{2}\), \(\sqrt{7} \text x \), \(\sqrt[3]{7 \text x }\), etc. could be in the denominators.
Procedure:
1) Suppose the denominator contains a radical, as in this fraction:a/√ b. Here, the radical must be multiplied and divided by √ b and further simplified.
2) For a polynomial with a monomial radical in the denominator, say of the form, \( \text a \sqrt[ \text m ]{ \text x^ \text n }\), such that n < m, the fraction must be multiplied by a quotient containing \( \text a \sqrt[ \text m ]{ \text x^{ (\text m - \text n)} }\), both in the numerator and denominator. This gives us the result \( \text a \sqrt[ \text m ]{ \text x ^ \text m}\), which can be replaced by \( \text x \) and hence free of the radical term.
Let us go through this technique step by step using the following examples.
Example: Let us rationalize the fraction: 2/√7.
Step 1. Examine the fraction - The given fraction has a monomial radical √7 in the denominator that should be rationalized. Note that the numerator can have a radical, so you don't need to worry about the numerator while examining the fraction or simplifying it.
\(\dfrac{2 \times \sqrt{7}}{\sqrt{7} \times \sqrt{7}}\)
Step3. Simplify the expression as needed.
\(\dfrac{2 \times \sqrt{7}}{\sqrt{7} \times \sqrt{7}} = \dfrac{2\sqrt{7}}{7}\)
Rationalizing a Binomial Radical
If the denominator has a radical expression of the form \( \text a +\sqrt{ \text b}\) or \( \text a+ \text i \sqrt{ \text b}\), the fraction must be multiplied by the conjugate of the expression i.e., \( \text a -\sqrt{ \text b }\) or \( \text a - \text i \sqrt{ \text b }\) both in the numerator and denominator.
Procedure: Suppose the denominator contains a radical expression, (a + √b) or (a + \(i\)√b). Here, the radical must be multiplied by its conjugate.
Example: Let us have a look at the following fraction, \(\dfrac{5}{2-\sqrt{3}}\). The denominator needs to be rationalized. \(\dfrac{5}{2-\sqrt{3}}\times \dfrac{2+\sqrt{3}}{2+\sqrt{3}}\). This is further simplified and evaluated as 5(2 + √3).
The denominator is further expanded following the suitable algebraic identities.
Example: Let us learn the technique to rationalize the following fraction: \(\frac{\sqrt{7}}{2 + \sqrt{7}}\)
Step1. Examine the fraction - The denominator of the above fraction has a binomial radical i.e., is the sum of two terms, one of which is an irrational number.
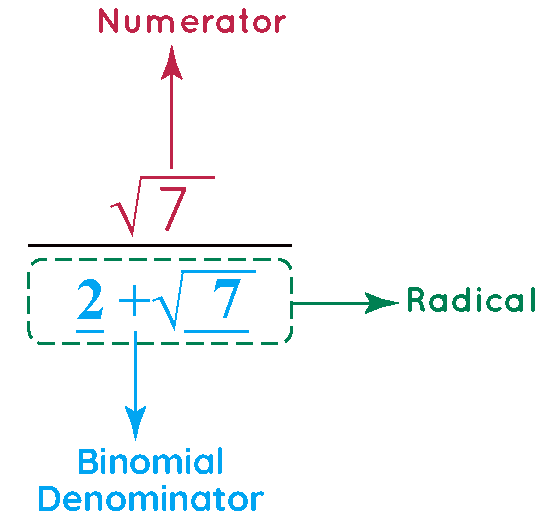
Step2. Multiply the numerator and denominator of the fraction with the conjugate of the radical.
\(\dfrac{\sqrt{7}}{2 + \sqrt{7}} \times \dfrac{2 - \sqrt{7}}{2 - \sqrt{7}}\)
Step3. Simplify the expression as needed.
\(\dfrac{\sqrt{7}}{2 + \sqrt{7}} \times \dfrac{2 - \sqrt{7}}{2 - \sqrt{7}}\)
Using difference of squares algebraic property, [(a + b)(a - b) = a2 - b2]
\(\dfrac{\sqrt{7}}{2 + \sqrt{7}} \times \dfrac{2 - \sqrt{7}}{2 - \sqrt{7}}\) = \(\dfrac{2\sqrt{7} - \sqrt{7} \times \sqrt{7}}{(2)^2 -\sqrt{7}^2}\)
= \(\dfrac{2\sqrt{7} - 7}{4 - 7}\)
= \(\dfrac{7 - 2\sqrt{7}}{3}\)
Rationalizing a Cube Root
This method can be generalized to roots of any order while rationalizing. For the given fraction with cube root radical in the denominator, \(\dfrac{1}{\sqrt[3]{5}}\), we can follow the given steps,
Step1. Examine the fraction - The fraction has a radical in the form of a cube root in the denominator.
\(\dfrac{1}{\sqrt[3]{5}} \times \dfrac{5^{2/3}}{5^{2/3}}\)
Step3. Simplify the expression as needed.
\(\dfrac{1}{\sqrt[3]{5}} \times \dfrac{5^{2/3}}{5^{2/3}}\) = \(\dfrac{5^{2/3}}{5^{1/3} \times 5^{2/3}}\)
= \(\dfrac{5^{2/3}}{5^{1/3 + 2/3}}\)
= \(\dfrac{5^{2/3}}{5}\)
= \(\sqrt[3]{25}\)/5
How to Rationalize Denominator?
When you look at the definition of "rationalize", it will become clearer as to what exactly rationalizing a denominator means. The numbers like \(\frac{1}{2}\), 5 and 0.25 are all rational numbers i.e., they can be expressed as a ratio of two integers like \( \frac{1}{2}, \frac{5}{1}, \frac{1}{4} \) respectively . Whereas, some radicals are irrational numbers because they cannot be represented as the ratio of two integers. Thus, the denominator needs to be rationalized to make the expression become a rational number. The following table gives the equivalent rational values of an irrational number.
| Irrational | Rational |
|---|---|
| \(\dfrac{1}{\sqrt{7}}\) | \(\dfrac{\sqrt{7}}{7}\) |
| \(\dfrac{4}{\sqrt{3}}\) | \(\dfrac{4 \sqrt{3}}{3}\) |
| \(\dfrac{4 + \sqrt{7}}{\sqrt{7}}\) | \(\dfrac{4 \sqrt{7} + 7}{7}\) |
The steps given below can be followed to rationalize the denominator in a fraction,
- Step 1: Multiply the denominator and numerator by a suitable radical that will remove the radicals in the denominator.
- Step 2: Make sure all surds in the fraction are in the simplified form.
- Step 3: You can simplify the fraction further if needed.
Related Articles on Rationalization
Check out the following pages related to rationalization
Important Notes
Here is a list of a few points that should be remembered while studying rationalization:
- Rationalization can be considered as the process used to eliminate a radical or imaginary number from the denominator of an algebraic fraction. That is, remove the radicals in a fraction so that the denominator only contains a rational number.
- A radical is an expression that uses a root, such as a square root, cube root. For example, an expression of the form: √(a + b) is radical.
- A math conjugate of any binomial means another exact binomial with the opposite sign between its two terms
FAQs on Rationalization
What Is Rationalization Method?
Rationalization is the process of removing a radical or surd from the denominator and shifting it to the numerator. By rationalizing, we make a denominator of a fraction as a rational number.
What Is Method to Rationalize Radicals in Denominators?
The radical present in the denominator of a fraction can be rationalized in the following way,
- Step 1: Multiply numerator and denominator by a suitable radical that will remove the radicals in the denominator.
- Step 2: Make sure all radicals are in the simplified form.
- Step 3: Simplify the fraction further if needed.
How Do You Rationalize Surds?
When the denominator of a fraction contains a surd, both numerator and denominator are multiplied with that value. The denominator product is solved, thereby giving a rationalized denominator.
Why Do We Rationalize Denominators?
If the denominator is linear in terms of a radical, both numerator and denominator are multiplied with a value such that the denominator product is expanded and becomes rationalized. For the denominator with a radical expression of the form a + √b or a + \(i\)√b, the fraction must be multiplied by the conjugate of the expression i.e., a - √b or a - \(i\)√b.
What Are the Rules of Rationalization?
The following rules can be followed while rationalizing a denominator,
- Check if all the radical or surds are in simplified form.
- Find the suitable radical and multiply it in the numerator and denominator that will remove the radicals in the denominator.
What Is an Example of Rationalization?
Any fraction with an irrational number in the denominator can be rationalized to remove the radical from the denominator. For example, The fraction √(36/7) can be simplified by rationalization as,
- Step 1: Simplify the given fraction as 6/√7.
- Step 2: Multiply the numerator and denominator by √7, to give 6√7/7
Why Do We Rationalize Surds?
We rationalize the surds or radicals present in the denominator of a fraction, to make the denominator a rational number. In order to do so, we generally multiply both numerator and denominator by a suitable radical and simplify.