Degree of Polynomial
Polynomials are one of the significant concepts of mathematics, and so is the degree of polynomials, which determines the maximum number of solutions a function could have and the number of times a function will cross the x-axis when graphed. It is the highest exponential power in the polynomial equation. Let us learn in detail about this concept and how to find the degree of a polynomial.
| 1. | What is Degree of a Polynomial? |
| 2. | How to Find the Degree of a Polynomial? |
| 3. | Classification Based on Degree of Polynomial |
| 4. | Degree of a Polynomial Applications |
| 5. | FAQs on Degree of a Polynomial |
What is Degree of Polynomial?
The degree of a polynomial is the highest exponential power in the polynomial equation. Only variables are considered to check for the degree of any polynomial, coefficients are to be ignored. For an nth degree polynomial function with real coefficients and x as the variable having the highest power n, where n takes whole number values, the degree of a polynomial p (x) = anxn + an-1xn-1 + an-2xn-2 + ... + a1x1 + a0 in standard form is given as 'n'.
Degree of a Polynomial Definition
The degree of a polynomial is the greatest power of a variable in the polynomial equation. To determine the degree of a polynomial function, only the terms with variables are considered to find out the degree of polynomial. The highest exponential power of the variable term in the polynomial indicates the degree of that polynomial.
Look at the polynomial function given below, where the highest power of x is n. Hence, n is the degree of polynomial in this function.
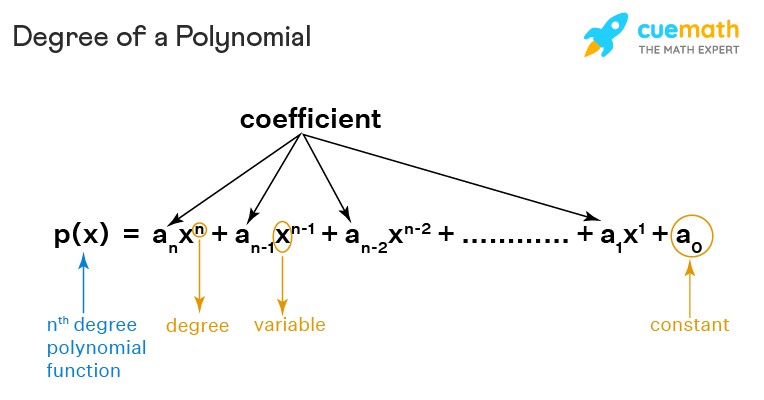
How to Find the Degree of Polynomial?
Consider the polynomial: p(x): 2x5−12x3+3x−π. The term with the highest power of x is 2x5 and the corresponding (highest) exponent is 5. Therefore, we will say that the degree of this polynomial is 5. Thus, the degree of a polynomial is the highest power of the variable in the polynomial. We can represent the degree of a polynomial by Deg(p(x)). Given below are some examples:
- Deg(x3+1) = 3
- Deg(1+x+x2+x3+...+x50) = 50
- Deg(x+π3) = 1
Note that the degree is the highest exponent of the variable term, so even though the exponent of π is 3 (refer to the last example given above), that is irrelevant to determine the degree of the polynomial.
Degree of Zero Polynomial
When all the coefficients are equal to zero, the polynomial is considered to be a zero polynomial. It is of the form f(x) = 0. We can write it as:
- f(x) = 0x0
- f(x) = 0x1
- f(x) = 0x2
- and so on.
By this time, you might have understood that the degree of a zero polynomial cannot be defined. So, the degree of the zero polynomial is either undefined or sometimes it is defined in a way that is negative (-1 or -∞).
Degree of Constant Polynomial
A constant polynomial (P(x) = c) has no variables. Since there is no variable, there is no power to it. So it can be written as P(x) = Cx0 as x0 = 1. Thus, the degree of the constant polynomial is zero. For example: For 6 or 6x0, degree = 0.
Degree of a Polynomial With More Than One Variable
The degree of a polynomial with more than one variable can be calculated by adding the exponents of each variable in it. For example: 5x3 + 6x2y2 + 2xy.
- 5x3 has a degree of 3 (x has an exponent of 3).
- 6x2y2 has a degree of 4 (x has an exponent of 2, y has 2, so 2+2=4).
- 2xy has a degree of 2 (x has an exponent of 1, y has 1, so 1+1=2).
The largest degree out of those is 4, so the polynomial has a degree of 4.
Classification Based on Degree of Polynomial
Each of the polynomials has a specific degree and based on that they have been assigned a specific name. Let's classify the polynomials based on the degree of a polynomial with examples.
| Polynomials | Degree | Examples |
|---|---|---|
| Constant Polynomial | Polynomials with Degree 0 | 3 |
| Linear Polynomial | Polynomials with Degree 1 | x + 8 |
| Quadratic Polynomial | Polynomials with Degree 2 | 3x2 - 4x + 7 |
| Cubic Polynomial | Polynomials with Degree 3 | 2x3 + 3x2 + 4x + 6 |
| Quartic Polynomial | Polynomials with Degree 4 | x4-16 |
| Quintic Polynomial | Polynomials with Degree 5 | 4x5+ 2x3 - 20 |
Degree of a Polynomial Applications
Given below are a few applications of the degree of a polynomial:
- To determine the maximum number of solutions that a function could have.
- To determine the maximum number of times a function will cross the x-axis when graphed.
- To check whether the polynomial expression is homogeneous, determine the degree of each term. When the degrees of the term are equal, then the polynomial expression is homogeneous and when the degrees are not equal, then the expression is said to be non-homogenous. For example, in 4x3 + 3xy2+8y3, the degree of all the terms is 3. Hence, the given example is a homogeneous polynomial of degree 3.
Degree of Polynomial Tips and Tricks:
In order to find the degree of a polynomial, you can follow these steps:
- Identify each term of the given polynomial.
- Combine all the like terms, the variable terms; ignore constant terms.
- Arrange those terms in descending order of their powers.
- Find the term with the highest exponent and that defines the degree of the polynomial.
Important Notes on Degree of Polynomial:
- Degree of a polynomial with only one variable: The largest exponent of the variable in the polynomial (using Descartes' rule of signs)
- Degree of a polynomial with more than one variable: Add the exponents of each variable given in a term, and find which term has the greatest degree. That will be considered as the degree of the polynomial.
- Degree of a rational expression: Take the degree of the top (numerator) and subtract the degree of the bottom (denominator).
☛Related Articles:
Check these interesting articles related to the concept of the degree of polynomials in math.
Degree of a Polynomial Examples
-
Example 1: Determine the leading coefficient and the degree of the polynomial of the following polynomial 5x2 - 20x - 20.
Solution:
Given a polynomial expression, 5x2 - 20x - 20. The highest exponent of the variable x is 2, and so the degree of the polynomial is 2. The coefficient with the highest exponent will be the leading coefficient of the polynomial, so the leading coefficient is 5.
Answer: Therefore, degree = 2 and leading coefficient = 5.
-
Example 2: Find the degree of the polynomial 5x4 + 3x2 - 7x5 + x7.
Solution:
In order to find the degree, check each term of the given polynomial. All are unlike terms with x as a variable. Arrange these terms in descending order of their powers, which gives x7 - 7x5 + 5x4+ 3x2. The term with the greatest or highest exponent is x7.
Answer: Therefore, the degree of the polynomial is 7.
-
Example 3: Find a fourth-degree polynomial satisfying the following conditions: has roots (x-2), (x+5) and should be divisible by 4x2.
Solution:
We are already familiar with the fact that a fourth-degree polynomial is a polynomial with degree 4. Also, we know that we can find a polynomial expression by its roots.
First condition: (x-2) (x+5) = x(x+5) - 2(x+5) = x2+5x-2x-10 = x2+3x-10.
Second condition: (x2+3x-10)(4x2) = x2.4x2 + 3x.4x2 - 10.4x2 = 4x4+12x3-40x2Answer: Therefore, the required polynomial is 4x4 + 12x3- 40x2.

FAQs on Degree of Polynomial
What is the Degree of a Polynomial?
The degree of a polynomial is the highest degree of the variable term with a non-zero coefficient in the polynomial.
What is the Degree of a Quadratic Polynomial?
Quadratic polynomials are characterized as polynomials with degree 2. Thus, the degree of a quadratic polynomial is 2.
What is Degree 3 Polynomial?
Degree 3 polynomials are known as cubic polynomials. They have 3 as the highest exponent of the variable. One example of a degree of the polynomial 3 is x3 + 5x - 20.
How to Find the Degree of a Polynomial With More Than One Variable?
Sometimes, a polynomial will have multi variables. In that case, add the exponents of all variables to calculate the degree of each term. Then the highest degree is the degree of the polynomial. Consider the example below.
Example: Find the degree of polynomial 5xy - 7x2y + 10x2 y3.
Solution:
Let us compute the degree of each term by adding exponents.
- Degree of 5xy (= 5x1y1) is 1 + 1 = 2.
- Degree of 7x2y (= 7x2y1) is 2 + 1 = 3.
- Degree of 10x2 y3 is 2 + 3 = 5.
Among all these degrees, 5 is the highest number and hence the degree of the given polynomial is 5.
What is the Degree of the Zero Polynomial?
A zero polynomial has all its variable coefficients equal to zero. It is a constant polynomial having a value of 0. Thus, the degree of the zero polynomial is undefined.
What is the Degree of Polynomial 5x4?
For the polynomial 5x4, the exponent with variable x is 4. Thus, the degree of polynomial 5x4 is 4.
What is the Degree of the Polynomial 5√3?
The degree of polynomial 5√3 is zero as there is no variable and the degree of any polynomial is defined by the highest exponential power of its variable term. Also, the degree of any constant is 0.
Why is the Degree of a Polynomial Important?
The degree of a polynomial function has great importance as it determines the maximum number of x-intercepts that a function could have and the maximum number of times a function crosses the x-axis on graphing it.
Why is the Degree of a Constant Polynomial?
A constant polynomial is a polynomial that has just a constant in it. A constant function is of the form f(x) = c and it can be written as f(x) = cx0. Here, the highest exponent itself is 0 and hence the degree of a constant polynomial is 0.
visual curriculum