nth Degree Polynomial

A polynomial is the parent term used to describe a certain type of algebraic expressions that contain variables, constants, and involve the operations of addition, subtraction, multiplication, and division along with only positive powers associated with the variables.

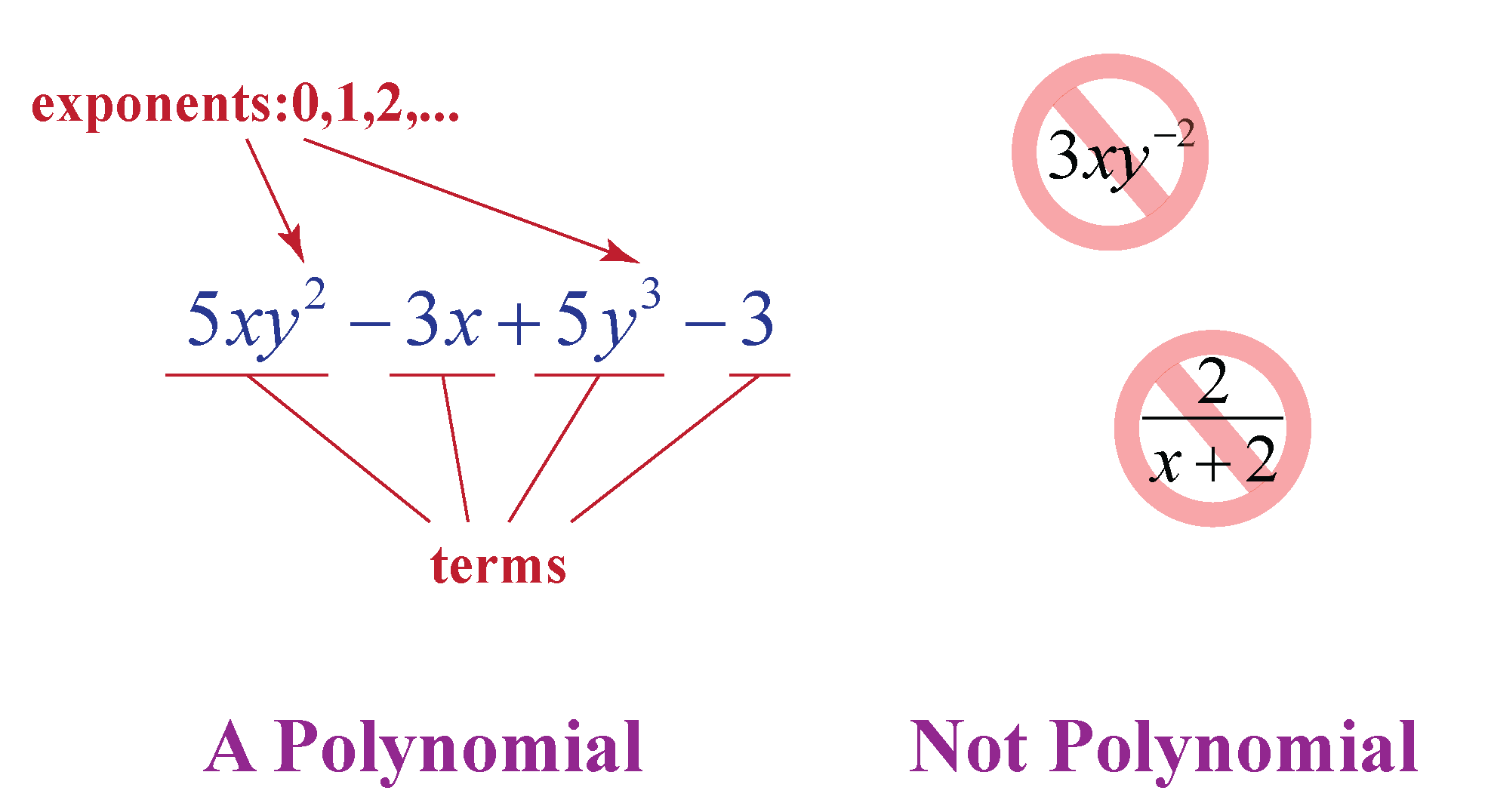
In this mini-lesson, we will study about the nth degree polynomials using nth degree polynomial definition and nth degree polynomial examples.

Check-out interactive examples on nth degree polynomial function with real coefficients. Do try your hand at a few practice questions at the end of the page.

Lesson Plan

Nth Degree Polynomials: Definition

The degree of a polynomial is defined as the highest power of the variable in the polynomial. 

Thus, Nth degree polynomial is any polynomial with the highest power of the variable as \(n\). 

This means that any polynomial of the form:

\(P(x) = a_n x^n + a_{n-1} x^{n-1} + a_{n-2} x^{n-2} + .... + a_0 \)

is an nth degree polynomial function with real coefficients and the variable is represented as \( x \), having highest power \(n\).

\(n\) will take all whole number values.

For example: Expressions, like \( \sqrt{x} + 2x + 7\), are not a polynomial because all the powers of variable \(x\) are not whole numbers. 

\(a_n, a_{n-1}, a_{n-2}, ..., a_0\) are the coefficients that take numerical values as their inputs.

This is also the generalized way to represent different types of polynomials, i.e., coefficients \(a_n, a_{n-1}, a_{n-2}, ..., a_0\) and the power \( n \) can have numerical values depending upon the types of polynomials they represent.

Nth Degree Polynomials: Examples

Cubic polynomial: A cubic polynomial can be generally interpreted as a form of nth degree polynomial with the value of \(n\) as 3:

Quadratic polynomial: A quadratic polynomial can be generally interpreted as a form of nth degree polynomial with the value of \(n\) as 2

---

The general form used to represent nth degree polynomial is,

\(P(x) = a_n x^n + a_{n-1} x^{n-1} + a_{n-2} x^{n-2} + .... + a_0 \)

 Here, \(a_0, a_1, a_2, ..., a_n\) are the coefficients that take numerical values as their inputs, \( x\) is the variable, and \(n\) is the degree of the polynomial, which is a whole number.

General form: \(P(x)\) = \(a_n x^n + a_{n-1} x^{n-1} + a_{n-2} x^{n-2} + .... + a_0 \)

The following table shows few nth degree polynomials for different values of \(n\),

Polynomial	Degree( Values of n)	Example
Zero Polynomial	not defined	\(P(x) = 0 \)
Non-Zero Constant	0	\(P(x) = 5 \)
Linear Polynomial	1	\(P(x)\) = \(7x + 2 \)
Quadratic Polynomial	2	\(P(x)\) = \(x^2 - x + 5 \)
Cubic Polynomial	3	\(P(x)\) = \(2x^3 + 3x^2 + x - 3 \)
Quartic Polynomial	4	\(P(x)\)= \(3x^4 + 2x^3 + x^2 - x + 8 \)
Quintic Polynomial	5	\(P(x)\) = \(4x^5 + x^3 + x^2 - x \)
Hexic Polynomial	6	\(P(x)\) =\( x^6 + x^3 - x \)
Septic/Heptic Polynomial	7	\(P(x)\) = \(x^7 - x^6 - x \)
Octic Polynomial	8	\(P(x)\) = \(x^8 + x^7 - x^5 + x^3 \)
Nonic Polynomial	9	\(P(x)\) =\( x^9 + 4 \)
Decic Polynomial	10	\(P(x)\)= \(x^{10} - 4x + 2 \)

Zeros of Nth Degree Polynomial 

Zeros or roots of an nth degree polynomial are those values that make the value of polynomial as '0'.

For the given nth degree polynomial:

\(P(x) = a_n x^n + a_{n-1} x^{n-1} + a_{n-2} x^{n-2} + .... + a_0 \)

Zeros are defined as those \( \alpha, \beta, ... , n \) values which when replace \(x\) in \(P(x)\), would give '0'.

A polynomial of degree \( n \) will have \(n\) number of zeros.

Zeros of any polynomial can be found using its graphical representation. The number of times the graph intersects the x-axis is equal to the number of distinct zeros the polynomial has.

For example:

For the polynomial shown in the following graph: 

Number of distinct zeros = number of intersections of the graph with the x-axis.

Here, the graph intersects the x-axis 3 times, which means that the polynomial will have 3 distinct zeros at \(x = \) respectively.

Example 2

 

 

For what value of \(k\), -4 is the zero of the polynomial \(x^2 - 2x - (7k + 3)\)?

Solution

Zero of a polynomial \(P(x)\) gives the value of polynomial as '0' when substituted for \(x\).

Thus, for -4 to be the zero of the given polynomial,

\(\begin{align*} P(-4) = (-4)^2 - 2(-4) - (7p + 3 ) &= 0 \\ 16 +  8 -7k - 3 &= 0 \\ 7k &= 21 \\ k &= 3 \end{align*}\)

\(\therefore\) k = 3

Example 3

 

 

Write the number of zeros of the polynomial, \(y = f(x)\) in the following graph:

Solution

For the given graph:

 

The graph intersects the x-axis at 4 points, which means that for four different values of \(x\), the polynomial will have a '0' value.

Thus, these four points will be the zeros of the given polynomial in the graph.

Number of zeros of the polynomial = 4

 

\(\therefore\) Number of zeros of the polynomial = 4