Constant Function
A constant function is used to represent a quantity that stays constant over the course of time and it is considered to be the simplest of all types of real-valued functions. Constant functions are linear functions whose graphs are horizontal lines in the plane. The maximum marks which can be obtained in an examination can be taken as one of the real-life examples of constant functions.
A constant function has the same output even with different input values. In this article, let's learn about constant functions, their definition, and graphs with solved examples.
| 1. | What is a Constant Function? |
| 2. | How To Find a Constant Function |
| 3. | Graphs of Constant Functions |
| 4. | Characteristics of a Constant Function |
| 5. | FAQs on Constant Function |
What is a Constant Function?
A constant function is a function having the same range for different values of the domain. Graphically a constant function is a straight line, which is parallel to the x-axis. The domain of the function is the x-value and is represented on the x-axis, and the range of the function is y or f(x) which is marked with reference to the y-axis.

Any function can be considered as a constant function if it is of the form y = k, where k is a constant and k is any real number. It is also written as f(x) = k. We need to note here that the value of f(x) will always be 'k', and is independent of the value of x. In general, we can define a constant function as a function that always has the same constant value, irrespective of the input value.
Here are some of the examples of constant functions:
- f(x) = 0
- f(x) = 1
- f(x) = π
- f(x) = 3
- f(x) = −0.3412454
- f(x) equal to any other real number you can think about.
One of the interesting things about a constant function is that we can input any real number we want for x, and we can instantly know the value of the function at that x without using any calculations.
How to Find a Constant Function?
In this section, let's learn to differentiate between a constant function and a function that is not a constant function. To find if a function is a constant function, do the following:
- Check if it is possible to get different outputs for different inputs. If this is possible, then that is not a constant function
- But if it's only possible to get the same output irrespective of what the input values are, then it is a constant function.
(i) Consider the linear function y = x + 2. In this example, can we get different outputs by varying the input values? The answer is yes, because:
- If we input x = 1, we get y = 1 + 2 or y = 3
- If we input x = 2, then we get y = 2 + 2 or y = 4.
Since we get different outputs by varying the input values, this is NOT a constant function.
(ii) Consider the function y = 3. Here, we can notice that no matter what our x value is, or input, is, y will always be 3.
- If x = 3, y = 3
- if x = 5, y = 3
- y is always 3 no matter what our input is.
Since we can't get different outputs by varying the input values, this is a constant function.
Graphs of Constant Functions
You may be wondering how a constant function would look like on a coordinate plane. If you've ever seen a horizontal line in the graph, then what you've seen is the graph of a constant function. A constant function refers to a real-valued function with no variable in its definition. Let us consider the constant function f(x) = 3 where f: R → R.
- This means that it will always generate an output equal to 3, no matter what input values we provide
- So some points on its graph can be (-1, 3), (2, 3), (4, 3), etc.
Let us see the graph of the constant function f(x) = 3 below.

So the graph of f(x) = 3 is a horizontal line as the y-coordinates of all points are the same (as 3). Hence, the graphs of all constant functions are horizontal lines.
Characteristics of a Constant Function
All the constant functions cut through the vertical axis as per the value of their constant and they do not cut through the horizontal axis, as they are parallel to it. Also, the constant functions are continuous as they represent horizontal lines that extend continuously on both sides without any break. Here are some of the important characteristics of a constant function:
Slope of a Constant Function
A constant function is a linear function whose general format is y = mx + k, where m and k are constants. Thus, a constant function which is f(x) = k (or) y = k can be written as y = 0x + k. Comparing this equation with the slope-intercept form y = mx+b, we get its slope to be m = 0. Thus, the slope of a constant function is 0.
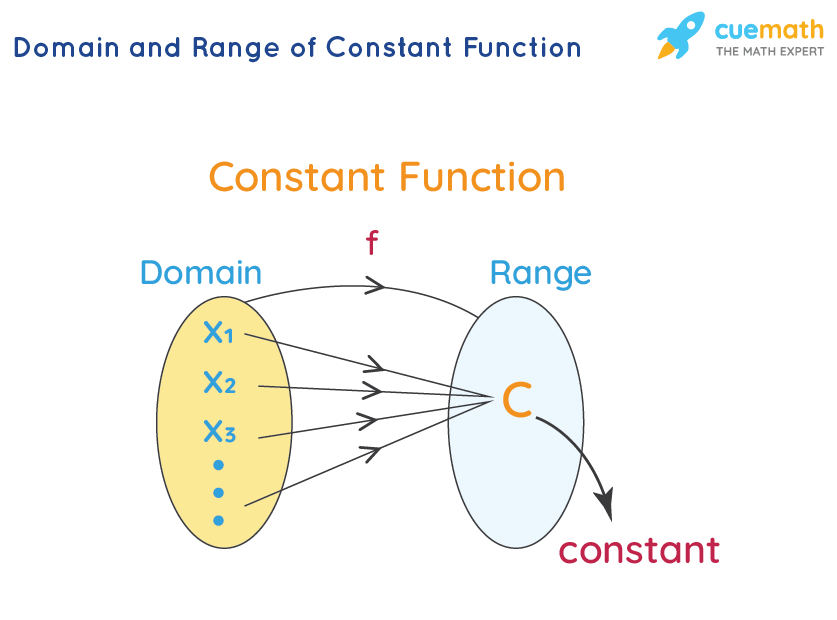
Domain and Range of a Constant Function
A constant function is a linear function whose range contains only one element irrespective of the number of elements of the domain. Since the constant function is defined for all real values of x:
- Its domain is the set of all real numbers, R. So, domain = R
- Since a constant function f(x) = k leads to only one output, which is k, its range is the set with just one element k. Range = {k}
Derivatives of a Constant Function
A constant function is the simplest of all functions and hence, its derivative is easier to compute. We can use the direct substitution to find the derivative of a constant function. The differentiation rule for a constant function f(x) is d/dx (c) = 0.
We can see from the above differentiation that the derivative of a constant function is zero. Also, the derivative is considered to be the slope of the tangent line of the function at any given point, and we already know that the slope of a constant function is always 0. Let us consider an example to understand the constant functions and their respective derivative. The constant function y = -1 and its derivative is y' = 0.
Limit of a Constant Function
According to the properties of limits, the limit of a constant function is equal to the same constant. For instance, if the function is y = 7, then the limit of this function is 7. This can be represented as: lim ₓ → ₐ C = C.
Constant Functions in Real World
There are so many places where constant functions find their application in real life. Here, constant functions are used to model situations where one parameter is constant and it isn’t dependent on the other independent parameters. Here are some examples of constant functions in the real world:
- The price of any item at a departmental store is $3.
- In a book sale, the price of any book is $10.
- An examination in which every student was given a star irrespective of how hard they all worked.
- A bag worth $30 is free for all purchases that go beyond $300.
- A school canteen where every child was given one sandwich irrespective of their grade or age
Important Notes on Constant Function:
Here is a list of a few points that should be remembered while studying the constant function
- The graph of a constant function can never be a curve.
- The graph of a constant function is always a horizontal line.
- An algebraic function is a constant function if there is no variable in its definition.
- The derivative of a constant function is 0.
- The integral of a constant function with respect to a variable is the variable itself.
☛ Related Topics:
Check out the following pages related to constant functions
Examples on Constant Function
-
Example 1: Which of the following functions is/are constant functions?
a) f(x) = x3 + 3
b) f(y) = y + (1/y)
c) f(y) = 5
d) f(x) = 3 + xSolution:
The correct option is c) f(y) = 5 since its values do not depend on the variable y. Its value remains 5 for any value of y.
Answer: Option c)
-
Example 2: Which of the following would represent the constant function(s)?

Solution:
We know that the graph of a constant function is always a horizontal line. Among the given graphs, only (d) and (e) are the horizontal lines. Therefore, the constant functions are (d) and (e).
Answer: (d) and (e).
-
Example 3: If f(x) = k is a constant function given that f(1) = 2, find k.
Solution:
The given function is,
f(x) = k
Substituting x = 1,
f(1) = k
But it is given that f(1) = 2. Substituting this in the above equation,
2 = k
Answer: k = 2.

FAQs on Constant Function
What is a Constant Function in Algebra?
A constant function is a function having the same value of range for different values of the domain. Graphically a constant function is a horizontal line, which is a straight line parallel to the x-axis.
What is the Equation of a Constant Function?
The equation of a constant function is of the form f(x) = k, where 'k' is a constant and any real number. Example of a constant function: f(x) = 4.
How Do You Know if a Function Is Constant?
A function is a constant function if:
- it has no variable in its definition and/or
- its graph is a horizontal line.
Is a Constant Function Linear?
Yes, a constant function is a linear function as the graphs of both constant and linear functions are straight lines in the plane. Thus, a constant function is always linear, in particular, it is always a horizontal line.
Is Constant Function Continuous?
Yes, a constant function is always continuous as its graph is a horizontal line and we can draw it without lifting our pen/pencil.
Can a Constant Function be Onto?
Yes, a constant function f(x) = k can be an onto function only when its codomain is as same as its range (which is {k}).
What is the Degree of Constant Function?
The degree of a constant function is zero as a constant k can be written as f(x) = kx0.
Is Constant Function Surjective?
No, a constant function is not surjective as it is not one-to-one. A constant function is a function whose output value remains the same for every input value provided to it. Hence, a constant function is not surjective. It can be surjective only if the codomain is equal to the range, that is, {k}.
Is Constant Function Injective?
No, a constant function is not injective. A constant function is a function in which, the output value is the same for every input value supplied to it. Since an injective function never actually maps two different input values to the same output value. Hence a constant function cannot be considered as injective. A constant function is injective only when the domain has only one element.
What is the Derivative of a Constant Function?
The derivative of any constant function is considered to be zero (dk/dx = 0)
What is the Integral of a Constant Function?
The integral of a constant function with respect to a variable is the constant times variable. i.e., ∫ k dx = kx + C, where C is the integration constant.
visual curriculum