A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.

Calculus Calculator

Calculus is one of the most important branches of mathematics, that deals with continuous change.

What is Calculus Calculator?

'Cuemath's Calculus Calculator' is an online tool that helps to calculate the value of limits, derivatives, indefinite, and definite integrals. Cuemath's online Calculus Calculator helps you to calculate the value of the derivatives in a few seconds.

NOTE: Enter the function with respect to x only.

How to Use Calculus Calculator?

Please follow the steps below on how to use the calculator:

  • Step 1: Choose a drop-down list to find the value of limits, derivatives, indefinite, and definite integrals.
  • Step 2: Enter the function in the given input boxes.
  • Step 3: Click on the "Calculate" button to find the values of limits, derivatives, indefinite, and definite integrals.
  • Step 4: Click on the "Reset" button to clear the fields and enter the different functions.

 

How to Find the limits, derivatives, indefinite integrals and definite integrals?

Limits are used as a way of making approximations used in the calculation as close as possible to the actual value of the quantity.

The limit formula to calculate the derivative of a function is:

​​​​​\(\lim_{x\rightarrow a} = A\)

It is read as “the limit of a function of x equals A as and when x approaches a.”

The derivative of a function is represented by f '(x). It means that the function is the derivative of y with respect to the variable x. The symbol dy and dx are called differentials. The process of finding derivatives is called differentiation.

There are common functions and rules we follow to find derivatives

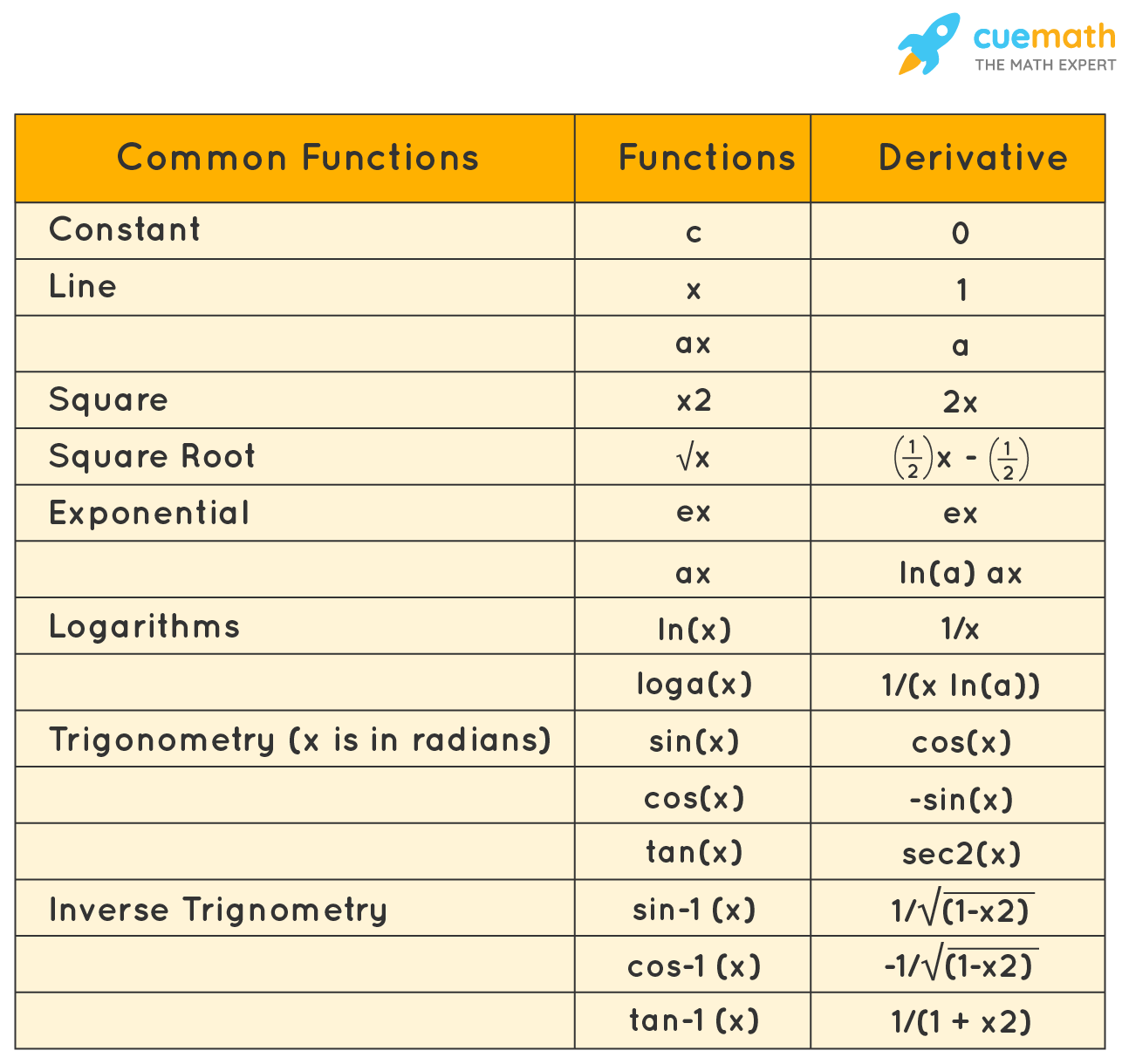
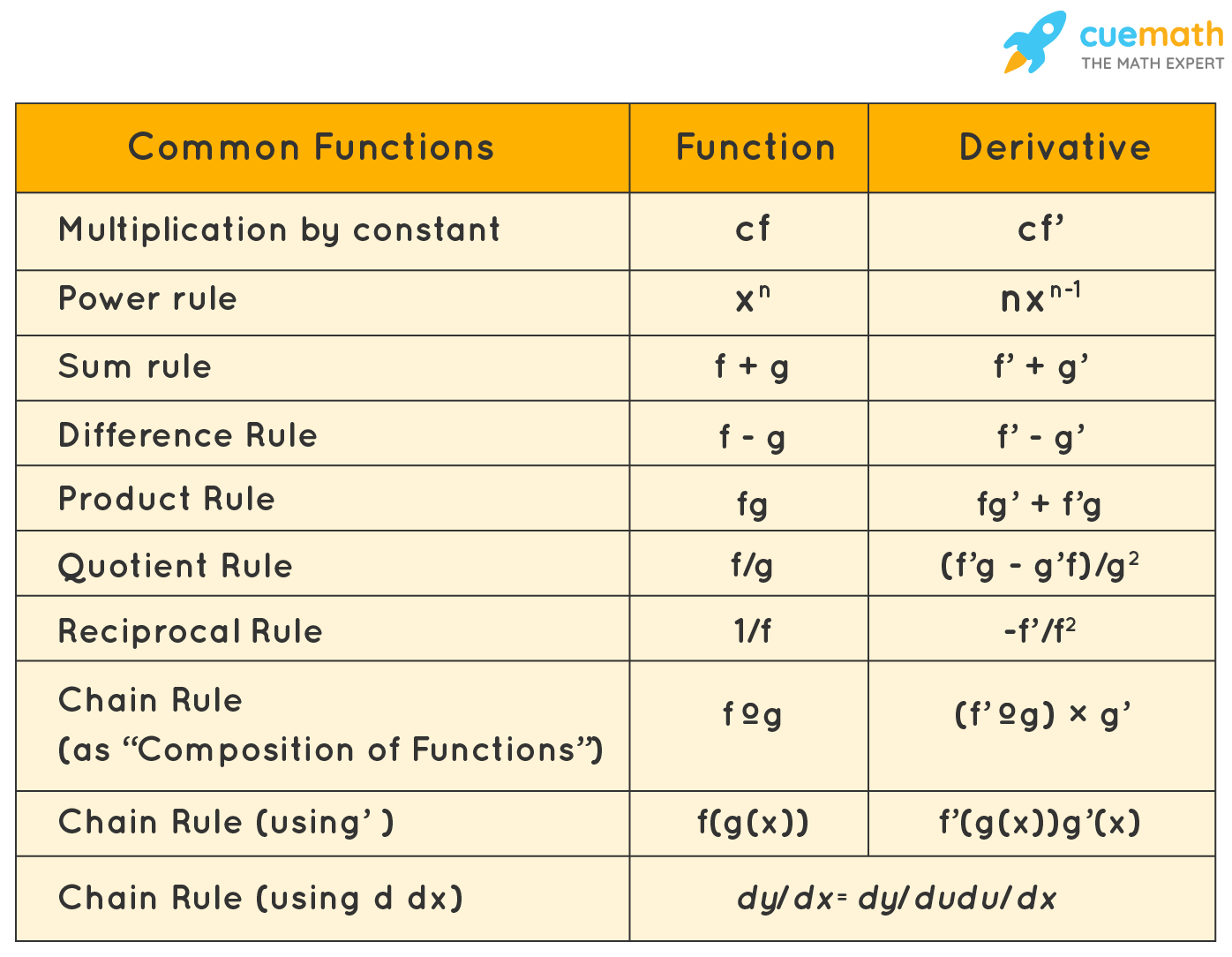
Integration is defined as the reverse process of differentiation. The integration is represented by ' ∫ '

The integrals are classified into 2 types: 1. Indefinite integral  2. Definite integral

Indefinite integrals: The integrals do not have any upper and lower limits. It is represented as ∫f(x)dx

Definite integrals: The integrals that have upper and lower limits. It is represented as \(\int\limits_a^b {f\left( x \right)dx}\)

The fundamental theorem of calculus tells us that to calculate the area under a curve y = f(x) from x = a to x = b, we first calculate the integration g(x) of f(x)

\(g\left( x \right)= \int {f\left( x \right)dx}\)

and then evaluate g(b) − g(a). That is, the area under the curve f(x) from x=a to x=b is \(\int\limits_a^b {f\left( x \right)dx = g\left( b \right) - g\left( a \right)}\)

There are common functions and rules we follow to find the integration.

Want to find complex math solutions within seconds?
Use our free online calculator to solve challenging questions. With Cuemath, find solutions in simple and easy steps.

Book a Free Trial Class

Solved Examples on calculus calculator

 

  1. Example1:

    Find the value of limit \(\lim_{x\rightarrow 2} (x^2 + 3x + 5) \)

    Solution:

    \(\lim_{x\rightarrow 2} (x^2 + 3x + 5) \)

    Substitute limit value 2 in given function f(x)

    = 22 + 3(2) + 5 

    = 4 + 6 + 5

    = 15

  2. Example2:

    Find the derivative value of 5x3 + 2x2

    Solution:

    = d / dx( 5x3 + 2x2)

    = d / dx ( 5x3) + d / dx(2x2)

    Using multiplication by constant and power rule,

    = (5 × 3x3 - 1) + (2 × 2x2 - 1)

    = 15x2 + 4x

  3. Example3:

    Find the integration value of 5x3 + 2x2

    Solution:

    = ∫( 5x3 + 2x2)

    = ∫( 5x3) + ∫(2x2)

    Using multiplication by constant and power rule,

    = [5 × (x3 + 1 / 3 + 1)] + [2 × x2 + 1 / 2 + 1]

    = 5x4 / 4 + 2x3 / 3

  4. Example4:
    Find the integration value of \(\int\limits_2^3 {(x + 3)\,dx}\)
    Solution:
    \(= \int\limits_2^3 {x dx} + \int\limits_2^3 {3dx}\)
    \(= \frac{x^2}{2}]_2^3 + 3 x]_2^3\)
    \(=\frac{1}{2} ( 3^2 - 2^2) + 3(3 - 2)\)
    = \(\frac{1}{2}(5) + 3\)
    \(=\frac{11}{2}\)
Show solution >

go to slidego to slidego to slidego to slide

Similarly, you can use the calculator to find the value of the limits, derivatives, indefinite, and definite integrals for:

  • ∫ x3 / 2
  • d / dx(5x2 + 6y2)
  • \(\lim_{x\rightarrow 4} (x^3 + 4x^2 + 7) \)
  •  ∫ x3 / 2 for limits x = 2 to x = 5
Related Articles:
 
Limits Calculator
 
Double Integral Calculator
Math worksheets and
visual curriculum