Continuous Function
A continuous function, as its name suggests, is a function whose graph is continuous without any breaks or jumps. i.e., if we are able to draw the curve (graph) of a function without even lifting the pencil, then we say that the function is continuous. Studying about the continuity of a function is really important in calculus as a function cannot be differentiable unless it is continuous.
Let us study more about the continuity of a function by knowing the definition of a continuous function along with lot more examples.
| 1. | What is Continuous Function? |
| 2. | Continuity in Calculus Examples |
| 3. | Properties of a Continuity |
| 4. | Theorems on Continuous Function |
| 5. | NOT Continuous Function |
| 6. | FAQs on Continuous Function |
What is Continuous Function?
A function f(x) is said to be a continuous function in calculus at a point x = a if the curve of the function does NOT break at the point x = a. The mathematical definition of the continuity of a function is as follows. A function f(x) is continuous at a point x = a if
- f(a) exists;
- limₓ → ₐ f(x) exists;
[i.e., limₓ → ₐ₋ f(x) = limₓ → ₐ₊ f(x)] and - Both of the above values are equal. i.e., limₓ → ₐ f(x) = f(a).
Is this definition really giving the meaning that the function shouldn't have a break at x = a? Let's see. "limₓ → ₐ f(x) exists" means, the function should approach the same value both from the left side and right side of the value x = a and "limₓ → ₐ f(x) = f(a)" means the limit of the function at x = a is same as f(a). These two conditions together will make the function to be continuous (without a break) at that point. You can understand this from the following figure.
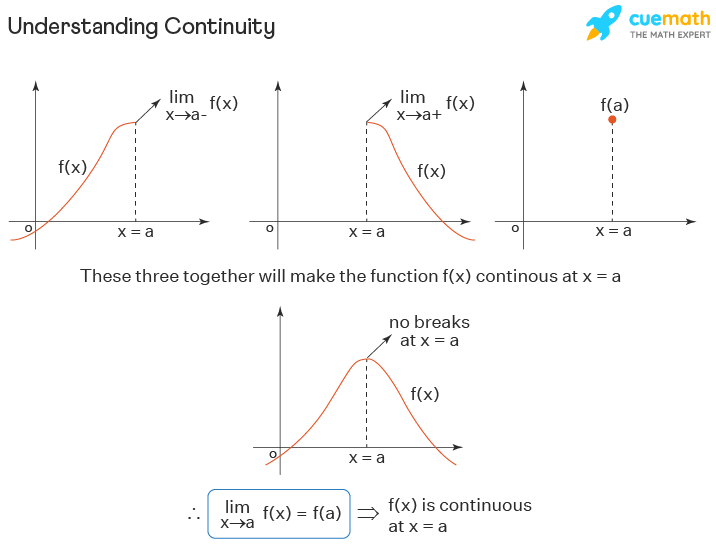
A function is said to be continuous over an interval if it is continuous at each and every point on the interval. i.e., over that interval, the graph of the function shouldn't break or jump.
Continuity in Calculus Examples
Here are some examples of functions that have continuity. All the functions below are continuous over the respective domains.

From the above examples, notice one thing about continuity: "if the graph doesn't have any holes or asymptotes at a point, it is always continuous at that point".
Properties of Continuity
Here are some properties of continuity of a function. If two functions f(x) and g(x) are continuous at x = a then
- f + g, f - g, and fg are continuous at x = a.
- f/g is also continuous at x = a provided g(a) ≠ 0.
- If f is continuous at g(a), then the composition function (f o g) is also continuous at x = a.
- All polynomial functions are continuous over the set of all real numbers.
- The absolute value function |x| is continuous over the set of all real numbers.
- Exponential functions are continuous at all real numbers.
- The functions sin x and cos x are continuous at all real numbers.
- The functions tan x, cosec x, sec x, and cot x are continuous on their respective domains.
- The functions like log x, ln x, √x, etc are continuous on their respective domains.
Theorems on Continuous Function
There are several theorems on a continuous function. Here are the most important theorems.
- Theorem 1: All polynomial functions are continuous on (-∞, ∞).
- Theorem 2: The functions ex, sin x, cos x, and arctan x are continuous on (-∞, ∞).
- Theorem 3: If two functions f and g are continuous on an interval [a, b], then the algebra of functions: f+g, f-g, and fg are continuous on [a, b]. But f/g is continuous on [a, b] given that f/g is NOT zero anywhere in the interval.
- Theorem 4: A rational function is continuous except at the vertical asymptotes.
NOT Continuous Function
A function that is NOT continuous is said to be a discontinuous function. i.e., the graph of a discontinuous function breaks or jumps somewhere. There are different types of discontinuities as explained below. By the definition of the continuity of a function, a function is NOT continuous in one of the following cases. We can see all the types of discontinuities in the figure below. From the figures below, we can understand that
- Removable discontinuity occurs at holes.
- Infinite discontinuity occurs at vertical asymptotes.

Jump Discontinuity
limₓ → ₐ₋ f(x) and limₓ → ₐ₊ f(x) exist but they are NOT equal. It is called "jump discontinuity" (or) "non-removable discontinuity".
Removable Discontinuity
limₓ → ₐ f(x) exists (i.e., limₓ → ₐ₋ f(x) = limₓ → ₐ₊ f(x)) but it is NOT equal to f(a). It is called "removable discontinuity".
Infinite Discontinuity
The values of one or both of the limits limₓ → ₐ₋ f(x) and limₓ → ₐ₊ f(x) is ± ∞. It is called "infinite discontinuity".
Important Notes on Continuity:
Here are some points to note related to the continuity of a function.
- A function is continuous at x = a if and only if limₓ → ₐ f(x) = f(a).
- It means, for a function to have continuity at a point, it shouldn't be broken at that point.
- For a function to be differentiable, it has to be continuous.
- All polynomials are continuous.
- The functions are NOT continuous at vertical asymptotes.
- The functions are NOT continuous at holes.
☛ Related Topics:
Here are some topics that you may be interested in while studying continuous functions.
Continuous Function Examples
-
Example 1: Check the continuity of the function f(x) = 3x - 7 at x = 7.
Solution:
Method 1:
Given that f(x) = 3x - 7 and x = 7 = a.
We will find the limₓ → ₐ f(x) and f(a).
limₓ → ₐ f(x) = limₓ → ₇ (3x - 7) = 3(7) - 7 = 21 - 7 = 14.
f(a) = f(7) = 3(7) - 7 = 21 - 7 = 14.
Therefore, limₓ → ₐ f(x) = f(a). Thus, f(x) is coninuous at x = 7.
Method 2:
We know that a polynomial function is continuous everywhere.
Here, f(x) = 3x - 7 is a polynomial function and hence it is continuous everywhere and hence at x = 7.
Answer: The function f(x) = 3x - 7 is continuous at x = 7.
-
Example 2: Prove that the following function is NOT continuous at x = 2 and verify the same using its graph. Also, mention the type of discontinuity. f(x) = \(\left\{\begin{array}{l}x-3, \text { if } x \leq 2 \\ 8, \text { if } x>2\end{array}\right.\)
Solution:
It is given that a = 2.
The given function is a piecewise function. Thus, we have to find the left-hand and the right-hand limits separately. Note that
- x → 2- ⇒ x < 2 ⇒ f(x) = x - 3 and
- x → 2+ ⇒ x > 2 ⇒ f(x) = 8.
Now we will compute the limits.
limₓ → ₂₋ f(x) = limₓ → ₂ (x - 3) = 2 - 3 = -1
limₓ → ₂₊ f(x) = limₓ → ₂ 8 = 8
Here, limₓ → ₂₋ f(x) ≠ limₓ → ₂₊ f(x).
Thus, limₓ → ₂ f(x) does NOT exist and hence f(x) is NOT continuous at x = 2.
Verification by Graph:

The function has jump discontinuity.
Answer: We proved that f(x) is a discontinuous function algebraically and graphically and it has jump discontinuity.
-
Example 3: Find the relation between a and b if the following function is continuous at x = 4. \(f(x)=\left\{\begin{array}{ll}a x-3, & \text { if } x \leq 4 \\ b x+8, & \text { if } x>4\end{array}\right.\)
Solution:
f(x) is a continuous function at x = 4. By continuity equation,
limₓ → ₄₋ f(x) = limₓ → ₄₊ f(x) = f(4)
limₓ → ₄ (ax - 3) = limₓ → ₄ (bx + 8) = a(4) - 3
a(4) - 3 = b(4) + 8 = a(4) - 3
From the first two expressions,
4a - 3 = 4b + 8
4a - 4b = 11
Answer: The relation between a and b is 4a - 4b = 11.

FAQs on Continuous Function
What is the Definition of Continuous Function?
A continuous function is a function whose graph is not broken anywhere. Mathematically, f(x) is said to be continuous at x = a if and only if limₓ → ₐ f(x) = f(a).
What is a Continuous Function Example?
The graph of a continuous function should not have any breaks. The polynomial functions, exponential functions, graphs of sin x and cos x are examples of a continuous function over the set of all real numbers.
What is Piecewise Continuous Function?
A continuous function is said to be a piecewise continuous function if it is defined differently in different intervals. For example, \(g(x)=\left\{\begin{array}{ll}(x+4)^{3} & \text { if } x<-2 \\8 & \text { if } x\geq-2\end{array}\right.\) is a piecewise continuous function.
What is the Definition of Continuity?
For the continuity of a function f(x) at a point x = a, the following 3 conditions have to be satisfied.
- f(a) exists
- limₓ → ₐ f(x) exists and
- limₓ → ₐ f(x) = f(a)
What is an Example of a NOT Continuous Function?
The function f(x) = [x] (integral part of x) is NOT continuous at any real number. Another example of a function which is NOT continuous is f(x) = \(\left\{\begin{array}{l}x-3, \text { if } x \leq 2 \\ 8, \text { if } x>2\end{array}\right.\)
Describe the Continuity of Square Root Function.
The graph of a square root function is a smooth curve without any breaks, holes, or asymptotes throughout its domain. Hence, the square root function is continuous over its domain.
Which Function is Always Continuous?
For a function to be always continuous, there should not be any breaks throughout its graph. For example, f(x) = |x| is continuous everywhere.
What is Continuous Function Formula?
A function f(x) is continuous at x = a when its limit exists at x = a and is equal to the value of the function at x = a. i.e., limₓ → ₐ f(x) = f(a)
Are Exponential Functions Continuous?
Yes, exponential functions are continuous as they do not have any breaks, holes, or vertical asymptotes.
visual curriculum