Logarithm
Logarithms is another way of writing exponents. We know that 25 = 32. But if we are asked to find what number replaces the question mark in 2? = 32, then by trial and error, we can simply find that the answer is 5. But what if we are asked to find the question mark in 2? = 30? Is there any number such that 2 raised to it gives 30? No, then how to solve it? The solution is logarithms (or logs).
Let us learn more about logarithms along with their properties with examples.
| 1. | What is Logarithm? |
| 2. | Logs Definition |
| 3. | Natural Log and Common Log |
| 4. | Rules of Logs |
| 5. | How to Condense/Expand Logarithms? |
| 6. | FAQs on Logarithms |
What is Logarithm?
Logarithm is nothing but another way of expressing exponents and can be used to solve problems that cannot be solved using the concept of exponents only. Understanding logs is not so difficult. To understand logarithms, it is sufficient to know that a logarithmic equation is just another way of writing an exponential equation.
Logarithm and exponent are inverse forms of each other. One can understand this from the section below. Initially, a mathematician named John Napier introduced logarithms for making calculations in a simple way and this concept is quickly adopted by other scientists, engineers, etc.

Here is the mathematical definition of logs.
Logs Definition
A logarithm is defined using an exponent.
- bx = a ⇔ logb a = x
Here, "log" stands for logarithm. The right side part of the arrow is read to be "Logarithm of a to the base b is equal to x".
A very simple way to remember this is "base stays as the base in both forms" and "base doesn't stay with the exponent in log form". Notice that 'b' is the base both on the left and right sides of the implies symbol and in the log form see that the base b and the exponent x don't stay on the same side of the equation.
Here,
- a and b are two positive real numbers.
- x is a real number.
- a, which is inside the log is called the "argument".
- b, which is at the bottom of the log is called the "base".

The above equation has two things to understand (from the symbol ⇔):
- bx = a ⇒ logb a = x. This is called "exponential to log form"
- logb a = x ⇒ bx = a . This is called "log to exponential form"
Here is a table to understand the conversions from one form to the other form.
| Exponential Form | Logarithmic Form |
|---|---|
| 25 = 32 | log2 32 = 5 |
| 62 = 36 | log6 36 = 2 |
| 3-2 = 1/9 | log3 (1/9) = -2 |
| e2 = 7.389 | loge 7.389 = 2 |
| 103 = 1000 | log10 1000 = 3 |
Natural Log and Common Log
Observe the last two rows of the above table. They have loge and log10. These two logs have specific importance and specific names in logarithms.
- loge is called the natural log
- log10 is called the common log
Let us study more about each of these.
Natural Logarithm
Natural logarithm is nothing but log with base e. That is, a natural log means loge. But it is not usually represented as loge. Instead, it is represented as ln. i.e.,
- loge = ln
Examples:
- ex = 2 ⇒ loge 2 = x (or) ln 2 = x.
- ex = 7 ⇒ loge 7 = x (or) ln 7 = x.
Common Logarithm
Common logarithm is nothing but log with base 10. That is, a common log means log10. But usually, writing "log" is sufficient instead of writing log10. i.e.,
- log10 = log
i.e., if there is no base for a log it means that its log10. In other words, it is a common logarithm.
Examples:
- 102 = 100 ⇒ log10 100 = 2 (or) log 100 = 2
- 10-2 = 0.01 ⇒ log10 0.01 = -2 (or) log 0.01 = -2
Observe that we have not written 10 as the base in these examples, because that's obvious.
Rules of Logs
The rules of logs are used to simplify a logarithm, expand a logarithm, or compress a group of logarithms into a single logarithm. Here are the rules (or) properties of logs. If you want to see how all these rules are derived, click here.
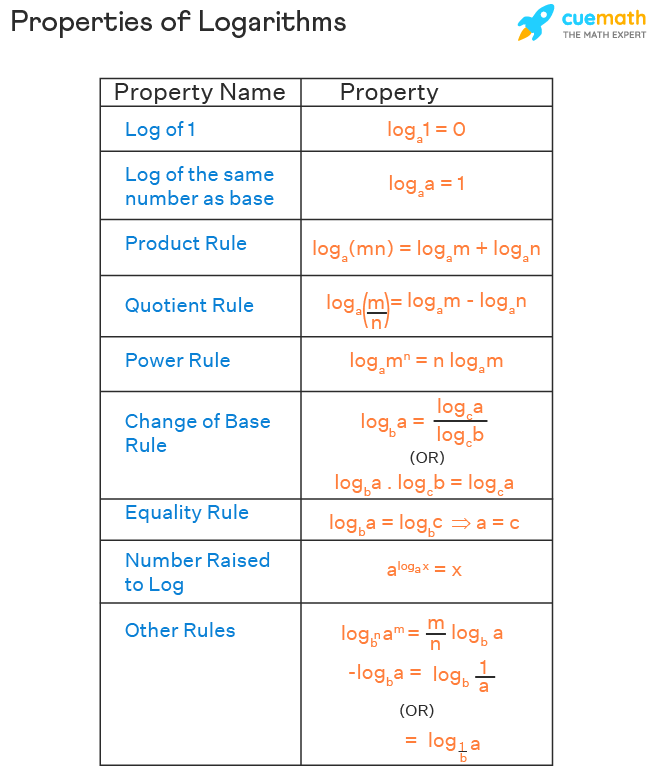
Let us see each of these rules one by one here.
Log 1
The value of log 1 irrespective of the base is 0. Because from the properties of exponents, we know that, a0 = 1, for any 'a'. Converting this into log form, loga 1 = 0, for any 'a'. Obviously, when a = 10, log10 1 = 0 (or) simply log 1 = 0.
When we extend this to the natural logarithm, we have, since e0 = 1 ⇒ ln 1 = 0.
Loga a
Since a1 = a, for any 'a', converting this equation into log form, loga a = 1. Thus, the logarithm of any number to the same base is always 1. For example:
- log2 2 = 1
- log3 3 = 1
- log 10 = 1
- ln e = 1
Product Rule of Log
The logarithm of a product of two numbers is the sum of the logarithms of the individual numbers, i.e.,
- loga mn = loga m + loga n
Note that the bases of all logs must be the same here. This resembles/is derived from the product rule of exponents: xm ⋅ xn = x m+n.
Examples:
- log 6 = log (3 x 2) = log 3 + log 2
- log (5x) = log 5 + log x
Quotient Rule of Log
The logarithm of a quotient of two numbers is the difference between the logarithms of the individual numbers, i.e.,
- loga (m/n) = loga m - loga n
Note that the bases of all logs must be the same here as well. This resembles/is derived from the quotient rule of exponents: xm / xn = x m-n.
Examples:
- log 4 = log (8/2) = log 8 - log 2
- log (x/2) = log x - log 2
Power Rule of Log
The exponent of the argument of a logarithm can be brought in front of the logarithm, i.e.,
- loga mn = n loga m
Here, the bases must be the same on both sides. This resembles/is derived from the power of power rule of exponents: (xm)n = xmn.
Change of Base Rule
The base of a logarithm can be changed using this property. It says:
- logb a = (log꜀ a) / (log꜀ b)
Another way of writing this rule is logb a · log꜀ b = log꜀ a.
Using this property, we can change the base to any other number. Hence we can change the base to 10 as well. Then we get: logb a = (log a) / (log b). Thus:
- log2 3 = (log 3) / (log 2)
- log3 2 = (log 2) / (log 3)
Equality Rule of Logarithms
This rule is used while solving the equations involving logarithms. i.e.,
- logb a = logb c ⇒ a = c
It is a kind of canceling log from both sides.
Number Raised to Log Property
When a number is raised to log whose base is same as the number, then the result is just the argument of the logarithm. i.e.,
- aloga x = x
Here are some examples of this property.
- 2log2 5 = 5
- 10log 6 = 6
- eln 3 = 3
Negative Log Property
The negative logs are of the form −logb a. We can calculate this using the power rule of logarithms.
−logb a = logb a-1 = logb (1/a)
Thus,
- −logb a = logb (1/a)
i.e., To convert a negative log into a positive log, we can just take the reciprocal of the argument. Also, to convert a negative log into a positive log, we can take the reciprocal of the base, i.e.,
- −logb a = log1/b a
How to Condense/Expand Logarithms?
We can either compress a group of logs into a single log or expand a single log into a group of logs using the above rules of logs. But the important rules that we use in this process are:
- loga mn = loga m + loga n (Product rule of logarithms)
- loga m/n = loga m - loga n (Quotient rule of logarithms)
- loga mn = n loga m (Power rule of logarithms)
Expanding Logarithms
Let us expand the logarithm log (3x2y3).
log (3x2y3)
= log (3) + log (x2) + log (y3) (By product rule)
= log 3 + 2 log x + 3 log y (By power rule)
Condensing Logarithms
Let us just take the above sum of logarithms and compress it. We should get log (3x2y3) back.
log 3 + 2 log x + 3 log y
= log (3) + log (x2) + log (y3) (By power rule)
= log (3x2y3) (By product rule)
Important Notes on Logarithms:
- The logarithm of 0 is NOT defined as one number raised to another number never gives 0 as the result.
- An exponential equation is converted into a logarithmic equation and vice versa using bx = a ⇔ log b a = x.
- A common log is a logarithm with base 10, i.e., log10 = log.
- A natural log is a logarithm with base e, i.e., loge = ln.
- Logarithms are used to do the most difficult calculations of multiplication and division.
☛ Related Topics:
Solved Examples on Logarithms
-
Example 1: Find the value of log5 (1/25).
Solution:
We will simplify the given expression using the rules of logarithms.
log5 (1/25)
= log5 (1/52)
= log5 (5-2)
= -2 log5 5
= -2(1)
= -2Answer: log5 (1/25) = -2.
-
Example 2: Expand the logarithm log6 \(\left(\frac{6 \mathrm{~m}^{3}}{\sqrt{\mathrm{n}}}\right)\).
Solution:
By using the rules of logs,
log6 \(\left(\frac{6 \mathrm{~m}^{3}}{\sqrt{\mathrm{n}}}\right)\)
= log6 (6m3) - log6 √n
= log6 6 + log6 m3 - log6 n1/2
= 1 + 3 log6 m - (1/2) log6 nAnswer: The expanded form is 1 + 3 log6 m - (1/2) log6 n.
-
Example 3: Compress the following as a single logarithm: 5 log3 x + 2 log3 (4x) - log3 (8x5).
Solution:
By the properties of logarithms,
5 log3 x + 2 log3 (4x) - log3 (8x5)
= log3 x5 + log3 (4x)2 - log3 (8x5)
= log3 x5 + log3 (16x2) - log3 (8x5)
= log3 (x5 · 16x2) - log3 (8x5)
= log3 (16x7) - log3 (8x5)
= log3 (16x7 / 8x5)
= log3 (2x2)Answer: The compressed logarithmic form is log3 (2x2)

FAQs on Logarithms
What are Logs in Math?
Logs are the other way of writing exponent. The formula for conversion between exponential and log forms is: bx = a ⇔ log b a = x. Logarithms are very useful in solving equations involving exponents.
What are the Values of Logarithms log 0, log 1, log 2, log 3, log 4, log 5, log 10, log 100, and log inf?
Here are the values of the given logs:
- log 0 is not defined for any base because a number raised to any number doesn't result in 0.
- log 1 = 0 as 100 = 1
- log 2 ≈ 0.3010 (using calculator)
- log 3 ≈ 0.4771 (using calculator)
- log 4 ≈ 0.6021 (using calculator)
- log 5 ≈ 0.6990 (using calculator)
- log 10 = 1 as 101 = 10
- log 100 = 2 as 102 = 100
- log ∞ = ∞
What is ln in Math?
Ln in math is used to represent the natural logarithms. i.e., ln = "log with base e". For example, e2 = x ⇔ ln x = 2.
What are 3 Types of Logarithms?
There are basically three types of logarithms:
- Common logarithm which is written as log without base. For example: log 2
- Natural logarithm which is written as "ln" (means loge). For example: ln 2
- Logarithm with any other base (no specific name). For example: log3 2.
What are the Values of Logarithms ln e, ln 1, and ln of 0?
Here the values of the given natural logs.
- ln e = 1 as e1 = e
- ln 1 = 0 as e0 = 1
- ln 0 is NOT defined
What are Important Logarithmic Properties?
The important logarithmic properties are:
- Product rule: loga mn = loga m + loga n
- Quotient rule: loga m/n = loga m - loga n
- Power rule: loga mn = n loga m
How do You Calculate Logs?
We can calculate logs using the properties of logarithms. i.e., using the rules of logs we can either compress a set of logarithms into one or expand one logarithm as many. We also use log table and antilog table in calculations.
What is the Derivative of ln x and log x?
Here are the derivatives:
- The derivative of ln x is d/dx (ln x) = 1/x.
- The derivative of log x is d/dx(loga x) (or) (loga x)' = 1/(x ln a).
What is the Integral of ln x and log x?
Here are the given integrals:
- The integral of ln x is ∫ln x dx = x ln x - x + C.
- The integral of log x is ∫log x dx = x log x - x/ln 10 + C.
What is log ln e?
We know that ln e = 1 and log 1 = 0. Using these two facts, log ln e = log 1 = 0.
Is Log Square x Same as 2 Log x?
No, log square x is NOT the same as 2 log x. Observe the following.
- log x square = log x2 = 2 log x (using power rule)
- log square x = log2 x = (log x)2 = (log x) (log x) and this can't be simplified further using any rule.
visual curriculum