Derivative of ln x
In this lesson, we are going to see what is the derivative of ln x. We know that ln x is a natural logarithmic function. It means "ln" is nothing but "logarithm with base e". i.e., ln = logₑ. The derivative of ln x is 1/x. We can prove this in two methods.
- By using the first principle (definition of derivative)
- By using implicit differentiation
Let us see what is the derivative of ln x along with its proof in two methods and a few solved examples.
| 1. | What is the Derivative of ln x? |
| 2. | Derivative of Natural Log by First Principle |
| 3. | Derivative of ln x by Implicit Differentiation |
| 4. | nth Derivative of ln x |
| 5. | FAQs on Derivative of ln x |
What is the Derivative of ln x?
The derivative of ln x is 1/x. i.e., d/dx (ln x) = 1/x. In other words, the derivative of the natural logarithm of x is 1/x. But how to prove this? Before proving the derivative of ln x to be 1/x, let us prove this roughly by using its graph. For this, we graph the function f(x) = ln x first. We know that the derivative of a function at a point is nothing but the slope of the tangent drawn to the graph of the function at that point. We can clearly see that the slope of the tangent drawn
- at x = 1 is 1
- at x = 2 is 1/2
- at x = 3 is 1/3, and so on.
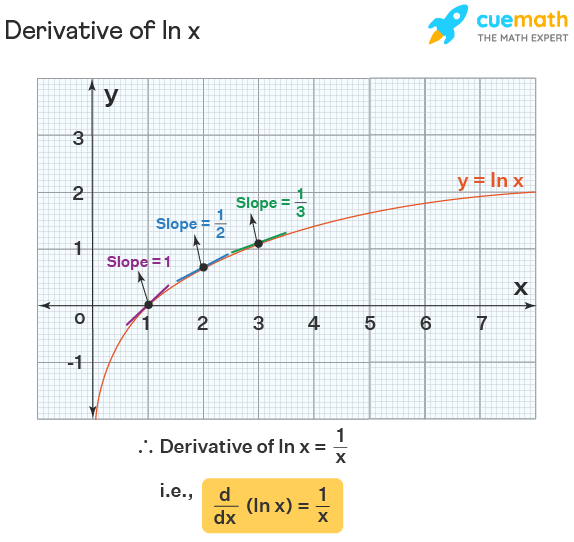
Thus, the derivative of ln x is 1/x which is denoted as d/dx (ln x) = 1/x (or) (ln x)' = 1/x.
ln Derivative Rules
The ln derivative rule says "the derivative of ln x is 1/x". It is mathematically written as follows:
- d/dx (ln x) = 1/x (or)
- (ln x)' = 1/x
Let us prove this formula with various methods.
Derivative of Natural Log by First Principle
Let us prove that the derivative of the natural log is d/dx(ln x) = 1/x using the first principle (the definition of the derivative).
Proof
Let us assume that f(x) = ln x. By the first principle, the derivative of a function f(x) (which is denoted by f'(x)) is given by the limit,
f'(x) = limh→0 [f(x + h) - f(x)] / h
Since f(x) = ln x, we have f(x + h) = ln (x + h).
Substituting these values in the definition of the derivative,
f'(x) = limh→0 [ln (x + h) - ln x] / h
By a property of logarithms, ln m - ln n = ln (m/n). Applying this, we get
f'(x) = limh→0 [ln [(x + h) / x] ] / h
= limh→0 [ln (1 + (h/x))] / h
Let us assume that h/x = t. From this, h = xt.
Also, when h→0, h/x→0, and hence t→0.
Substituting these values in the above limit,
f'(x) = limt→0 [ln (1 + t)] / (xt)
= limt→0 1/(xt) ln (1 + t)
By another property of logarithm, m ln a = ln am. Applying this, we get
f'(x) = limt→0 ln (1 + t)1/(xt)
By a property of exponents, amn = (am)n. Applying this, we get
f'(x) = limt→0 ln [(1 + t)1/t]1/x
Again by applying ln am = m ln a,
f'(x) = limt→0 (1/x) ln [(1 + t)1/t]
Since 'x' is irrespective of the variable of the limit, we can write (1/x) outside of the limit.
f'(x) = (1/x) limt→0 ln [(1 + t)1/t] = (1/x) ln limt→0 [(1 + t)1/t]
Using one of the formulas of limits, limt→0 [(1 + t)1/t] = e. Therefore,
f'(x) = (1/x) ln e = (1/x) (1) = 1/x.
Hence we proved that the derivative of ln x is 1/x using the definition of the derivative.
Differentiation of ln x by Implicit Differentiation
Let us prove that the differentiation of ln x gives d/dx(ln x) = 1/x using implicit differentiation.
Proof
Assume that y = ln x. Converting this into the exponential form, we get ey = x. Now we will take the derivative on both sides of this equation with respect to x. Then we get
d/dx (ey) = d/dx (x)
By using the chain rule,
ey dy/dx = 1
dy/dx = 1/ey
But we have ey = x. Therefore,
dy/dx = 1/x
Thus, we proved the derivative of ln x to be 1/x using implicit differentiation as well.
nth Derivative of ln x
Let us observe the first few derivatives of ln x in order to derive its nth derivative:
- d/dx (ln x) = 1/x
- d2/dx2 (ln x) = d/dx (1/x) = d/dx(x-1) = -1x-2=-1/x2
- d3/dx3 (ln x) = d/dx (-1x-2) = 2x-3 = 2/x3
- d4/dx4 (ln x) = d/dx (2x-3) = -6x-4 = -6/x4
- d5/dx5 (ln x) = d/dx (-6x-4) = 24x-5 = 24/x5
- ...
Here, note that the signs are alternative + and -, and the coefficients are factorials. By using this pattern, it is easy to notice that the nth differentiation of ln x is given by dn/dxn (ln x) = [ (-1)n-1 (n-1)! ]/xn.
Important Notes on Derivative of ln x:
- The derivative of ln x is 1/x.
- Though both log x and ln x are logarithms, their derivatives are NOT the same. i.e.,
d/dx ( ln x) = 1/x
d/dx (log x) = 1/(x ln 10) - We know that the domain of ln x is x > 0 and thus, d/dx (ln |x|) = 1/x as well.
- Derivative of ln(f(x)) using chain rule is 1/(f(x)) · f'(x).
☛ Related Topics:
Examples on Derivative of ln x
-
Example 1: Find the derivative of ln (2x - 3).
Solution:
Let f(x) = ln (2x- 3).
We know that the derivative of natural log is 1/x. Using this and chain rule, we get
f'(x) = 1/(2x - 3) · d/dx (2x - 3)
= 1/(2x - 3) · (2 - 0)
= 2 / (2x - 3).
Answer: The derivative of the given function is 2 / (2x - 3).
-
Example 2: Find the derivative of ln x2.
Solution:
Let f(x) = ln x2.
We can find its derivative in two methods. In each of these methods, we are going to use the fact that "the derivative of ln x is 1/x".
Method 1:
We have ln am = m ln a. So f(x) = 2 ln x.
Its derivative is,
f'(x) = 2 d/dx(ln x) = 2 (1/x) = 2/x
Method 2:
By chain rule,
f'(x) = 1/(x2) d/dx(x2) = (1/x2) · (2x) = 2/x
Answer: The derivative of the given function is 2/x.
-
Example 3: Find the derivative of x ln x.
Solution:
Let f(x) = x ln x = x · ln x = u · v
By product rule,
f'(x) = x d/dx (ln x) + ln x d/dx (x)
Using ln derivative rules, the differentiation of ln x is 1/x and using the power rule, the derivative of x is 1. So
f'(x) = x(1/x) + ln x (1) = 1 + ln x.
Answer: The derivative of the given function is 1 + ln x.

FAQs on Derivative of ln x
What is the Derivative of Natural Log?
The natural logarithm is denoted by "ln". It is nothing but the common logarithm with base "e". The derivative of the natural log of x is 1/x. i.e., d/dx (ln x) = 1/x.
What is the Result of the Differentiation of ln x?
The differentiation of ln x gives 1/x. Mathematically, we can write it as
- d/dx (ln x) = 1/x
- (ln x)' = 1/x
What is the Difference Between the Differentiation of ln x and log x?
It is a common misconception for one to assume that the derivative of ln x and the derivative of log x are equal. But the fact is that their derivatives are NOT equal. We have
- d/dx (log x) = 1/(x ln 10)
- d/dx (ln x) = 1/x
What is the Derivative of 1/x?
To find the derivative of 1/x, we can write it as 1/x = x-1. Then by the power rule, its derivative is -1x-2 (or) -1/x2.
How to Prove that the Derivative of ln x is 1/x?
We can prove that the derivative of ln x is 1/x either by using the definition of the derivative (first principle) or by using implicit differentiation. For detailed proof, click on the following:
What is the Formula for Finding the Derivative of ln x?
The formula of finding the derivative of ln x is, d/dx(ln x) = 1/x. It means that the derivative of ln x is 1/x.
What is nth Derivative of ln x?
The first derivative of ln x is 1/x. The second derivative is -1/x2. Its third derivative is 2/x3. If we continue this process, the nth derivative of ln x is [(-1)n-1 (n-1)!]/xn.
Is the Derivative of ln x the same as the Derivative of log x?
No, the derivative of ln x is NOT the same as the derivative of log x. The derivative of ln x is 1/x whereas the derivative of log x is 1/(x ln 10).
What is the Derivative of (ln x)/x?
To find the derivative of (ln x)/x, we use the quotient rule. Then we get [x (1/x) - ln x (1)]/x2 = [1 - ln x]/x2.
What is the Derivative of ln 3x Using the Derivative of ln x?
By property of logarithms, ln 3x = ln 3 + ln x. By differentiating both sides with respect to x, we get d/dx (ln 3x) = d/dx (ln 3) + d/dx (ln x). We know that ln 3 is a constant and hence its derivative is 0. Thus, d/dx(ln 3x) = 0 + 1/x = 1/x.
visual curriculum