Derivatives

A derivative in calculus is the rate of change of a quantity y with respect to another quantity x. It is also termed the differential coefficient of y with respect to x. Differentiation is the process of finding the derivative of a function.

Let us learn what exactly a derivative means in calculus and how to find it along with rules and examples.

The derivative of a function f(x) is usually represented by d/dx (f(x)) (or) df/dx (or) Df(x) (or) f'(x). Let us see what a derivative technically means. Consider a curve of function f(x) and let two points on it be (x, f(x)) and ((x + h), f(x + h)). Then the slope of the secant line through these points is given by [f(x + h) - f(x)]/(x + h - x) = [f(x + h) - f(x) / h. See the figure below and observe that when the distance between two points is closely equal to 0 (i.e., as h approaches 0), the second point overlaps the original point and the secant line becomes the tangent line. In calculus, the slope of the tangent line is referred to as the derivative of the function. i.e.,

• The derivative of the function, f '(x) = Slope of the tangent = lim_h→0 [f(x + h) - f(x) / h.

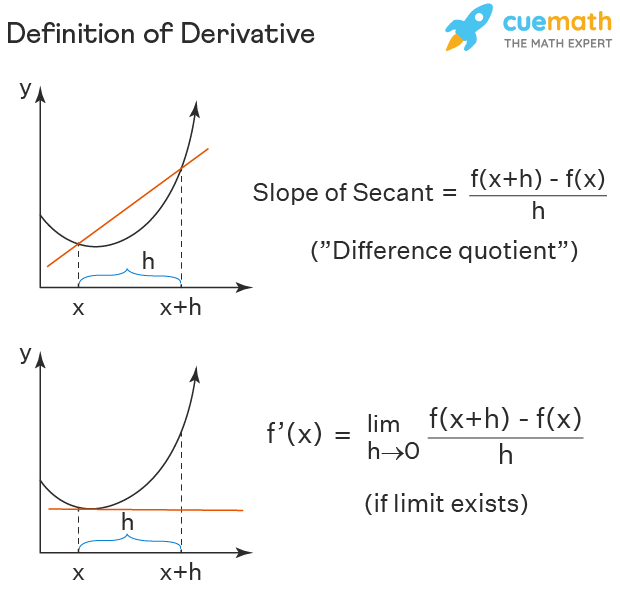
This formula is popularly known as the "limit definition of the derivative" (or) "derivative by using the first principle".

The derivative of a function f(x) in math is denoted by f'(x) and can be contextually interpreted as follows:

• The derivative of a function at a point is the slope of the tangent drawn to that curve at that point.
• It also represents the instantaneous rate of change at a point on the function.
• The velocity of a particle is found by finding the derivative of the displacement function.
• The derivatives are used to optimize (maximize/minimize) a function.
• They are also used to find the intervals where the function is increasing/decreasing as well as the intervals where the function is concave up/down.

Thus, whenever we see the phrases like "slope/gradient", "rate of change", "velocity (given the displacement)", "maximize/minimize" etc then it means that the concept of derivatives is involved.

The derivative of a function can be obtained by the limit definition of derivative which is f'(x) = lim_h→0 [f(x + h) - f(x) / h. This process is known as the differentiation by the first principle. Let f(x) = x² and we will find its derivative using the above derivative formula. Here, f(x + h) = (x + h)² as we have f(x) = x². Then the derivative of f(x) is,

f '(x) = lim_h→0 [(x + h)² - x²] / h
= lim_h→0 [ x² + 2xh + h² - x²] / h
= lim_h→0 [ 2xh + h²] / h
= lim_h→0 [ h(2x + h) ] / h
= lim_h→0 (2x + h)
= 2x + 0
= 2x

Thus, the derivative of x² is 2x. But it may be difficult to use this limit definition to find the derivatives of complex functions. Thus, there are some derivative formulas (of course, which are derived from the above limit definition) that we can use readily in the process of differentiation.

The three basic derivatives of the algebraic, logarithmic / exponential and trigonometric functions are derived from the first principle of differentiation and are used as standard derivative formulas. They are as follows.

Power Rule of Derivatives

By using the above example, the derivative of x² is 2x. Similarly, we can prove that the derivative of x³ is 3x², the derivative of x⁴ is 4x³, and so on. Power rule generalizes this and it is stated as d/dx (xⁿ) = n x^{n - 1}.

Derivatives of Log/Exponential Functions

• The derivative of ln x is, d/dx (ln x) = 1/x
• The derivative of log x is, d/dx (log_a x) = 1/(x ln a)
• The derivative of e^x is, d/dx (e^x) = e^x
• The derivative of a^x is, d/dx (a^x) = a^x ln a

Derivatives of Trigonometric Functions

Here are the derivatives of trigonometric functions.

• If y = sin x, y' = cos x
• If y = cos x, y' = -sin x
• If y = tan x, y' = sec² x
• If y = cot x, y' = -cosec² x
• If y = sec x, y' = sec x tan x
• If y = cosec x, y' = -cosec x cot x

Derivatives of Inverse Trigonometric Functions

Here are the derivatives of inverse trigonometric functions.

• The derivative of inverse sine is, d/dx (sin^-1x) = 1/√(1-x²)
• The derivative of inverse cosine is, d/dx (cos^-1x) = -1/√(1-x²)
• The derivative of inverse tan is, d/dx (tan^-1x) = 1/(1 + x²)
• The derivative of inverse cot is, d/dx (cot^-1x) = -1/(1 + x²)
• The derivative of inverse cosec is, d/dx (csc^-1x) = -1/ [|x| √(x² - 1) ], x ≠ 1, -1, 0
• The derivative of inverse sec is, d/dx (sec^-1x) = 1/ [|x| √(x² - 1) ], x ≠ 1, -1, 0

The following are the fundamental rules of derivatives. Let us discuss them in detail.

Power Rule: By this rule, if y = xⁿ , then dy/dx = n x ^n-1 . Example: d/dx (x⁵) = 5x⁴.

Sum/Difference Rule: The derivative process can be distributed over addition/subtraction. i.e., dy/dx [u ± v]= du/dx ± dv/dx.

Product Rule: The product rule of derivatives states that if a function is a product of two functions, then its derivative is the derivative of the second function multiplied by the first function added to the derivative of the first function multiplied by the second function. dy/dx [u × v] = u · dv/dx + v · du/dx. If y = x⁵ e^x , we have y' = x⁵ . e^x + e^x . 5x⁴ = e^x (x⁵ + 5x⁴)

Quotient Rule: The quotient rule of derivatives states that d/dx (u/v) = (v · du/dx - u · dv/dx)/ v²

Constant multiple Rule: The constant multiple rule of derivatives states that d/dx [c(f(x)] = c · d/dx f(x). i.e., the constant which when multiplied by a function, comes out of the differentiation process. For example, d/dx (5x²) = 5 d/dx (x²) = 5(2x) = 10 x.

Constant Rule: The constant rule of derivatives states that the derivative of any constant is 0. If y = k, where k is a constant, then dy/dx = 0. Suppose y = 4, y' = 0. This rule directly follows from the power rule.

If f and g are differentiable functions in their domain, then f(g(x)) is also differentiable. This is known as the chain rule of differentiation used for composite functions. (fog)'(x) = f'[(g(x)] g'(x). This also can be written as "if y = f(u) and u = g(x) , then dy/dx = dy/du · du/dx.

For example, consider y = tan²x. This is a composite function. We can write this function as y = u², where u = tan x. Then

dy/du = 2u

du/dx = d/dx (tan x) = sec²x

By the chain rule,

dy/dx = dy/du · du/dx

= 2u · sec²x

= 2 tan x sec ² x

In equations where y as a function of x cannot be explicitly defined by the variables x and y, we use implicit differentiation. If f(x, y) = 0, then differentiate on both sides with respect to x and group the terms containing dy/dx at one side, and then solve for dy/dx.

For example, 2x + y = 12

d/dx(2x + y) = d/dx(0)

2 + dy/dx = 0

dy/dx = -2

In a function, we may have the dependent variables x and y which are dependent on the third independent variable. If x = f(t) and y = g(t), then derivative is calculated as dy/dx = f'(x)/g'(x). Suppose, if x = 4 + t² and y = 4t² -5t⁴ , then we find dy/dx as follows.

dx/ dt = 2t and dy/dt = 8t -20t³

dy/dx = (dy/dt)/(dx/dt)

dy/dx = (8t -20t³ )/2t

= 2t (4 - 10t² ) / 2t

dy/dx = 4 - 10t²

We can find the successive derivatives of a function and obtain the higher-order derivatives. If y is a function, then its first derivative is dy/dx. The second derivative is d/dx (dy/dx) which also can be written as d²y/dx². The third derivative is d/dx (d²y/dx²) and is denoted by d³y/dx³ and so on.

Alternatively, the first, second, and third derivatives of f(x) can be written as f'(x), f''(x), and f'''(x). For higher order derivatives, we write the number in brackets as the exponent. Suppose y = 4x³, we get the successive derivatives as follows. y' = 12x² , y'' = 24 x and y''' = 24, y⁽⁴⁾= 0.

If u = f(x,y) we can find the partial derivative of with respect to y by keeping x as the constant or we can find the partial derivative with respect to x by keeping y as the constant. Suppose f(x, y) = x³ y² , the partial derivatives of the function are:

• ∂f/∂x(x³ y²) = 3x²y and
• ∂f/∂y(x³ y²) = x³ 2y

Further, we can find the second-order partial derivatives also like ∂²f/∂x², ∂²f/∂y², ∂²f/∂x ∂y, and ∂²f/∂y ∂x.

Sometimes, the functions are too complex to find the derivatives (or) one function might be raised to another function like y = f(x)^g(x). In such cases, we can take log (or) ln on both sides, apply log rules, and then differentiate on both sides to get dy/dx. This process is known as logarithmic differentiation in calculus.

Example: Find the derivative of y = x^x.

Solution:

Applying ln on both sides,

ln y = ln x^x

ln y = x ln x

Taking derivative on both sides,

1/y dy/dx = x (1/x) + ln x (1) (by chain rule on left side and product rule on right side)

1/y dy/dx = 1 + ln x

dy/dx = y (1 + ln x) = x^x (1 + ln x)

The concept of slope, and hence the derivatives, is used to find the maximum or minimum value of a function. There are two tests that use derivatives and are used to find the maxima/minima of a function. They are

• first derivative test
• second derivative test

First Derivative Test

We can just use the first derivative to determine the maximum or minimum by observing the following points:

• f'(x) represents the slope of a tangent line.
• Hence, if f'(x) > 0, the function is increasing, and if f'(x) < 0, the function is decreasing.
• If f'(x) > 0 is changing to f'(x) < 0 at a point, then the function has a local maximum at that point.
• If f'(x) < 0 is changing to f'(x) > 0 at a point, then the function has a minimum at that point.
• Note that f'(x) = 0 at local maximum and local minimum.

Second Derivative Test

The second derivative test uses the critical points and the second derivative to find the maxima/minima. To perform this test:

• Find the critical points by setting f'(x) = 0.
• Substitute each of these in f''(x). If f''(x) < 0, then the function is maximum at that point and if f''(x)>0, then the function is minimum at that point.
• If f''(x) = 0, the function neither has maxima nor minima at that point, and in this case, it is known as the point of inflection.

Important Notes on Derivatives Calculus:

• A derivative of a function is the rate of change of one quantity over the other.
• Derivative of any continuous function that is differentiable on an interval [a, b] is derived using the first principle of differentiation using the limits.
• If f(x) is given, then its derivative is, f'(x) = lim_h→0 [f(x + h) - f(x) / h.
• Every differentiable function is continuous but the converse may not be true.

☛Related Articles:

• Calculus Calculator
• Derivative Calculator
• Second Derivative Calculator

What are Derivatives in Calculus?

A derivative in calculus is the instantaneous rate of change of a function with respect to another variable. Differentiation is the process of finding the derivative of a function. The derivative of a function is same as the slope of the tangent, rate of change, etc.

Define Derivative.

A derivative of f(x) at x = a is given by f'(x) = lim_h→0 [f(x + h) - f(x)] / h. It is the slope of the tangent to the function f(x). In this formula, [f(x + h) - f(x)] / h is known as the difference quotient.

How Do You Find Derivatives?

The derivatives of functions in math are found using the definition of derivative from the first fundamental principle of differentiation. If f(x) is a given function, its derivative is obtained using f'(x) = lim_h→0 [f(x + h) - f(x)] / h. A lot of rules are derived by using this limit definition which can be directly used to find the derivatives without using the limits.

What are Basic Derivative Formulas?

The basic derivative formulas are, d/dx (xⁿ) = nx^n-1, d/dx (ln x) = 1/x, d/dx (e^x) = e^x, d/dx (a^x) = a^x ln a, d/dx (sin x) = cos x, d/dx (cos x) = - sin x, d/dx (tan x) = sec²x.

Are Calculus Derivatives Hard?

The process of finding the derivatives using a limit definition is a bit hard. To make this easier, we use the rules that are derived by using the formula. As long as we are able to remember the rules, the process of finding derivatives in calculus is so easy just with a little practice.

What Are the Application of Derivatives in Real Life?

There are various applications of derivatives in real life. The rate of change of a function with respect to another quantity is the derivative. To check if a function is increasing or decreasing, to find the equation of the tangent/normal, to find the maximum and minimum values from a graph, to find the displacement-motion problems, to find velocity given displacement, to find the acceleration given displacement and so on.

What is a Derivative Example?

Speed is the instant rate of change of the distance taken by an object at a particular time. The first derivative of the displacement of an object is its velocity. The second derivative of displacement is the object's acceleration. The third derivative of the displacement is the object's jerk and so on.

What is the Difference Between Derivatives and Differentiation in Calculus?

The derivative of a function f(x) at a point is nothing but the slope of the tangent of the function at that point and is found by the limit f'(x) = lim_h→0 [f(x + h) - f(x)] / h. The differentiation is the process of finding the derivatives.