Slope Formula

The slope formula is used to calculate the inclination or steepness of a line. It finds application in determining the slope of any line by finding the ratio of the change in the y-axis to the change in the x-axis. The slope of a line is defined as the change in the "y" coordinate with respect to the change in the "x" coordinate of that line.

What is the Slope Formula?

The slope formula refers to the formula used to calculate the steepness of a line and determines how much it's inclined. To calculate the slope of the lines, the x and y coordinates of the points lying on the line can be used. In other words, it is the ratio of the change in the y-axis to the change in the x-axis.

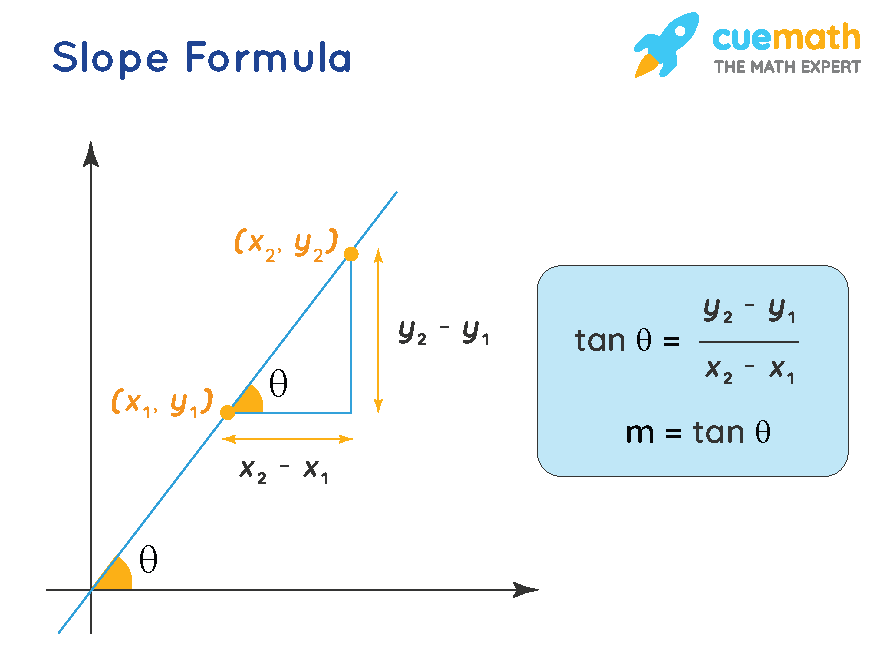
Slope Formula

The formula to calculate slope is given as,

m = (y₂ - y₁)/(x₂ - x₁) = Δy/Δx

where, m is the slope of the line, x₁, x₂ are the coordinates of the x-axis, and y₁, y₂ are the coordinates of the y-axis.

Derivation of Slope Formula

The x and y coordinates of the line are used to calculate the slope of the line. The net change in y coordinate is Δy, while the net change in the x coordinate is Δx. So the change in y coordinate with respect to the change in x coordinate can be written as,

m = Δy/Δx

where

• m is the slope
• Δy is the change in y-coordinates
• Δx is the change in the x-coordinates

We know that tan θ is also the slope of the line where θ is the angle made by the line with the positive direction of the x-axis.

And, tanθ = height/base

Since the height/base between any two given points = (y₂ - y₁)/(x₂ - x₁)

Thus, the slope equation is, m = tanθ = Δy/Δx

From the graph, we observe:

• Δy = (y₂ - y₁)
• Δx = (x₂ - x₁)

Thus, the slope formula is given as: Slope = m = (y₂ - y₁)/(x₂ - x₁)

Slope Equation

As we discussed in the previous section, the slope formula can be used to determine the slope of any line. The equation that can be used in finding this slope can therefore written as,
m = rise/run = tanθ = Δy/Δx = (y₂ - y₁)/(x₂ - x₁)

where,

• m is the slope
• Δy is the change in y-coordinates
• Δx is the change in the x-coordinates
• θ is the angle made by the line with the positive x-axis

Also, the equation of slope of any line using the line equation can be given as,
y = mx + b

where,

• m is the slope of the line
• b is the y-intercept of the line

Let us see the applications of the slope formula in the following solved examples.

Examples Using Slope Formula

Example 1: Find the slope of a line whose coordinates are (2,9) and (4,1)?

Solution:

To find: The slope of the line with coordinates (2,9) and (4,1)

Given, (x₁, y₁) = (2, 9) and (x₂, y₂) = (4, 1)

The slope formula is m = (y₂ - y₁)/(x₂ - x₁)

m = (1 − 9)/(4 − 2)

m = -8/2 = -4

Answer: Slope of the given line = -4

Example 2: Determine the value of b, if the slope of a line passing through the points (b, 7) and (8, -5) is 6.

Solution:

To find: the value of b

Given, Slope = m = 6, Points: (x₁, y₁) = (b, 7) and (x₂, y₂) = (8, -5)
We know that Slope (m) = (y₂ - y₁)/(x₂ - x₁)
6 = (-5-7)/(8-b)
6 = (-12)/(8-b)
-2= (8-b)
-2-8 = -b,
b = 10
Answer: The value of b = 10.

Example 3: If the angle made by a line with the positive y−axis is 30°, then what is the value of the slope of the line?

Solution:

To find: slope of the line

Given: Angle made by a line with the positive y−axis = 30°

We know that if the line makes an angle of 30° from the positive y-axis, then it makes an angle of 120° from the positive x-axis. Therefore, the value of the slope of the line is tan120° = -√3

Answer: The value of the slope of the line = -√3