A day full of math games & activities. Find one near you.

Y Intercept

The y-intercept is the point where the graph intersects the y-axis. To graph, any function that is of the form y = f(x) finding the intercepts is really important. There are two types of intercepts that a function can have. They are the x-intercept and the y-intercept. An intercept of a function is a point where the graph of the function cuts the axis.

Let us understand the meaning of the y-intercept along with its formula and examples.

1.	What is Y-Intercept?
2.	Y-Intercept Formula
3.	Y-Intercept of a Straight Line
4.	How To Find The Y-Intercept?
5.	Y-Intercept of a Quadratic Function (Parabola)
6.	FAQs on Y-Intercept

What is Y Intercept?

The y intercept of a graph is the point where the graph intersects the y-axis. We know that the x-coordinate of any point on the y-axis is 0. So the x-coordinate of a y-intercept is 0.

y intercept definition

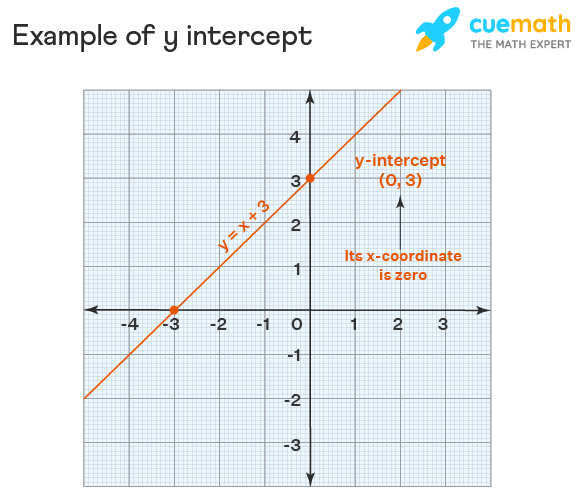
Here is an example of a y-intercept. Consider the line y = x+ 3. This graph meets the y-axis at the point (0,3). Thus (0,3) is the y-intercept of the line y = x+ 3.

y intercept example

Y-Intercept Formula

The y-intercept of a function is a point where its graph would meet the y-axis. The x-coordinate of any point on the y-axis is 0 and we use this fact to derive the formula to find the y-intercept. i.e., the y-intercept of a function is of the form (0, y). Thus, the formula to find the y-intercept is:

y intercept formula

Y Intercept Formula

Here are the steps to find the y intercept of a function y = f(x),

we just substitute x = 0 in it.
solve for y.
represent the y-intercept as the point (0, y).

Here are some examples of y intercepts.

The y-intercept of y = 5x² + 2 is, (0, 2) because when we substitute x = 0, we get y = 5(0)² + 2 = 2.
The y-intercept of y = -5e^x is (0, -5) because when we substitute x = 0, we get y = -5e⁰ = -5.

Y-Intercept of a Straight Line

A straight line can be horizontal or vertical or slanting. The y intercept of a horizontal line with equation y = a is (0, a) and the y intercept of a vertical line does not exist. Let us learn to find the y intercept of a straight line represented in different forms.

Y-Intercept in General Form

The equation of a straight line in general form is ax+by+c=0. For y-intercept, we substitute x=0 and solve it for y.

a(0)+ by + c =0

by + c =0

y = - c/b

Thus, the y-intercept of the equation of a line in general form is:(0, -c/b) or -c/b

y-Intercept in Slope-Intercept Form

The equation of the line in the slope-intercept form is, y=mx+b. By the definition of the slope-intercept form itself, b is the y-intercept of the line. You try by substituting x=0 in y=mx+b and see whether you get b as the y-intercept. Thus, the y-intercept of the equation of a line in the slope-intercept form is (0, b) or b.

y-Intercept in Point-Slope Form

The equation of the line in the point-slope form is, y-y₁=m x-x₁. For y-intercept, we substitute x=0 and solve it for y.

y-y₁ = m (0-x₁ )

y-y₁= - mx₁

y = y₁ - mx₁

Thus, the y-intercept of the equation of a line in the point-slope form is: (0, y₁ - mx₁) or y₁ - mx₁

How To Find Y-Intercept?

We have derived the formulas to find the y-intercept of a line where the equation of the straight line is in different forms. In fact, we do not need to apply any of these formulas to find the y-intercept of a straight line. The y-intercept of the polynomial function of the form y = a₁xⁿ+ a₂ x^n-1+ ... + a_n is just its constant term a_n (or) (0, a_n).

We just substitute x=0 in the equation of the line and solve for y. Then the corresponding y-intercept is y or (0, y).

Equation of Line	Substitute x=0 and solve for y	y intercept
3x+5y -6=0	3(0)+5y-6 =0 5y-6=0 y=6/5	6/5 (or) (0, 6/5)
y= 2x-3	y=2(0)-3=-3	-3 (or) (0, -3)

Equation of Line

Substitute x=0 and solve for y

y intercept

3x+5y -6=0

3(0)+5y-6 =0

5y-6=0

y=6/5

6/5 (or) (0, 6/5)

y= 2x-3

y=2(0)-3=-3

-3 (or) (0, -3)

The y-intercept of a function can be easily found by graphing it using the graphing calculator and locating the point where the graph cuts the y-axis. A function has only one y-intercept because otherwise, it fails the vertical line test. The y-intercept of the second equation of the table (y = 2x - 3) is shown in the graph below.

y intercept of a straight line

Y-Intercept of a Quadratic Function (Parabola)

The procedure for finding the y-intercept of a quadratic function or the y-intercept of a parabola is the same as that of a line (as discussed in the previous section). If a quadratic equation is given, substitute x = 0 and solve for y to get the y intercept.

Examples

Equation of Parabola	Substitute x=0 and solve for y	y-Intercept
y= x²-2x -3	y=0²-2(0)-3=-3	-3 (or) (0, -3)
y= 2x²+5x-3	y=2(0)²+5(0)-3=-3	-3 (or) (0, -3)

y intercept of a parabola

Important Notes on y-Intercept

We substitute x=0 and solve for y to find the y-intercept.
In the same way, we substitute y=0 and solve for x to find the x-intercept.
The lines parallel to the y-axis cannot have y-intercepts as they do not intersect the y-axis anywhere.
The y-intercept of a line is widely used as an initial point while graphing a line by plotting two points.
A function has cannot have more than one y-intercept.

☛ Related Topics:

Examples on Y Intercept

Example 1: Find the y-intercept of the following functions using the formula to find the y-intercept: a) y = x² - 3x + 2 b) y = (x² - 1) / x

Solution:

Using the y-intercept formula, to find the y-intercept of a function, we just substitute x = 0 in it and solve for y.

a) Substitute x = 0 in y = x² - 3x + 2, we get

y = 0² - 3(0) + 2 = 2

So its y-intercept = (0, y) = (0, 2)

b) Substitute x = 0 in y = (x² - 1) / x, we get

y = (0² - 1) / 0 = -1/0 = Not defined

So the given function doesn't have a y-intercept.

Answer: a) (0, 2); b) Does Not Exist
Example 2: If the y-intercept of a function y = a (x - 1) (x - 2) (x - 3) is (0, 12), then find the value of "a".

Solution:

The equation of the given function is:

y = a (x - 1) (x - 2) (x - 3)

Using the y-intercept formula, it can be obtained by substituting x = 0 in it.

y = a (0 - 1) (0 - 2) (0 - 3) = -6a

So the y-intercept is (0, -6a)

But the problem says that the y-intercept of the given function is (0, 12). Thus,

-6a = 12

Dividing both sides by -6,

a = -2

Answer: a = -2
Example 3: If the y-intercept of the function y = 3x² + ax + b is (0, -5) then find the value of 'b'.

Solution:

By using the y intercept formula the y-intercept of the given function is obtained by substituting x = 0

i.e., the y-intercept is, 3(0)² + a (0) + b = b.

But it is given that the y-intercept is, (0, -5) (or) -5.

So, b = -5.

Answer: b = -5.

go to slide go to slide go to slide

Great learning in high school using simple cues

Indulging in rote learning, you are likely to forget concepts. With Cuemath, you will learn visually and be surprised by the outcomes.

Book a Free Trial Class

Practice Questions on y Intercept

go to slide go to slide

FAQs on y Intercept

What is the Meaning of Y Intercept?

The y-intercept of a graph is a point where the graph cuts the y-axis. If the graph is a function, then it has a maximum of one y-intercept.

What is the Slope and Y Intercept of y = 6?

Comparing y=6 with y=mx+b (point-slope form), we get,

the slope, m = 0 and
the y-intercept, b=6

How do you Find the Y-Intercept on the Graphing Calculator?

We use the button "y=" on the calculator to enter the function and then press on the "graph". Then the graph of the function is displayed on the screen. Then press on the "zoom" button. Then press on the "trace" button and enter 0. It will then show the value of y at which x is 0

What is Y Intercept Formula?

The y-intercept formula is used to find the y-intercept of a function. i.e., it is used to find the point where the graph of the function cuts the x-axis. The formula to find y-intercept says that the y-intercept of a function y = f(x) is substituting x = 0 in it and solving for y.

How to Derive Y Intercept Formula?

According to the definition of y-intercept, the y-intercept of a graph is the point where it cuts (or) intersects the y-axis. We know that on the y-axis the x-coordinate is 0. Hence the formula to find the y-intercept of a function y = f(x) is just substituting x = 0 and solving for y.

What are the Applications of Y Intercept Formula?

The y-intercept formula is used to find the y-intercept of a function. The y-intercept is mainly used in the process of graphing a function.

Find the Y Intercept of the Graph Represented by the Equation x = y²+2 y-3.

To find the y-intercept, we substitute x = 0 in the given equation and solve for y. Then,

y²+2y-3 = 0
(y+3)(y-1) = 0
y=-3

y-intercepts are (0, -3) and (0, 1)

How to Use the Y Intercept Formula in Finding the Y Intercept From a Graph?

The y-intercept formula says that the y-intercept of a function y = f(x) is obtained by substituting x = 0 in it. Using this, the y-intercept of a graph is the point on the graph whose x-coordinate is 0. i.e., just look for the point where the graph intersects the y-axis and it is the y-intercept.

Download FREE Study Materials

SHEETS

Math worksheets and
visual curriculum