Straight Line
A straight line is an endless one-dimensional figure that has no width. It is a combination of endless points joined on both sides of a point. A straight line does not have any curve in it. It can be horizontal, vertical, or slanted. If we draw an angle between any two points on the straight line, we will always get a 180-degree. In this mini-lesson, we will explore the world of straight lines by understanding the equations of straight lines in different formats and how to solve the questions based on straight lines.
| 1. | What is a Straight Line? |
| 2. | Types of Straight Lines |
| 3. | Properties of a Straight Line |
| 4. | Equation of a Straight Line |
| 5. | Types of Slope |
| 6. | Frequently Asked Questions(FAQs) |
What is a Straight Line?
A straight line is an infinite length line that does not have any curves on it. A straight line can be formed between two points also but both the ends extend to infinity. A straight line is a figure formed when two points A (x1, y1) and B (x2, y2) are connected with the shortest distance between them, and the line ends are extended to infinity.
In the image shown below, a straight line between two points A and B is shown. A straight line AB is represented by: \(\overleftrightarrow{A B}\)
While straight lines have no definite beginning or end, they are represented in our day-to-day lives with examples such as railway tracks or the freeway.
Types of Straight Lines
Straight lines can be of various types. Generally, the straight lines are classified based on their alignment. Their alignment refers to the angle they form with the x-axis or the y-axis. According to the alignment of straight lines, they are of the following types:
- Horizontal lines
- Vertical lines
- Oblique or Slanted lines
Let us explore them one by one.
Horizontal Lines
The lines which are drawn horizontally and are parallel to the x-axis or perpendicular to the y-axis, are called horizontal lines. They form a 0o or 180o angle with the x-axis and a 90o or 270o angle with the y-axis.
In the given figure, \(\overleftrightarrow{\text{AB}}\) is a horizontal line.
Vertical Lines
The lines which are drawn vertically and are parallel to the y-axis, or perpendicular to the x-axis, are called vertical lines. They form a 90o or 270o angle with the x-axis and a 0o or 180o angle with the y-axis.
In the given figure, \(\overleftrightarrow{\text{CD}}\) is a vertical line.
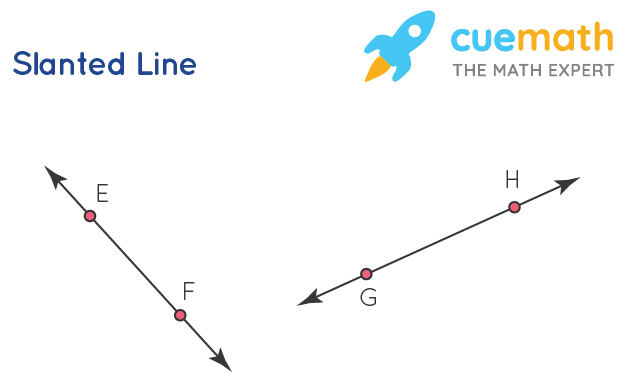
Oblique or Slanted Lines
The lines are drawn in a slanting position or form some angle other than 0o, 90o, 180o, 270o, 360o with the horizontal or vertical lines are called oblique or slanting lines.
In the given figure, \(\overleftrightarrow{\text{EF}}\) and \(\overleftrightarrow{\text{GH}}\) are slanted lines.
Properties of a Straight Line
The properties of straight lines are written below.
- A straight line has infinite length. We can never calculate the distance between the two extreme points of the line.
- A straight line has zero areas, zero volume. but it has infinite length.
- A straight line is a one-dimensional figure.
- An infinite number of lines can pass through a single point, but there is only one unique line that passes through two points.
Equation of a Straight Line
An equation of a straight line is a linear equation. A straight line on a cartesian plane can have different representations based on the known variables, angles, and constants. The slope of a straight line determines the direction of a straight line and tells how steep the line is. It is calculated as the difference in y coordinates/difference in x coordinates, which is also called rise over run. An equation of a straight line is of various forms. They are as follows:
General Equation of a Straight Line
The general equation of a straight line can be given as ax + by + c = 0, where
- a, b, c are constants, and
- x, y are variables.
- The slope is -a/b
Slope and Y-intercept Form
A straight line having slope m = tanθ where θ is the angle formed by the line with the positive x-axis, and y-intercept as b is given by: y = mx + b, where m is the slope.
Slope Point Form
A straight line having slope m = tanθ where θ is the angle formed by the line with the positive x-axis, and passing through a point (x1, y1) is given by: Slope Point Form as y - y1 = m(x - x1)
Two Point Form
A straight line passing through points (x1 , y1) and (x2 , y2) is given by in the two point form as: y - y1 = [(y2 - y1) / (x2 - x1)] (x - x1).
Intercept Form
A straight line having x-intercept as a and y-intercept as b as shown in the figure below where point A is on the x-axis (vertical here) and point B is on the y-axis (horizontal here), is given in the intercept form by x/a + y/b = 1
Equation of Lines Parallel to X-axis or Y-axis
The equation of a line parallel to the x-axis is given by: y = ± a, where
- a is the distance of the line from the x-axis. The value of a is + ve if it lies above the x-axis, and n -ve if it lies below the x-axis.
The equation of a line parallel to the y-axis. is given by: x = ± b, where
- b is the distance of the line from the y-axis. The value of b is +ve if it lies on the right side of the y-axis, and -ve if it lies on the left side of the y-axis.
Below is the image of lines parallel to the x-axis and the y-axis respectively.
Types of Slope
The angle formed by a line with a positive x-axis is the slope of a line. Different lines forms different angles with the x-axis. A line can have slopes varying from positive, negative, 0, or even infinite slope. Let's see some of the cases.
Zero Slope
If a line forms a 0o angle with the x-axis, the slope of the line is 0. The slope of a line is represented by, m = tanθ
Here, θ = 0o . Hence m = tan0 = 0. Therefore, a line with the 0 slope is parallel to the x-axis.
Positive Slope
If a line forms an angle that lies between 0o and 90o with the x-axis, the slope of the line is positive.
Negative Slope
If a line forms an angle that lies between 90o and 180o with the x-axis, the slope of the line is negative.
Infinite Slope
If a line forms a 90o angle with the x-axis, or the line is parallel to the y-axis, the slope of the line is not defined or infinite.
As we know, the slope of a line m = tan θ
Here, θ = 90o . slope m = tan 90o is not defined. Therefore, the line with an infinite slope is parallel to the y-axis.
Important Notes on Straight Line
Here is a list of a few points that should be remembered while studying about a straight line:
- A straight line cannot pass through three non-collinear points.
- If two lines l and m coincide, they follow the relation l = k × m, where k is a real number.
- The acute angle θ between two lines having slopes m1 and m2, where m2 > m1 can be calculated using the formula tanθ =(m2 - m1)/(1 + m2 × m1).
☛Related Topics
Here is a list of related topics to a straight line:
FAQs on Straight Lines
What Do You Understand By Straight Line in Geometry?
A straight line is an endless figure without width. It is a combination of infinite points joined on both ends. It has zero curves or no curve in it. It can be vertical, horizontal, or slanted. In simple words for pre-primary kids, we use a sleeping straight line or standing straight line.
What Do You Use to Draw a Straight Line?
A straight line can be drawn with the help of a ruler, or t- squares, etc. Various geometric tools that have a smooth and flat surface, can also be used to draw a straight line between two points. A straight line that is drawn between two points is known as a line segment. Rulers are the widely used tool to draw a straight line between two points or a straight line in general.
What is the Difference Between Parallel and Perpendicular Straight Lines?
The angle between two parallel lines is 0 degrees, and the angle between two perpendicular lines is 90∘. Parallel lines are aligned in the direction of each other, whereas perpendicular lines are aligned at a 90∘ angle with each other. Slopes of the parallel lines are equal to each other whereas the slopes of perpendicular lines are not equal to each other and the slope of one line is equal to the negative inverse of the other line's slope.
What is the Slope of a Straight Line?
The angle formed by a line with a positive x-axis is the slope of a line, different lines from different angles with the x-axis. A line can have slopes varying from positive, negative, 0, or even infinite slope. The slope of a line is specifically measured with the x-axis or a horizontal line. To measure the slope of any line, we draw a horizontal line from any point on the given line and measure the anti-clockwise angle from the horizontal line to the given line and then calculate the tan θ of the given angle.
What is the General Equation of a Straight Line?
The general equation of a straight line can be given as ax + by + c = 0, where
- a, b, c are constants, and
- x, y are variables.
What is the Angle Between Two Perpendicular Straight Lines?
The angle between the two perpendicular lines is 90 degrees. The two perpendicular lines are aligned in such a way that the product of the slopes of the two lines is equal to -1. Perpendicular lines are seen everywhere, for example, corner of the table, corner of rooms, etc, and we can measure the angle between the sides and find out that the angle between the perpendicular lines is equal to 90 degrees.
What Are the Parallel Straight Lines?
Two lines are said to be parallel lines if they lie in the same plane and never meet. Parallel lines have a 0-degree or 180-degree angle difference from each other. They are aligned in the same direction with each other. If we have two parallel lines where the slope of one line is known to us, then we can equate the slope of the other line equal to the first line, and find out the slope of the other line.