Distance Between Two Lines
Distance between two lines means how far the two lines are located from each other. A line is a figure that is formed when two points are connected with minimum distance between them, and both the ends of a line are extended to infinity. The distance between two lines can be calculated by measuring the perpendicular distance between them. Generally, we find the distance between two parallel lines.
Also, for two non-intersecting lines which are lying in the same plane, the shortest distance between them is the distance that is the shortest of all the distances between two points lying on both lines. Let us learn more about the distance between two lines along with a few solved examples and practice questions.
Distance Between Two Lines
Distance between two lines is measured with reference to two points that are on each of the lines. In a plane, the distance between two straight lines is the minimum distance between any two points lying on the lines. For the distance between two lines, we often deal with different sets of lines such as parallel lines, intersecting lines, or skew lines. So, the distance between two parallel lines is the perpendicular distance from any point on one line to the other line. For two intersecting lines, the shortest distance between such lines eventually comes to zero and the distance between two skew lines is equal to the length of the perpendicular between the lines.
Steps to Calculate The Distance Between Two Lines
- Check whether the given equations of parallel lines are in slope-intercept form (i.e. y= mx + c) or not.
- Also, if the equations of lines are given in the slope-intercept form the slope value should be common for both lines.
- Now find the value of interception point (c1 and c2) and find the value of slope for both the lines.
- Substitute the values in the slope-intercept equation to calculate the value of y.
- In the last, Put all the values in the distance formula discussed below to find the distance between two lines.
Distance Between Two Lines Formula
The formula for distance between two parallel lines is given below:
If we have the slope-intercept form of the two lines as y = mx + c1 and y = mx + c2, then formua for the distance is:
\(d = \frac {|c_2 - c_1|} {\sqrt{1 + m^2}}\)
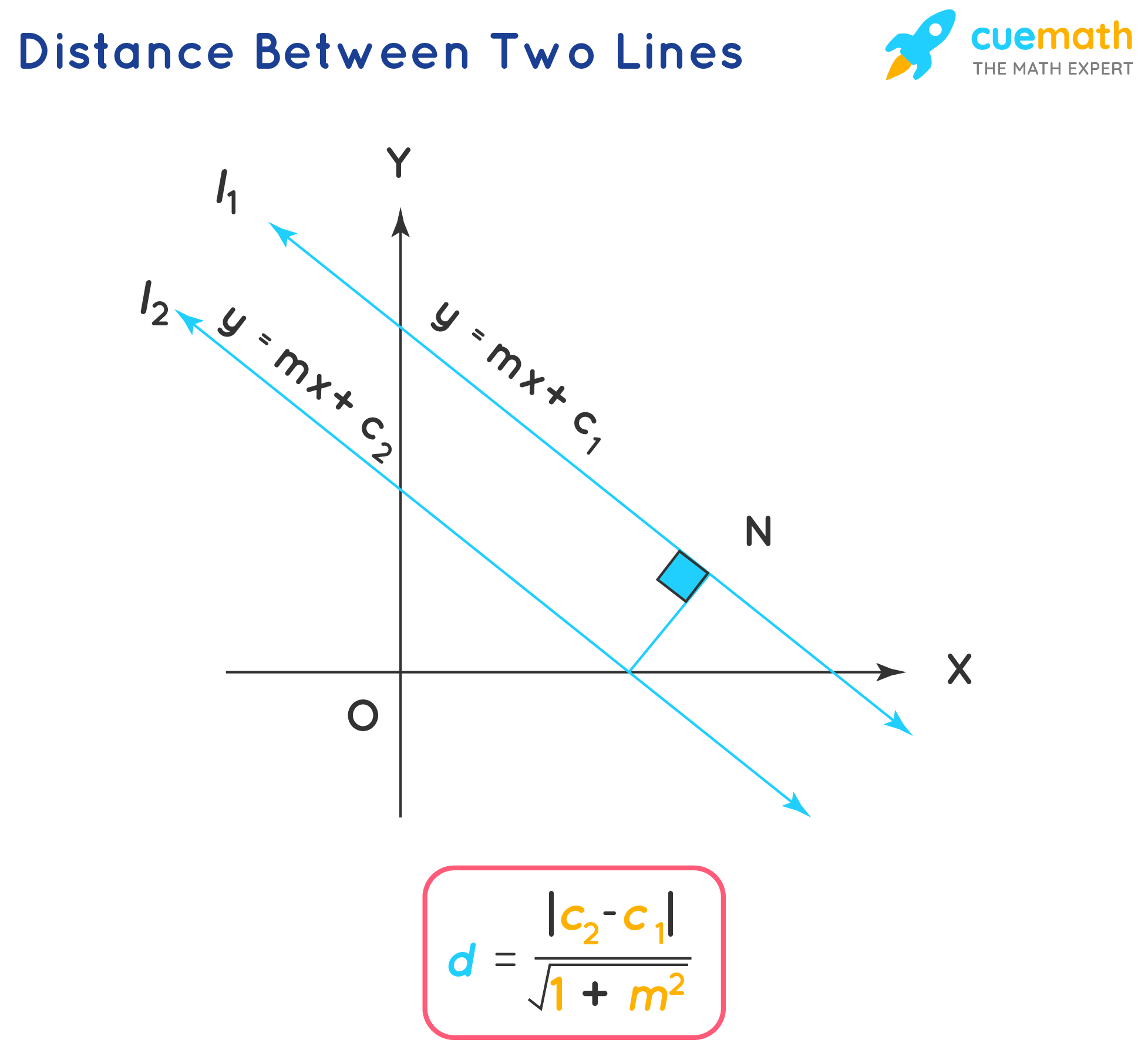
Here, c1 is the constant of line l1 and c2 is the constant for line l2. Also, m represents the slope of the line.
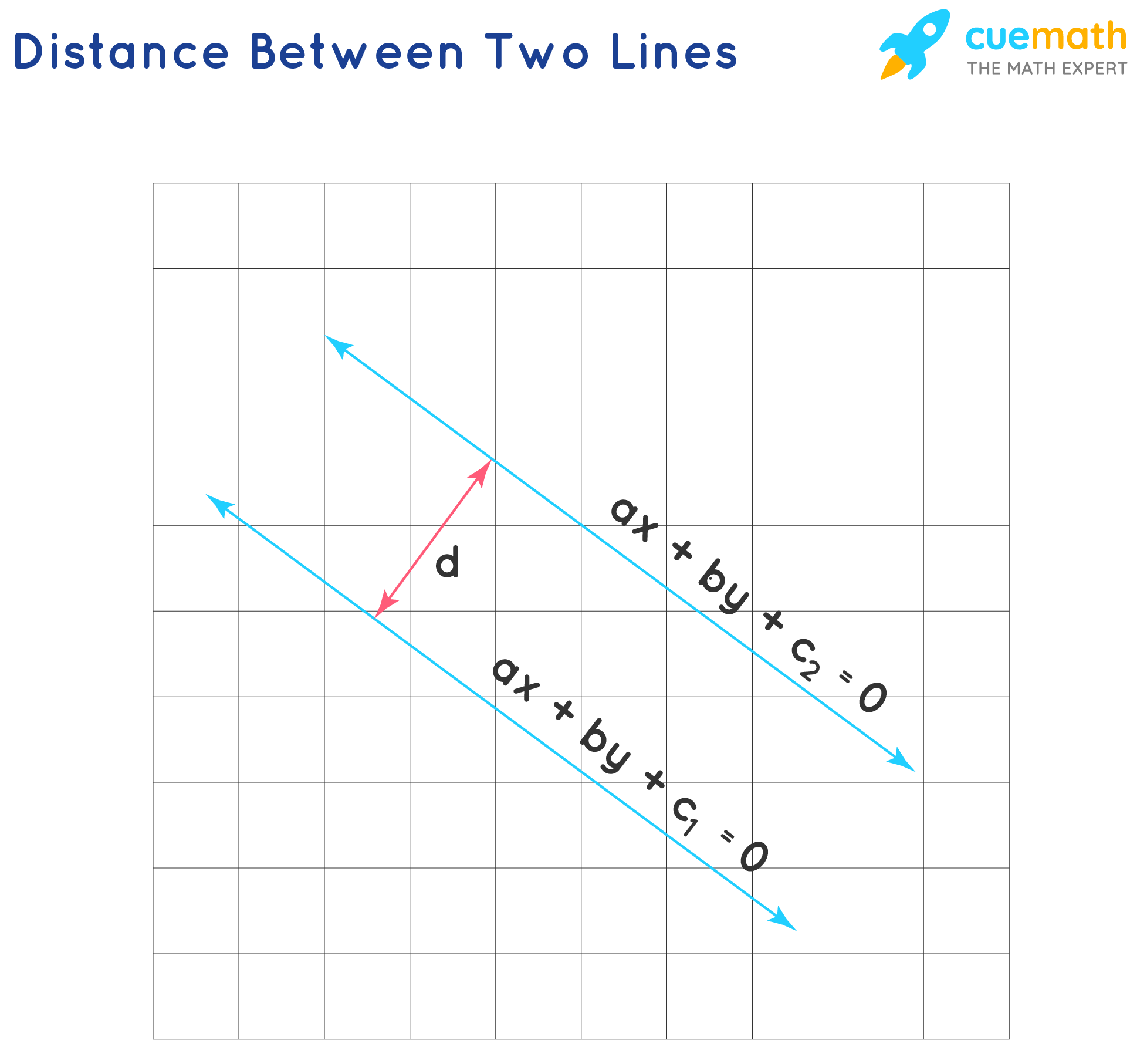
If the equations of the parallel lines are given in the \(ax + by + c_1 = 0 \) and \( ax + by + c_2 = 0\), then the formula for the distance is:
\(d = \dfrac {|c_2 - c_1|} {\sqrt{a^2 + b^2}}\)
Distance Between Two Parallel Lines
In a plane, the distance between two straight lines is the minimum distance between any two points lying on the lines. For the distance between two lines, we often deal with different sets of lines such as parallel lines, intersecting lines, or skew lines. So, the distance between two parallel lines is the perpendicular distance from any point on one line to the other line. For two intersecting lines, the shortest distance between such lines eventually comes to zero and the distance between two skew lines is equal to the length of the perpendicular between the lines.
Let us check the below steps to find the distance between two parallel lines.
- Check whether the given equations of parallel lines are in slope-intercept form (i.e. y= mx + c) or not.
- Also, if the equations of lines are given in the slope-intercept form the slope value should be equal for both lines.
- Now find the value of interception point (c1 and c2) and the value of slope for both the lines.
- Finally, substitute all the values in the distance formula to find the distance between two lines.
The formula for distance between two parallel lines having the slope-intercept form of equations of the two lines as y = mx + c1 and y = mx + c2, is \(d = \frac {|c_2 - c_1|} {\sqrt{1 + m^2}}\). Here, c1 is the constant of line l1 and c2 is the constant for line l2, and m represents the slope of the line. Also if the equations of the parallel lines are given in the form ax + by + c1 = 0 and ax + by + c2 = 0, then the formula for the distance between two parallel lines is \(d = \dfrac {|c_2 - c_1|} {\sqrt{a^2 + b^2}}\).
Shortest Distance Between Two Skew Lines
Before finding the formula to calculate the shortest distance between skew lines, let us recall what are skew lines. Skew lines exist in the multidimensional system, where two lines are non-parallel but never intersects with each other. This is possible only in 3-dimensions or more.
Let us see the formula to calculate the shortest distance between two skew lines whose equations are \( \vec{r_1} = \vec{a_1} + t \vec{b_1} \) and \(\vec{r_2} = \vec{a_2} + t \vec{b_2}\), is:
\(d = |\dfrac{ (\vec{a_2} - \vec{a_1}).(\vec{b_1}\times \vec{b_2})}{(\vec{b_1}\times \vec{b_2})}|\)
The distance between two skew lines, if the equation of the lines is given in cartesian form as \(( x – x_1 ) / a_1 = ( y – y_1 ) / b_1 = ( z – z_1) / c_1 \\ ( x – x_2 ) / a_2 = ( y – y_2 ) / b_2 = ( z – z_2 ) / c_2 \), is:
\(d = \dfrac{\begin{vmatrix} x_2 – x_1 & y_2 – y_1 & z_2 – z_1\\ a_1 & b_1 & c_1\\ a_2 & b_2 & c_2 \end{vmatrix} }{ {[(b_1c_2 – b_2c_1)^2 + ( c_1a_2 – a_2c_1)^2 + (a_1b_2– b_2a_1)^2}]^{1/2}}\)
Let us see a few solved examples on the distance between two lines.
Related topics:
FAQs on Distance Between Two Lines
What is the Formula for Distance Between Two Lines?
The formula for the distance between two lines having the equations y = mx + c1 and y = mx + c2 is: \(d = \frac {|c_2 - c_1|} {\sqrt{1 + m^2}}\). And if the equations of two parallel lines is ax + by + c1 = 0, and ax + by + c2 = 0, then the formula for the distance between the two lines is \(d = \dfrac {|c_2 - c_1|} {\sqrt{a^2 + b^2}}\).
Here,
- c1 is the constant of line l1
- c2 is the constant for line l2
What Happens if Two Lines are Parallel?
If the two lines are parallel, the distance between the two lines will never change. For two parallel lines, the slope of both the lines will be the same but the y-intercept of each line will vary. The shortest distance between the two lines can be calculated if we have the equation of the two lines.
What Is The Distance Between Two Parallel Lines?
The distance between two parallel lines is a constant distance, which do not increase or decrease. The distance between two parallel lines can be calculated from the given equations of the two lines.
How To Find Distance Between Two Parallel Lines?
The distance between two parallel lines can be calculated from the equations of a line. The distance between two parallel lines with the equations y = mx + c1 and y = mx + c2, is \(d = \frac {|c_2 - c_1|} {\sqrt{1 + m^2}}\).
What is the Shortest Distance Between 2 Points?
The shortest distance between the two points is the length of the straight line drawn from one point to the other. The formula for the shortest distance between two points or lines whose coordinate are (x1 y1), and (x2, y2) is: \(\sqrt{(x2-x1)^2+(y2-y1)^2}\). This formula is also known as the distance formula.
How Do You Know Two Lines are Parallel?
To know whether the two lines are parallel or not, we can check the slope of the two lines. If the slope of the two lines is equal then the two lines are parallel. To find out the slope, we convert the given equation of the line into slope-intercept form and compare the two equations to find the value of the slope of the lines.
Do Parallel Lines Mean no Solution?
As the property of parallel lines is that they never intersect each other, other than at infinity, they can not have any solutions. Solutions of parallel lines do not exist, hence it is known that the parallel lines have no solution. And the equations of the parallel lines are known as the inconsistent set of equations.
What are Parallel Lines? Give 2 Examples.
Parallel lines are the lines with the same slope. The distance between the two lines will never change. Some examples of the parallel lines are: 5x + 3y + 6 = 0 and 5x + 3y – 6 = 0 are parallel lines, and y = 5x + 5, and y = 5x - 7 are the parallel lines. We can confirm that the slope of parallel lines given here is the same. i.e., m1 = m2 = 5.