Distance Between Two Points
Distance between two points is the length of the line segment that connects the two given points. Distance between two points in coordinate geometry can be calculated by finding the length of the line segment joining the given coordinates.
Distance between two points in coordinate geometry is calculated by the formula √[(x2 − x1)2 + (y2 − y1)2], where (x1, y1) and (x2, y2) are two points on the coordinate plane. Let us understand the formula to find the distance between two points in a two-dimensional and three-dimensional plane.
What is the Distance Between Two Points?
The distance between any two points is the length of the line segment joining the points. There is only one line passing through two points. So, the distance between two points can be calculated by finding the length of this line segment connecting the two points. For example, if A and B are two points and if \(\overline{AB}\) =10 cm, it means that the distance between A and B is 10 cm.
The distance between two points is the length of the line segment joining them (but this CANNOT be the length of the curve joining them). Note that the distance between two points is always positive.
Distance Between Two Points Formula
The distance between two points using the given coordinates can be calculated by applying the distance formula. For any point given in the 2-D plane, we can apply the 2D distance formula or the Euclidean distance formula given as:
The formula for the distance between two points (d) whose coordinates are (x1,y1) and (x2, y2) is: d = √[(x2 − x1)2 + (y2 − y1)2]
This is also known as the Euclidean Distance Formula.
To find the distance between the points with coordinates (x1,y1, z1) and (x2, y2, z2) given in a 3-D plane, we can apply the 3D distance formula, given as,
d = √[(x2 − x1)2 + (y2 − y1)2 + (z2 − z1)2]
Let's learn how to derive this formula next.
Derivation of Formula for Distance Between Two Points of Coordinates
To derive the formula to calculate the distance between two points in a two-dimensional plane, let us assume that there are two points with the coordinates given as, A(x1, y1) B(x2, y2). Next, we will assume that the line segment joining A and B is \(\overline{AB}\) = d. Now, we will plot the given points on the coordinate plane and join them by a line.
Next, we will construct a right-angled triangle with \(\overline{AB}\) as the hypotenuse.
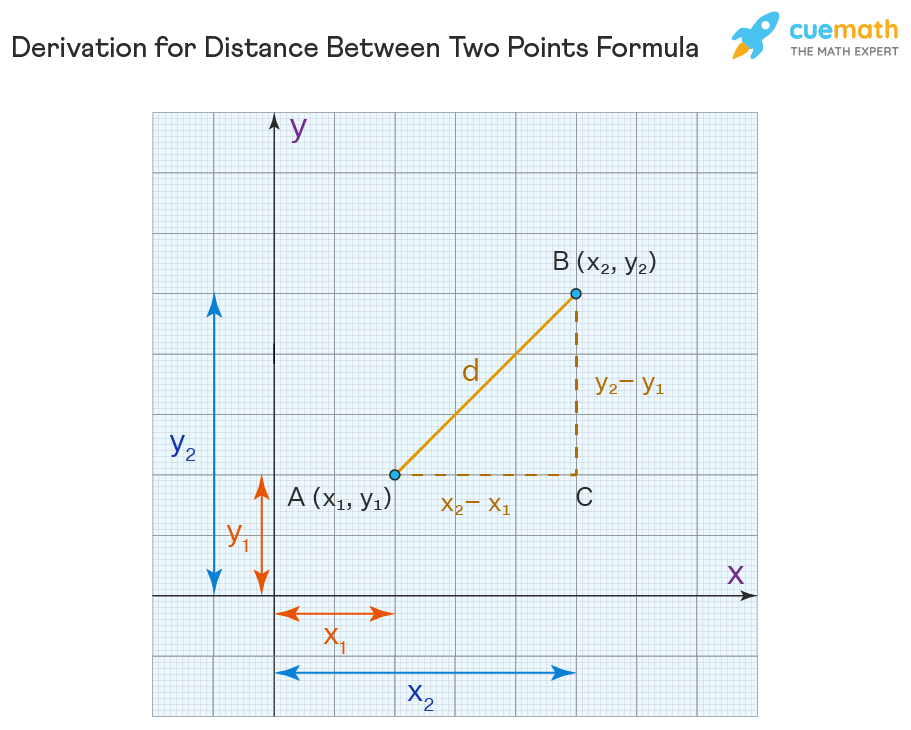
Applying Pythagoras theorem for the △ABC:
AB2 = AC2 + BC2
d2 = (x2 − x1)2 + (y2 − y1)2 (Values from the figure)
Here, the vertical distance between the given points is |y2 − y1|.
The horizontal distance between the given points is |x2 − x1|.
d = √[(x2 − x1)2 + (y2 − y1)2] (Taking square root on both sides)
Thus, the distance formula to find the distance between two points is proved.
Note: In case the two points A and B are on the x-axis, i.e. the coordinates of A and B are (x1, 0) and (x2, 0) respectively, then the distance between two points AB = |x2 − x1|.
Using similar steps and concepts, we can also derive the formula to find the distance between two points given in the 3D plane.
How to Find Distance Between Two Points of Coordinates?
The distance between two points using the given coordinates can be calculated with the help of the following given steps:
- Note down the coordinates of the two given points in the coordinate plane as, A(x1, y1) and B(x2, y2).
- We can apply the distance formula to find the distance between the two points, d = √[(x2 − x1)2 + (y2 − y1)2]
- Express the given answer in units.
Note: We can apply the 3D distance formula in case the two points are given in 3D plane, d = √[(x2 − x1)2 + (y2 − y1)2 + (z2 − z1)2]
Example: Find the distance between the points with coordinates given as, A = (1, 2) and B = (1, 5).
Solution:
The distance between two points using coordinates can be given as, d = √[(x2 − x1)2 + (y2 − y1)2], where (x1, y1) and (x2, y2) are the coordinates of the two points.
⇒ d = √[(1 − 1)2 + (5 − 2)2]
⇒ d = 3 units
From the above example, we can also observe that when the x-coordinates of the given points are the same (i.e. when the points are on a vertical line), we can find the distance between the two points by finding the absolute value of the difference between the y-coordinates.
In the same way, the distance between two points that lie on a horizontal line is the absolute value of the difference in their x-coordinates.
Distance Between Two Points in Complex Plane
The distance between two points in a complex plane is found by using a formula that is similar to the distance between two points formula in cartesian plane. Consider two complex numbers z1 = a + ib and z2 = c + id. Recall the fact that every complex number on a complex plane corresponds to a point on the coordinate plane. Then the distance between the two complex numbers z1 and z2 is:
|z1 − z2| = √[(a − c)2 + (b − d)2]
Here |z1 − z2| is the absolute value of the complex number z1 − z2.
Example: Find the distance between the complex numbers z1 = 1 + 3i and z2 = 2 - 4i.
Solution:
The points that denote the given complex numbers are (1, 3) and (2, -4). So the distance between them is:
|z1 − z2| = √[(1 - 2)2 + (3 + 4)2 = √(1 + 49) = √50 = 5√2 units
☛Related topics:
Important Notes on Distance Between Two Points:
- The distance, d, between two points whose coordinates are (x1,y1) and (x2, y2) is: d = √[(x2 − x1)2 + (y2 − y1)2]
- Note that, there is no harm though we interchange the values x1 and x2 in this formula because (x2 - x1)2 is the same as (x1 - x2)2. The same thing works with y-coordinates as well. Thus, the distance between two points can also be written as √[(x1 − x2)2 + (y1 − y2)2].
- Distance of a point (a, b) from:
(i) x - axis is |b|.
(ii) y - axis is |a|.
We have used the absolute value signs because distance can never be negative.
Examples on Distance Between Two Points
-
Example 2: Show that the points (2, -1), (0, 1) and (2, 3) are the vertices of a right-angled triangle.
Solution:
Let us assume the given points to be:
A = (2, −1)
B = (0, 1)
C = (2, 3)
We will find the length of each side of triangle the distance formula.
AB = √[(0−2)2 + (1−(−1))2]
= √[(−2)2 + (2)2]
= √(4 + 4)
= √8
BC = √[(2 − 0)2 + (3 − 1)2]
= √[(2)2 + (2)2]
= √(4 + 4)
= √8
CA = √[(2 − 2)2 + (3−(−1))2]
= √(02 + 42)
= √16
= 4
Now that we know the lengths of all three sides,
AB2 + BC2 = CA2
(√8)2 + (√8)2 = 42
8 + 8 = 16
16 = 16
Thus, A, B and C satisfy the Pythagoras theorem.
So △ABC is a right-angled triangle.
We can examine the same by marking all the coordinates on a graph:
Answer: The given points form a right-angled triangle.
FAQs on Distance Between Two Points
What is Meant By Distance Between Two Points?
The distance between two points is defined as the length of the straight line connecting these points in the coordinate plane. This distance can never be negative, therefore we take the absolute value while finding the distance between two given points. It is calculated by the formula √[(x2 − x1)2 + (y2 − y1)2].
What is the Distance Formula to Find the Distance Between Two Points in Coordinate Geometry?
In coordinate geometry, the distance between two points formula is given as, d = √[(x2 − x1)2 + (y2 − y1)2], where, (x1, y1), (x2, y2) are the coordinates of the two points. We can apply another formula if the given points liw in 3D plane, d = √[(x2 − x1)2 + (y2 − y1)2 + (z2 − z1)2], where 'd' is the distance between the two points and (x1, y1, z1), (x2, y2, z2) are the coordinates of the two points.
How Do We Calculate the Distance Between Two points in Geometry?
The distance between any two points given in a two-dimensional plane can be calculated using their coordinates. To calculate distance between two coordinates A(x1, y1) and B(x2, y2) we use the formula, d = √[(x2 − x1)2 + (y2 − y1)2].
How to Calculate Distance Between Two Points?
The distance between two points can be calculated using the following steps,
- Denote the given points as (x1, y1) and (x2, y2).
- Apply the Euclidean distance formula, distance, d = √[(x2 − x1)2 + (y2 − y1)2]
- Simplify the square root.
What is the Shortest Distance Between Two Points?
The shortest distance between two points can be calculated by finding the length of the line segment connecting both the points. We can apply the distance formula to find this distance depending on the coordinates given in two or three-dimensional plane.
How to Find the Distance Between Two 2 Using Pythagorean Theorem?
The distance between two points in the cartesian plane can be calculated by applying the Pythagorean theorem.
- We can form a right-angled triangle using the line joining the given two points as the hypotenuse.
- Here the base and perpendicular will be the lines parallel to x and y-axis with one end as one of the given points and the other end as their intersecting point.
- Using the Pythagoras' theorem, (hypotenuse)2 = (base)2 + (perpendicular)2.
- By taking the square root on both sides we can find the length of the hypotenuse with the help of the given coordinates of two points. This length is equal to the distance between two points.
How to Find the Distance Between Two points in 3D Plane?
To calculate the distance between two points in a three-dimensional plane, we can apply the 3D distance formula given as, d = √[(x2 − x1)2 + (y2 − y1)2 + (z2 − z1)2], where 'd' is the distance between the two points and (x1, y1, z1), (x2, y2, z2) are the coordinates of the two points.
How to Derive the Formula to Find The Distance Between Two Points?
We can apply the Pythagoras theorem to derive the distance between two points formula. We can take the line joining the two points as the hypotenuse of a right triangle formed in the cartesian plane. The length of the hypotenuse can be calculated using the Pythagorean theorem and the given coordinates of two points to derive the distance between two points formula.
How to Find the Vertical Distance Between Two Points?
The vertical distance between 2 points can be found by calculating the difference of the y coordinates of the two points, i.e., the vertical distance between two points, dy = |y2 - y1|, where (x1, y1), (x2, y2) are the coordinates of the two points.