Absolute Value
The absolute value of a variable x is represented by |x| which is pronounced as 'Mod x' or 'Modulus of x'. 'Modulus' is a Latin word, which means 'measure'. Absolute value is commonly referred to as numeric value or magnitude. The absolute value represents only the numeric value and does not include the sign of the numeric value. The modulus of any vector quantity is always taken as positive and is its absolute value. Also, quantities like distance, price, volume, and time, are always represented as absolute values.
As an example the absolute value: |+5| = |-5| = 5. There is no sign assigned to absolute value. In this article, we will explore the concept of the absolute value of a number, its symbol, and how to find the absolute value. We will solve various examples based on the concept for a better understanding.
| 1. | What is Absolute Value? |
| 2. | Absolute Value Definition |
| 3. | Absolute Value Sign |
| 4. | Absolute Value of 0 |
| 5. | Absolute Value Function |
| 6. | FAQs on Absolute Value |
What is Absolute Value?
The absolute value of a number is its distance from the origin 0. We know that distance is always a non-negative quantity. Since the absolute value is a distance, the absolute value of a number is always a non-negative number. Sometimes a sign is attributed to a numeric value to signify the direction, in addition to the value. The increase or a decrease of a quantity, values above or below the mean value, profit, or loss in a transaction, is sometimes explained by assigning a positive or negative value to the numeric value. But for absolute value, the sign of the numeric value is ignored and only the numeric value is considered.
Absolute Value Definition
The absolute value of a number is defined as its magnitude irrespective of the sign of the number. To find the absolute value of a real number, we consider only the number and remove the sign. It can only be a non-negative value. The absolute value of a positive number is the number itself, that of a negative number is the number without a negative sign, and the absolute value of 0 is 0.
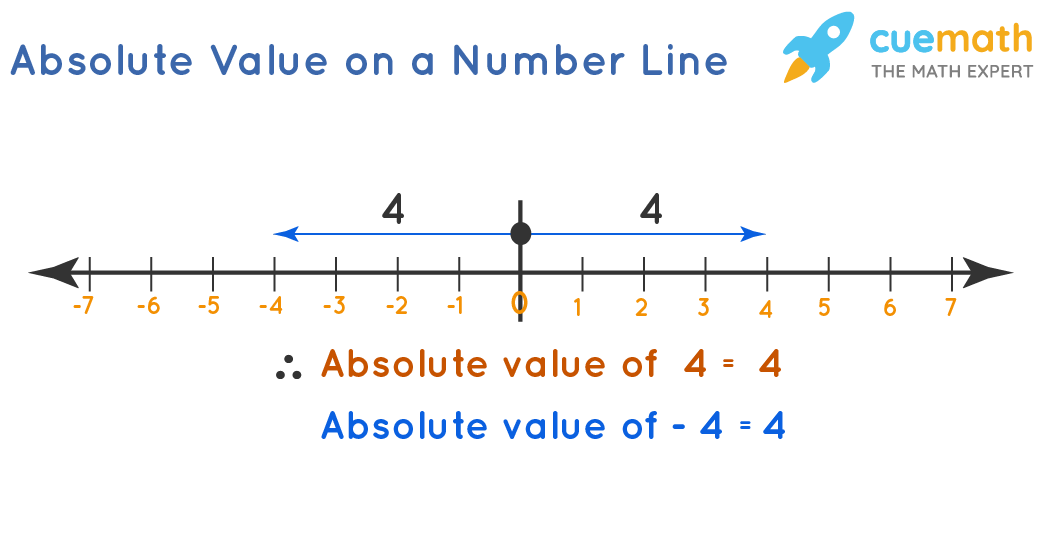
In the above figure, we can observe the absolute values on the number line using the illustration. The absolute value is represented by |x|, and in the above illustration, |4| = |-4| = 4.
Absolute Value Sign
To represent the absolute value of a number (or a variable), we write a vertical bar on either side of the number i.e., |x| where x is an integer. For example, the absolute value of 4 is written as |4|. Also, the absolute value of -4 is written as |-4|. As we discussed earlier, the absolute value results in a non-negative value all the time. Hence, |4|=|-4| =4. That is, it turns negative numbers also into positive numbers. The following figure represents the absolute value symbol.

Absolute Value of a Number
As discussed above, the absolute value of a number is always a non-negative value. To determine the absolute value of a number x, we denote it is |x| and its formula is given by, |x| = x, if x > 0 and |x| = -x, if x < 0, and |x| = 0, if x = 0. Some of the examples of absolute value of a number are:
- |2| = 2
- |-9| = 9
- |3.4| = 3.4
- |-1.23| = 1.23
Absolute Value of 0
So far we have discussed the absolute value of positive and negative numbers. Now, we will discuss the absolute value of zero. Since 0 is neither positive nor positive, therefore the absolute value of 0 is equal to 0. The distance of the number 0 is equal to zero from 0, therefore we can say that the absolute value of 0 is 0.
Absolute Value Function
The absolute value function is defined as f(x) = |x|, { |x| = +x for x ≥ 0, and |x| = -x for x < 0} Using the definition of absolute value, we know that it always results in a non-negative number. Thus, the graph of f(x) = |x| looks as follows.

From the definition of absolute value function, the value of |x| depending on the sign of x. |x|= + x. We also know that √ {x2} = + x. Therefore we have √{x2} = | x |.
Important Notes on Absolute Value
- The absolute value of x is represented by either |x| or abs(x).
- The absolute value of any number always results in a non-negative value.
- We pronounce |x| as 'mod x' or 'modulus of x.'
Think Tank
- We know that absolute value results in a non-negative number. Then why do we have -x in the above definition of Absolute Value Function?
(Hint: What is the sign of -x when x<0 ? Is |-x|= x OR -x when x<0 ?)
Related Articles
Absolute Value Examples
-
Example 1: Mohan wants to find the values of the following. Shall we help her use the definition of absolute value? (I) |-13/5|, (II) - | -3|, (III) |2(-3) + 4|.
Solution:
We know that absolute value results in non-negative values all the time. Thus, we have the following solutions.
(I) | -13/15| = 13/15
(II) - |-3| = -(3) = -3
(III) |2(-3) + 4| = |-6+4| = |-2| = 2
Answer: Therefore(I) | -13/15| = 13/15, (II) - | -3 | = -3, (III) |2(-3) + 4| = 2
-
Example 2: Ria is instructed by her teacher to solve the following absolute value equation using the definition of the absolute function. |x-2| = 4. Can we try to help her?
Solution:
The given equation is |x-2|=4. Using the definition of the absolute value function, when we remove the absolute value sign on one side of the equation. We then get + sign on the other side. x-2= + 4. This results in two equations, which we solve separately.
x - 2 = +4
x = +4 + 2
x = +6
x - 2 = -4
x = -4 + 2
x = -2
Answer: Therefore, the solutions of the given equation are x = 6, x = -2.
-
Example 3: Rohan wants to find the value of -|-x| when x > 0. How can we help Rohan to find the absolute value?
Solution:
Let's help him using the definition of the absolute value function. It is given that x > 0, then we have, -x < 0. Now, by the definition of the absolute value function we have: |-x|= -(-x) = x. Therefore, -|-x| = -x.

FAQs on Absolute Value
What is Absolute Value in Algebra?
The absolute value of a number is defined as its magnitude of the number irrespective of the sign of the number. It gives the distance of a number from the number 0. The absolute value of a number is always a non-negative number.
What is the Absolute Value of -5?
The absolute value of -5 is given by, |-5| = 5 because the absolute value turns negative numbers into positive numbers, i.e., |-5| = 5.
What is Absolute Value Meaning?
The absolute value only gives the numeric value and does not show any sign. The absolute value of |5| is 5, and the absolute value of |-3| is 3.
How Do you Find the Absolute Value of a Negative Number?
The absolute value of a negative number is also a positive value. If a number x < 0, then its absolute value is given by, |x| = -x. For example, |-2| = 2. Irrespective of the sign of the numeric value, the absolute value is always non-negative.
What Is the Use of Absolute Value?
The absolute value is used to inform the numeric value of a quantity, irrespective of the sign of the quantity. Numerous quantities such as length, price, and volume, do not signify any meaning for the sign and are written without any sign. Here the concept of absolute value is helpful to represent such quantities.
What is the Absolute Value of a Negative Integer?
The absolute value of a negative integer is also a positive value. |-5| = 5. For example, the displacement value is sometimes written as -5 meters, but the negative sign only means the direction, and the distance is only 5 meters.
Can the Absolute Value be Negative?
The absolute value is always non-negative. Even for a positive or negative value within the modulus, the absolute value is always positive. |+X| = X, if X > 0.
Can Two Different Numbers have the Same Absolute Value?
Two different numbers can have the same absolute value. For example, the two numbers -7, or +7 have the same absolute value of 7. |-7| = |+7| = 7.
Why is the Absolute Value Always Positive?
Absolute value means the distance of the number from the origin 0. The number represented on a number line can be negative but the absolute value is always positive since the distance is never negative. For example, the absolute value of -9 is 9 which means that the distance from the number -9 to the origin 0 is 9 units on a number line.
What is the One Basic Rule of an Absolute Value?
The basic rule of an absolute value says that the absolute value of any number is always non-negative. If the number is a positive integer, the absolute value of the number is positive, i.e., |15| = 15. If the number is a negative integer, even then, the absolute value is positive, i.e., |-20| = 20.
What is the Absolute Value of 0?
The absolute value of 0 is equal to 0 as the distance of 0 from 0 is equal to 0.
visual curriculum