Parallel and Perpendicular Lines
Parallel and perpendicular lines are an important part of geometry and they have distinct characteristics that help to identify them easily. Two lines are termed as parallel if they lie in the same plane, are the same distance apart, and never meet each other. Perpendicular lines are intersecting lines that always meet at an angle of 90°. Let us learn more about parallel and perpendicular lines in this article.
| 1. | What are Parallel and Perpendicular Lines? |
| 2. | Difference Between Parallel and Perpendicular Lines |
| 3.. | Equations of Parallel and Perpendicular Lines |
| 4. | FAQs on Parallel and Perpendicular Lines |
What are Parallel and Perpendicular Lines?
If two straight lines lie in the same plane, and if they never intersect each other, they are called parallel lines. They are always the same distance apart and are equidistant lines. The symbol || is used to represent parallel lines. For example, AB || CD means line AB is parallel to line CD. On the other hand, when two lines intersect each other at an angle of 90°, they are known as perpendicular lines. Perpendicular lines are denoted by the symbol ⊥. For example, PQ ⊥ RS means line PQ is perpendicular to line RS. Observe the following figure and the properties of parallel and perpendicular lines to identify them and differentiate between them.
Properties of Parallel Lines
- Parallel lines are always equidistant from each other.
- They never meet at any common point.
- They lie in the same plane.
Properties of Perpendicular Lines
- Perpendicular lines always intersect at 90°.
- All perpendicular lines can be termed as intersecting lines, but all intersecting lines cannot be called perpendicular because they need to intersect at right angles.
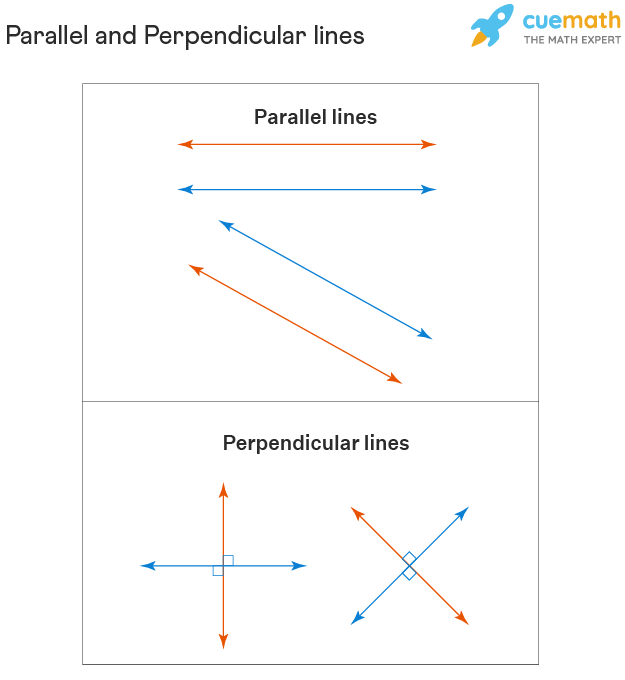
Difference Between Parallel and Perpendicular Lines
Although parallel and perpendicular lines are the two basic and most commonly used lines in geometry, they are quite different from each other. The following table shows the difference between parallel and perpendicular lines.
| Parallel Lines | Perpendicular Lines |
|---|---|
| Parallel lines are those that never intersect and are always the same distance apart. | Perpendicular lines are those that always intersect each other at right angles. |
| Perpendicular lines are denoted by the symbol ⊥ | The symbol || is used to represent parallel lines. |
| Examples of parallel lines: Railway tracks, opposite sides of a whiteboard. | Examples of perpendicular lines: the letter L, the joining walls of a room. |
Equations of Parallel and Perpendicular Lines
The equation of a straight line is represented as y = ax + b which defines the slope and the y-intercept. Here 'a' represents the slope of the line. Since two parallel lines never intersect each other and they have the same steepness, their slopes are always equal. For example, if the equations of two lines are given as, y = -3x + 6 and y = -3x - 4, we can see that the slope of both the lines is the same (-3). Therefore, they are parallel lines. Mathematically, this can be expressed as m1 = m2, where m1 and m2 are the slopes of two lines that are parallel.
Perpendicular lines do not have the same slope. The slope of one line is the negative reciprocal of the other line. This can be expressed mathematically as m1 × m2 = -1, where m1 and m2 are the slopes of two lines that are perpendicular. For example, if the equations of two lines are given as: y = 1/4x + 3 and y = - 4x + 2, we can see that the slope of one line is the negative reciprocal of the other. Therefore, they are perpendicular lines. In this case, the negative reciprocal of -4 is 1/4 and vice versa. Negative reciprocal means, if m1 and m2 are negative reciprocals of each other, their product will be -1.
Hence, it can be said that if the slope of two lines is the same, they are identified as parallel lines, whereas, if the slope of two given lines are negative reciprocals of each other, they are identified as perpendicular lines.
☛ Related Articles
Check out the following pages related to parallel and perpendicular lines.
Parallel and Perpendicular Lines Examples
-
Example 1: Observe the blue highlighted lines in the following examples and identify them as parallel or perpendicular lines.
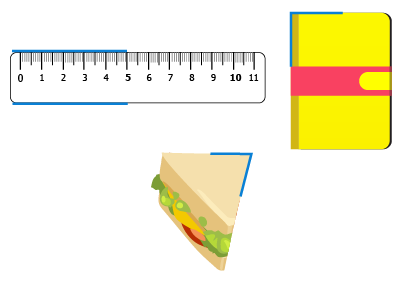
Solution: We need to know the properties of parallel and perpendicular lines to identify them.
a.) Ruler: The highlighted lines in the scale (ruler) do not intersect or meet each other directly, and are the same distance apart, therefore, they are parallel lines.
b.) Sandwich: The highlighted lines in the sandwich are neither parallel nor perpendicular lines. They are not parallel because they are intersecting each other. They are not perpendicular because they are not intersecting at 90°.
c.) Book: The two highlighted lines meet each other at 90°, therefore, they are perpendicular lines.
FAQs on Parallel and Perpendicular Lines
What are Parallel and Perpendicular Lines?
Parallel lines are those lines that do not intersect at all and are always the same distance apart. Perpendicular lines are those lines that always intersect each other at right angles.
What Letters have Parallel and Perpendicular Lines?
There are some letters in the English alphabet that have parallel and perpendicular lines in them. Observe the horizontal lines in E and Z and the vertical lines in H, M and N to notice the parallel lines. Similarly, observe the intersecting lines in the letters L and T that have perpendicular lines in them.
What Shape has Parallel and Perpendicular Lines?
There are many shapes around us that have parallel and perpendicular lines in them. For example, the opposite sides of a square and a rectangle have parallel lines in them, and the adjacent lines in the same shapes are perpendicular lines. If we see a few real-world examples, we can notice parallel lines in them, like the opposite sides of a notebook or a laptop, represent parallel lines, and the intersecting sides of a notebook represent perpendicular lines.
How many Parallel and Perpendicular lines are there in a Square?
In a square, there are two pairs of parallel lines and four pairs of perpendicular lines. The opposite sides are parallel and the intersecting lines are perpendicular.
What Letter has both Parallel and Perpendicular Lines?
There are some letters in the English alphabet that have both parallel and perpendicular lines. For example, the letter H, in which the vertical lines are parallel and the horizontal line is perpendicular to both the vertical lines. Similarly, in the letter E, the horizontal lines are parallel, while the single vertical line is perpendicular to all the three horizontal lines.
How to Identify Parallel and Perpendicular Lines?
Parallel and perpendicular lines can be identified on the basis of the following properties:
Properties of Parallel Lines:
- Parallel lines are coplanar lines.
- They are always equidistant from each other.
- They do not meet at any common point.
Properties of Perpendicular Lines:
- Perpendicular lines always intersect at right angles.
- All perpendicular lines can be termed as intersecting lines, but all intersecting lines cannot be called perpendicular because they need to intersect at right angles.
What are the Slopes of Parallel and Perpendicular Lines?
If the slope of two given lines is equal, they are considered to be parallel lines. For example, if the equation of two lines is given as, y = 4x + 3 and y = 4x - 5, we can see that their slope is equal (4). These lines can be identified as parallel lines. Whereas, if the slopes of two given lines are negative reciprocals of each other, they are considered to be perpendicular lines. For example, if the equation of two lines is given as, y = 1/5x + 3 and y = - 5x + 2, we can see that the slope of one line is the negative reciprocal of the other. In this case, the negative reciprocal of 1/5 is -5. Therefore, these lines can be identified as perpendicular lines.
How are Parallel and Perpendicular Lines Similar?
Parallel and perpendicular lines have one common characteristic between them. They both consist of straight lines.