Points and Lines
In geometry, a point is a location represented by a dot. A point does not have any length, width, shape or size, it only has a position. When two distinct points are connected they form a line.
| 1. | What is a Point and a Line? |
| 2. | Types of Points and Lines |
| 3. | Tips on Points and Lines |
| 4. | Solved Examples |
| 5. | Practice Questions |
| 6. | FAQs on Points and Lines |
What is a Point and a Line?
The concept of points and lines is important to understand geometry figures. With the help of points, we can label and identify the geometry figures and with the help of lines, we can draw the figures.
Point
A point is defined as a location in any space and is represented by a dot (.). It does not have any length, height, shape, or size. It marks the beginning to draw any figure or shape and is labeled with capital letters.
Line
A series of points connected by a straight path is defined as a line. A line is usually defined by two points. It can be marked with a single letter in the lower case or by two capital letters. A line has no thickness and can extend indefinitely in both directions. The length of a line is undefined and it can have infinite numbers of points. Observe the following figure to know the difference between a point and a line.

Types of Points and Lines
There are different types of points in geometry. Let us discuss them to identify them easily.
Collinear Points and Non-Collinear Points
If three or more points lie on a single straight line then the points are called collinear points. If the group of points do not lie on the same line then those points are called non-collinear points.
Coplanar Points and Non-Coplanar Points
If a group of points lie on the same plane then they are said to be coplanar points. A set of points that do not lie on the same plane are non-coplanar points.
Observe the following figure which shows the different types of points.

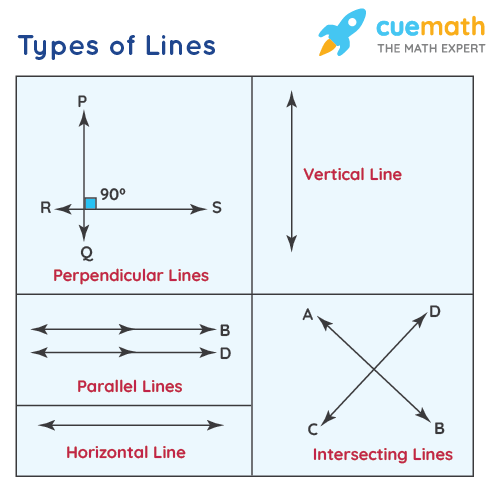
Types of Lines
Just like the different types of points, there are different types of lines which can be distinguished easily on the basis of their unique properties.
- Horizontal Line – A line that is mapped from left-to-right or right-to-left and is parallel to the x-axis in a plane is called a horizontal line.
- Vertical Line – A line that is mapped from up to down or down to up and is parallel to the y-axis in a plane is called a vertical line.
- Intersecting Lines – When two lines cross each other and meet at a point, they are known as intersecting lines. The point at which they meet is known as the point of intersection.
- Perpendicular Lines– When two lines intersect exactly at 90°, they are known as perpendicular lines.
- Parallel Lines – Two lines are said to be parallel if they do not intersect at any point and are equidistant.
Observe the figure given below which shows the different types of lines.
Tips on Points and Lines
- A point does not have a length, width, shape or size.
- When two distinct points are connected they make a line.
- A line extends in both directions infinitely.
- Parallel lines do not intersect each other.
- The lines that intersect each other at 90° are known as perpendicular lines.
- Two or more points that lie on a single straight line are collinear points.
- Two or more points that lie on the same plane are coplanar points.
Related Articles on Points and Lines
Check out these interesting articles to know more about points and lines.
Solved Examples
-
Example 1: Identify the collinear points and non-collinear points in the figure given below.

Solution: The points A, B, C lie on the same straight line, therefore, they are collinear points. Points D and E do not lie on the same line and so they are non-collinear points.
-
Example 2: Identify the different types of lines in the figure given below.

Solution: In the given figure:
- AB and CD are horizontal lines since they move from left to right.
- XY is a vertical line since it moves from top to bottom.
- AB and CD are parallel lines since they do not meet and intersect at any point.
- Lines XY and AB are intersecting lines that intersect at point O.
- Line XY is perpendicular to AB since they intersect each other at 90°.
-
Example 3: Find the set of coplanar and non-coplanar points from the figure.

Solution: Points A, B and C lie on the same plane and so they are coplanar points, but D is non-coplanar with respect to A, B and C since point D lies outside the given plane.

FAQs on Points and Lines
How many Points are Required to Determine a Line?
A line is identified and determined by two points which are joined to form the line. That is the reason why a line is usually named by two capital letters.
How Many End-Points are there in a Line?
A line does not have an end-point as it can extend infinitely in both directions.
What do we Call Points that do not lie on the Same Line?
The points that do not lie on the same line are called non-collinear points.
What are the Real-Life Examples of Points and Lines?
A few real-life examples of points are a pencil tip, the tip of a needle, or the location of a place on a map. A few real-life examples of lines are a wire or the edge of a table.
What are the Types of lines in Geometry?
There are different types of lines in geometry that can be identified on the basis of their properties, like, horizontal lines, vertical lines, parallel lines, perpendicular lines, and intersecting lines.
visual curriculum