Lines and Angles - Basic Terms
In geometry, lines and angles are the basic terms that set up the foundation for the subject. A line is defined as a row of closely spaced dots that extends infinitely in two directions. It has only one dimension, that is its length. A horizontal mark drawn on a piece of paper can be considered as an example of a line. An angle is defined as a figure created by two rays that meet at a common endpoint. They are measured in degrees, using a protractor. All geometry shapes have lines and angles in them. Let us learn more about the various types of lines and angles in this lesson.
| 1. | Definition of Lines and Angles |
| 2. | Types of Lines and Angles |
| 3. | Properties of Lines and Angles |
| 4. | FAQs on Lines and Angles - Basic Terms |
Definition of Lines and Angles
The concept of lines was introduced by the ancient mathematicians to represent straight objects that did not have any width or depth. While lines are simpler to understand, an angle is a shape that is formed by the intersection of two line segments, lines, or rays. When two rays intersect each other in the same plane, they form an angle.
Lines
A line is a one-dimensional figure that extends in both directions infinitely without any width. It is made up of infinite number of points close to each other. Euclid denotes the line as a breadthless length. In a cartesian plane, it is denoted by the linear equation ax + by = c. Observe the line shown in the figure given below.

Rays
Rays are the lines with one end as the start point and the other end going to infinity. They extend in one direction without ending. When two rays are joined end to end, they form an angle.They are represented as \( \overrightarrow{\mathrm{PQ}}\)

Line Segment
When a line has two endpoints, it is known as a line segment. The length of a line segment can be measured and it is written as \(\overline{AB}\)

Angles
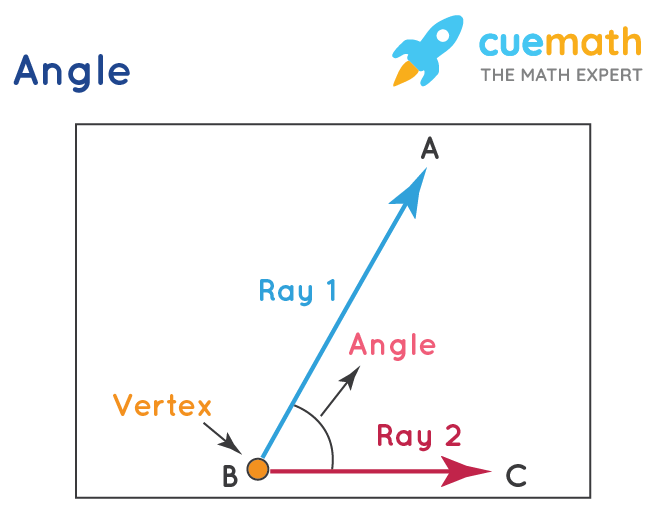
Types of Lines and Angles
There are different types of lines and angles in geometry. First, let us read about the different types of lines.
Types of Lines
Lines can be classified into different types depending upon their properties. The table below shows the different types of lines.
| Type of Lines | Description | Illustration |
| Horizontal Line |
These lines are parallel to the x-axis and perpendicular to the y-axis |
|
| Vertical Line | These lines are parallel to the y-axis and perpendicular to the x-axis |
|
| Parallel Lines | When two straight lines move alongside and maintain a constant distance between each other up to infinity, they are known as parallel lines. The symbol || is used to represent parallel lines. |
|
| Perpendicular Lines | When two lines intersect each other at an angle of 90°, they are known as perpendicular lines. Perpendicular lines are denoted by the symbol of ⊥ |
|
| Transversal Lines | When a line intersects two lines at different respective points, then it is known as a transversal line. |
|
Types of Angles
Angles can be categorized into different types based on their measurements. Angles are generally of 6 types:
- Acute angle: If the measure of an angle is less than 90∘ then it is known as an acute angle.
- Obtuse angle: If the measure of an angle is greater than 90∘ but less than 180∘, then it is known as an obtuse angle.
- Right angle: If the measure of an angle is exactly equal to 90∘ then it is known as a right angle.
- Straight angle: If the measure of an angle is 180∘ then it is known as a straight angle.
- Reflex angle: If the measure of an angle is greater than 180∘ but less than 360∘, then it is known as a reflex angle.
- Complete angle: If the measure of an angle is 360∘ then it is known as a complete angle.
The table given below shows the different types of angles that are categorized based on their measurements.
| Type of Angles | Measurements | Illustration |
|---|---|---|
|
Acute Angle |
Here, (∠ABC = 40∘) < 90∘ |
|
|
Right Angle |
Here, ∠ABC = 90∘ |
|
|
Obtuse Angle |
Here, 90∘ < (∠ABC = 117∘) <180∘ |
|
|
Straight Angle |
Here, ∠AOB = 180∘ |
|
|
Reflex Angle |
180∘ < (Reflex Angle = 330∘) < 360∘ |
|
|
Complete Angle |
Angle = 360∘ |
|
Properties of Lines and Angles
As we have seen that there are different kinds of lines and angles, each of them has different specific properties. However, there are some basic common properties of lines and angles that can be discussed.
Properties of Lines
- Lines can be defined as a set of an infinite number of points close to each other.
- They extend infinitely in both directions.
- They are one-dimensional and do not have any depth or thickness.
Properties of Angles
- An angle is a geometrical figure that is formed when two lines intersect each other in the same plane.
- The lines that form an angle are termed as its arms (sides), and the point at which they form the angle is called its vertex.
Tips on Lines and Angles
Here is a list of a few tips that should be remembered while studying lines and angles:
- All geometry shapes have angles and lines in them.
- A line is a one-dimensional figure, with no breadth, and that extends in both directions infinitely.
- These are the lines with one end as the start point and the other end going to infinity. These are used to form angles.
- Angles are formed when two rays intersect at a point.
Related Topics
Check out these interesting articles to learn more about the properties of lines and angles, and their related topics.
Examples on Lines and Angles
-
Example 1: If the measure of ∠AOB is 57°. Find the measure of the angle which is the reflex angle of this angle.
Solution:
According to the properties of lines and angles, we know that the sum of an angle and its reflex angle is 360°.
Therefore,
∠AOB + Reflex ∠AOB = 360°
Reflex ∠ AOB = 360° − 57°
Reflex ∠AOB = 303°

Answer: The reflex ∠ AOB is 303°.
-
Example 2: Find the value of x in the given figure if AOB is a line, ∠AOC = 4x, and ∠BOC = 2x.

Solution:
One of the properties of lines and angles states that the sum of the adjacent linear angles formed by a line is 180°.
Therefore, 4x + 2x = 180°
6x = 180°
x = 180°/6 = 30°
We get the value of x as 30°. Hence, the first angle AOB is 4x = 4 × 30 = 120°. The other angle COB is 2x = 2 × 30 = 60°
Answer: x = 30°.

FAQs on Lines and Angles
What are Lines and Angles in Geometry?
A line is defined as a row of closely spaced dots that extends infinitely in two directions. It has only one dimension, that is its length. An angle is a shape that is formed by the intersection of two line segments, lines, or rays. In other words, when two rays, lines, or line segments intersect each other in the same plane, they form an angle.
What are the Different Types of Lines and Angles?
There are different types of lines and angles in geometry. The six types of angles are right angle, acute angle, obtuse angle, straight angle, reflex angle, and complete angle. The different types of lines are horizontal lines, vertical lines, parallel lines, perpendicular lines, and transversal lines.
What are the Properties of Lines and Angles?
Since there are different kinds of lines and angles, each of them has different properties. However, there are some common properties of lines and angles that can be listed.
Properties of Lines
- Lines can be defined as a set of an endless number of points close to each other.
- They extend infinitely in both directions.
- They are one-dimensional and do not have any depth or thickness.
Properties of Angles
- An angle is a geometrical figure that is formed when two lines intersect each other in the same plane.
- The lines that form an angle are termed as its arms (sides) and the point at which they form the angle is called its vertex.
What are Perpendicular Lines?
When two lines intersect each other at an angle of 90°, they are known as perpendicular lines. Perpendicular lines are denoted by the symbol of ⊥.
What are Horizontal and Vertical Lines?
Horizontal lines are the lines that are parallel to the x-axis and perpendicular to the y-axis. Vertical Lines are the lines that are parallel to the y-axis and perpendicular to the x-axis.
How are Straight Lines Classified?
Straight lines are classified into horizontal and vertical lines. Apart from these, there are other types of lines such as parallel lines, transversal lines, and perpendicular lines.
Is it True that the Linear Pair of Angles are Always Congruent?
It is false. Linear pairs of angles are not always congruent. Only when the measure of each of the angles is 90°, a linear pair of angles is considered to be congruent. Linear pairs of angles are always supplementary.
visual curriculum










