Plane Definition
In mathematics, a plane is a flat, two-dimensional surface that extends up to infinity. Planes can appear as subspaces of some multidimensional space, as in the case of one of the walls of the room, infinitely expanded, or they can enjoy an independent existence on their own, as in the setting of Euclidean geometry. The two types of planes are parallel planes and intersecting planes. Two non-intersecting planes are called parallel planes, and planes that intersect along a line are called Intersecting planes.
Definition of a Plane
In geometry, a plane is a flat surface that extends into infinity. It is also known as a two-dimensional surface. A plane has zero thickness, zero curvature, infinite width, and infinite length. It is actually difficult to imagine a plane in real life; all the flat surfaces of a cube or cuboid, flat surface of paper are all real examples of a geometric plane. We can see an example of a plane in which the position of any given point on the plane is determined using an ordered pair of numbers or coordinates. The coordinates show the correct location of the points on the plane.
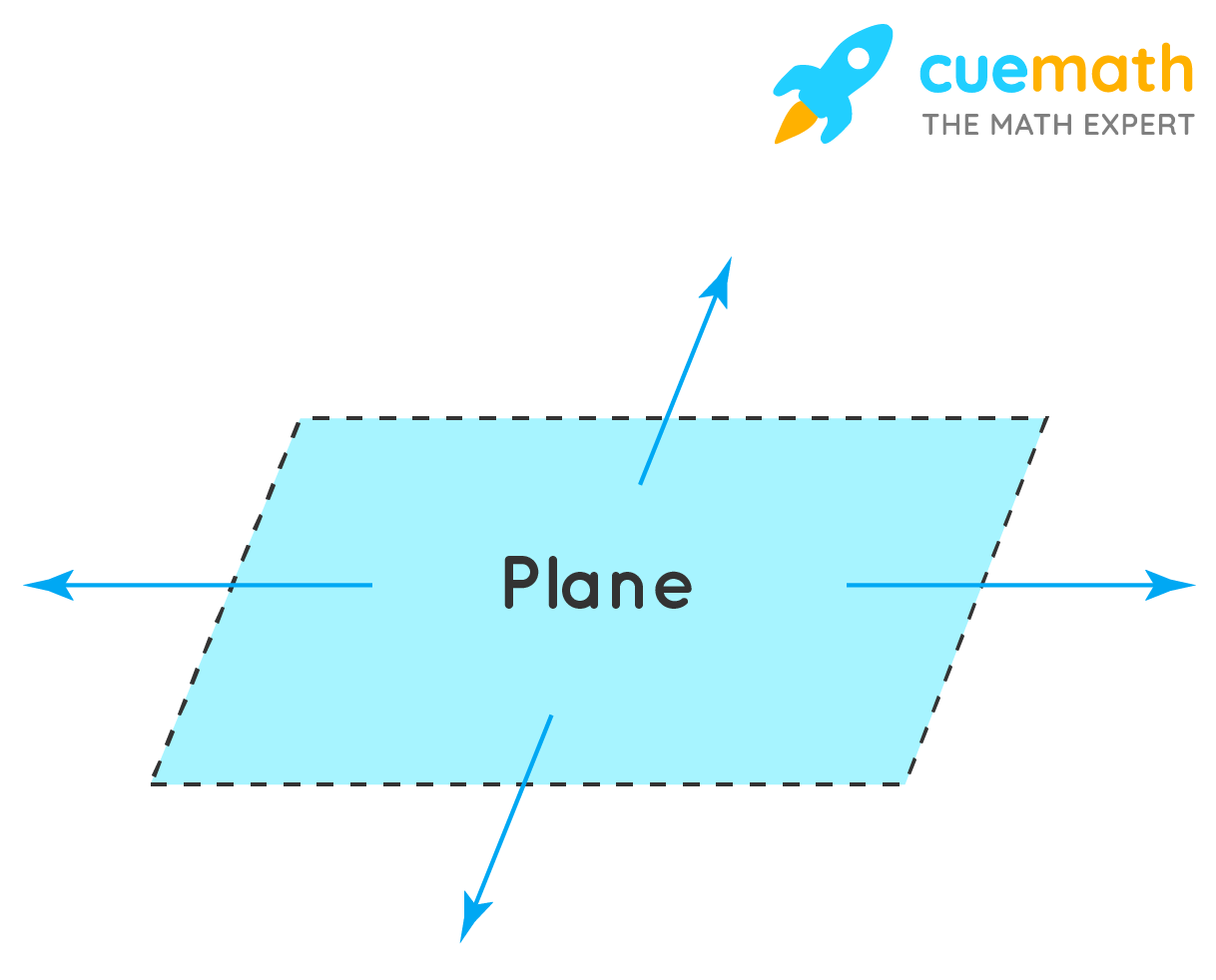
The figure shown above is a flat surface extending in all directions. So, it is a plane.
Properties of Planes
A plane in math has the following properties:
- If there are two distinct planes, then they are either parallel to each other or intersecting in a line.
- A line is either parallel to a plane, intersects the plane at a single point, or exists in the plane.
- If there are two distinct lines, which are perpendicular to the same plane, then they must be parallel to each other.
- If two different planes are perpendicular to the same line, they must be parallel.
How do you Make a Plane in Math?
In math, a plane can be formed by a line, a point, or a three-dimensional space. All the faces of a cuboid are planes. There is an infinite number of plane surfaces in a three-dimensional space.
Point
A point is defined as a specific or precise location on a piece of paper or a flat surface, represented by a dot. It has no width. A point has zero dimensions.
Line
A line is a combination of infinite points together. It extends in both directions. It has one dimension. The planes are difficult to draw because you have to draw the edges. But it is important to understand that the plane does not actually have edges, and it extends infinitely in all directions. The plane has two dimensions - length and width. However, since the plane is infinitely huge, its length and width cannot be estimated. To represent the idea of a plane, we can use a four-sided figure as shown below:
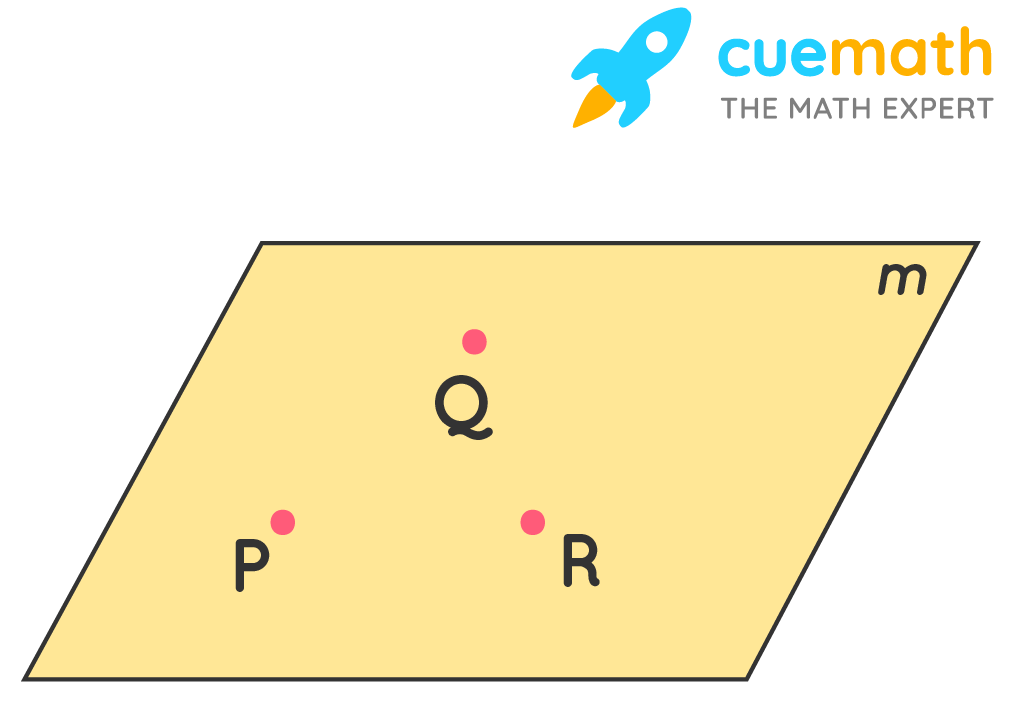
Therefore, we can call this figure plane QPR.
Identify Plane in a Three-Dimensional Space
In three-dimensional space, planes are all the flat surfaces on any one side of it. For example in the cuboid given below, all six faces of cuboid, those are, AEFB, BFGC, CGHD, DHEA, EHGF, and ADCB are planes. They all have only two dimensions - length and breadth.

Parallel Planes
Parallel planes are planes that never intersect. The below figure shows two planes, P and Q, that do not intersect each other. So, they are parallel planes. There are several examples of parallel planes, such as the opposite walls of the room and the floor.

Intersecting Planes
Intersecting planes are planes that are not parallel and they always intersect along a line. Two planes cannot intersect in more than one line. The below figure shows the two planes, P and Q, intersect in a single line XY. Therefore, the XY line is the common line between the P and Q planes. The two connecting walls are a real-life example of intersecting planes.
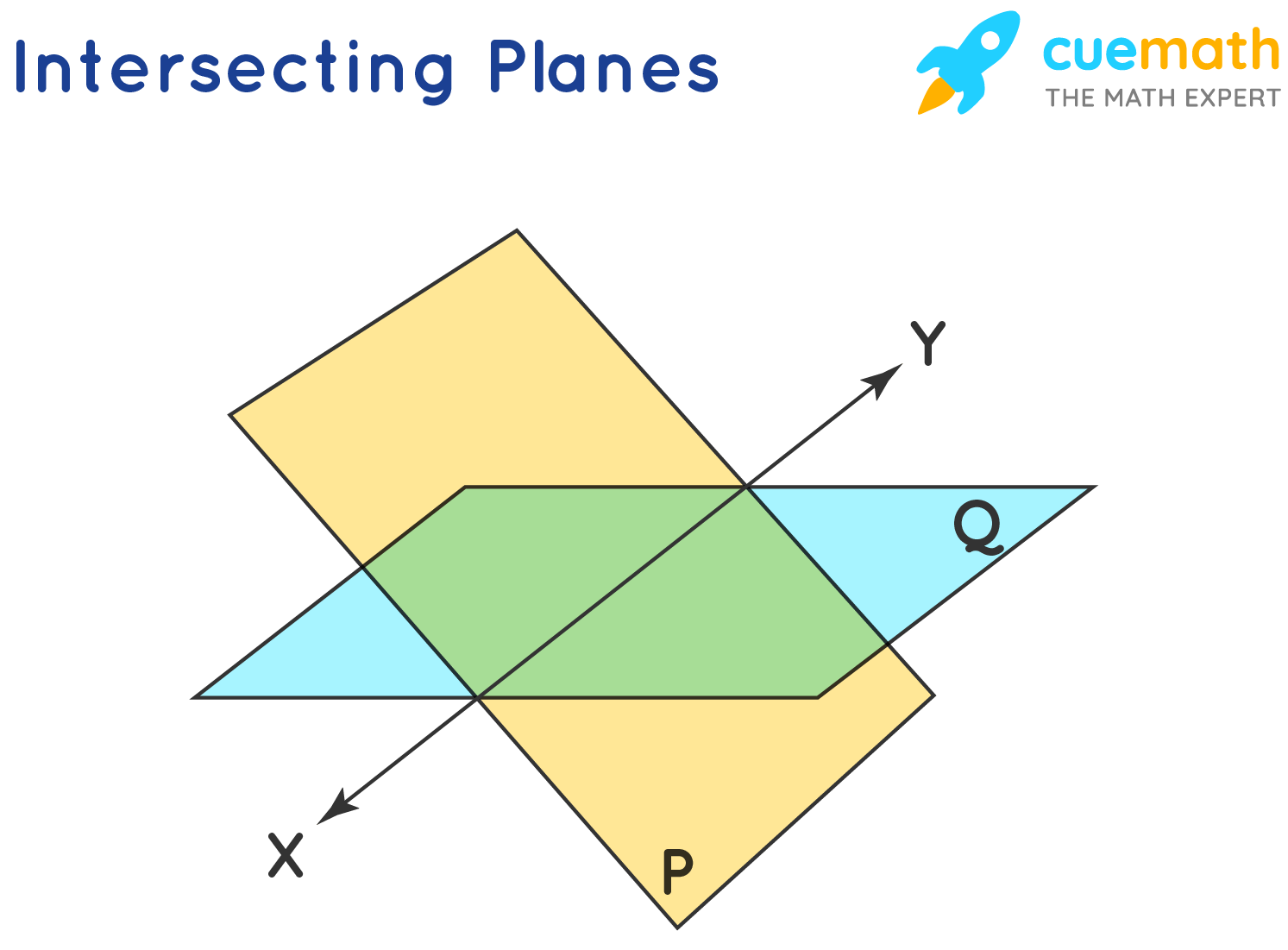
Naming of Planes in Geometry
Planes in geometry are usually referred to as a single capital (capital) letter in italics, for example, in the diagram below, the plane could be named UVW or plane P.

Important Notes
- Any three non-collinear points lie on one and only one plane.
- Two planes always intersect along a line, unless they are parallel.
- A plane is named by three points in that plane that are not on the same line.
Related Articles on Plane Definition
Check out these interesting articles on Plane. Click to know more!
Solved Examples on Plane
-
Example 1: Sophie, a teacher, is asking her students. Are the points P, E, R, H coplanar?

Solution:
According to the definition of coplanarity, points lying in the same plane are coplanar. Points P, E, R, and H lie in the same plane. So they are coplanar. ∴ Yes, points P, E, R, and H are coplanar.
-
Example 2: Anna was asked to give other names for plane P. Can you help her?

Solution:
We can name the plane by its vertices. So, in the given diagram, the plane could be named plane HDF, plane HGF, and plane HGD.

FAQs on Plane
How do you Define a Plane?
A plane is a flat two-dimensional surface. There is an infinite number of points and lines that lie on the plane. It can be extended up to infinity with all the directions. There are two dimensions of a plane- length and width.
What are the Examples of Plane Surfaces?
The surfaces which are flat are known as plane surfaces. Examples of plane surfaces are the surface of a room, the surface of a table, and the surface of a book, etc.
Is Diamond a Plane Shape?
A diamond is a 2-dimensional flat figure that has four closed and straight sides. Yes, it is a plane shape as it has two dimensions- length and width.
How Many Points do you Need for a Plane?
Any three noncollinear points make up a plane.
What is the Angle Between Two Intersecting Planes?
The angle between two intersecting planes is called the Dihedral angle.
How many Dimensions does a Plane have?
Planes are two-dimensional, but they can exist in three-dimensional space.
Is a Plane a Curved Surface?
A plane has two dimensions: length and width. All planes are flat surfaces. If it is not a flat surface, it is known as a curved surface.
visual curriculum