Linear Equations
A linear equation is an equation in which the highest power of the variable is always 1. It is also known as a one-degree equation. The standard form of a linear equation in one variable is of the form Ax + B = 0. Here, x is a variable, A is a coefficient and B is constant. The standard form of a linear equation in two variables is of the form Ax + By = C. Here, x and y are variables, A and B are coefficients and C is a constant.
What is a Linear Equation?
An equation that has the highest degree of 1 is known as a linear equation. This means that no variable in a linear equation has a variable whose exponent is more than 1. The graph of a linear equation always forms a straight line.
Linear Equation Definition: A linear equation is an algebraic equation where each term has an exponent of 1 and when this equation is graphed, it always results in a straight line. This is the reason why it is named as a 'linear' equation.
There are linear equations in one variable and linear equations in two variables. Let us learn how to identify linear equations and non-linear equations with the help of the following examples.
| Equations | Linear or Non-Linear |
|---|---|
| y = 8x - 9 | Linear |
| y = x2 - 7 | Non-Linear, the power of the variable x is 2 |
| √y + x = 6 | Non-Linear, the power of the variable y is 1/2 |
| y + 3x - 1 = 0 | Linear |
| y2 - x = 9 | Non-Linear, the power of the variable y is 2 |
Linear Equation Formula
The linear equation formula is the way of expressing a linear equation. This can be done in different ways. For example, a linear equation can be expressed in the standard form, the slope-intercept form, or the point-slope form. Now, if we take the standard form of a linear equation, let us learn the way in which it is expressed. We can see that it varies from case to case based on the number of variables and it should be remembered that the highest (and the only) degree of all variables in the equation should be 1.
- Slope intercept form of a linear equation is y = mx + c (where m = slope and c = y-intercept)
- Point slope form of a linear equation is y - y1 = m(x - x1) (where m = slope and (x1, y1) is a point on the line)
Note: The slope of a linear equation is the amount by which the line is rising or falling. It is calculated by the formula rise/run. i.e., if (x1, y1) and (x2, y2) are any two points on a line then its slope is calculated using the formula (y2 - y1)/(x2 - x1).
Linear Equations in Standard Form
The standard form or the general form of linear equations in one variable is written as, Ax + B = 0; where A and B are real numbers, and x is the single variable. The standard form of linear equations in two variables is expressed as, Ax + By = C; where A, B and C are any real numbers, and x and y are the variables.
Linear Equation Graph
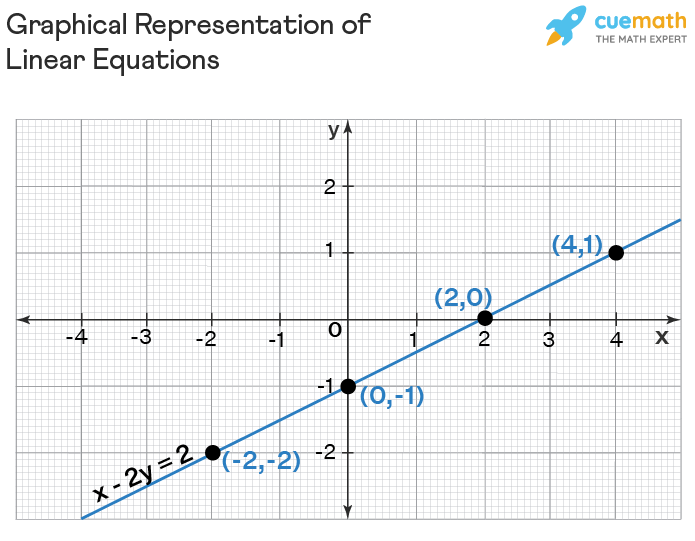
The graph of a linear equation in one variable x forms a vertical line that is parallel to the y-axis and vice-versa, whereas, the graph of a linear equation in two variables x and y forms a straight line. Let us graph a linear equation in two variables with the help of the following example.
Example: Plot a graph for a linear equation in two variables, x - 2y = 2.
Let us plot the linear equation graph using the following steps.
- Step 1: The given linear equation is x - 2y = 2.
- Step 2: Convert the equation in the form of y = mx + b. This will give: y = x/2 - 1.
- Step 3: Now, we can replace the value of x for different numbers and get the resulting value of y to create the coordinates.
- Step 4: When we put x = 0 in the equation, we get y = 0/2 - 1, i.e. y = -1. Similarly, if we substitute the value of x as 2 in the equation, y = x/2 - 1, we get y = 0.
- Step 5: If we substitute the value of x as 4, we get y = 1. The value of x = -2 gives the value of y = -2. Now, these pairs of values of (x, y) satisfy the given linear equation y = x/2 - 1. Therefore, we list the coordinates as shown in the following table.
| x | 0 | 2 | 4 | -2 |
|---|---|---|---|---|
| y | -1 | 0 | 1 | -2 |
- Step 6: Finally, we plot these points (4,1), (2,0), (0,-1) and (-2, -2) on a graph and join the points to get a straight line. This is how a linear equation is represented on a graph.
Linear Equations in One Variable
A linear equation in one variable is an equation in which there is only one variable present. It is of the form Ax + B = 0, where A and B are any two real numbers and x is an unknown variable that has only one solution. It is the easiest way to represent a mathematical statement. This equation has a degree that is always equal to 1. A linear equation in one variable can be solved very easily. The variables are separated and brought to one side of the equation and the constants are combined and brought to the other side of the equation, to get the value of the unknown variable.
Example: Solve the linear equation in one variable: 3x + 6 = 18.
In order to solve the given equation, we bring the numbers on the right-hand side of the equation and we keep the variable on the left-hand side. This means, 3x = 18 - 6. Then, as we solve for x, we get, 3x = 12. Finally, the value of x = 12/3 = 4.
☛Also check:
Linear Equations in Two Variables
A linear equation in two variables is of the form Ax + By + C = 0, in which A, B, C are real numbers and x and y are the two variables, each with a degree of 1. If we consider two such linear equations, they are called simultaneous linear equations. For example, 6x + 2y + 9 = 0 is a linear equation in two variables. There are various ways of solving linear equations in two variables like the graphical method, the substitution method, the cross multiplication method, the elimination method, and the determinant method.
☛Also check: Linear Equations In Two Variables Worksheets
How to Solve Linear Equations?
An equation is like a weighing balance with equal weights on both sides. If we add or subtract the same number from both sides of an equation, it still holds true. Similarly, if we multiply or divide the same number on both sides of an equation, it is correct. We bring the variables to one side of the equation and the constant to the other side and then find the value of the unknown variable. This is the way to solve a linear equation with one variable. Let us understand this with the help of an example.
Example: Solve the equation, 3x - 2 = 4.
We perform mathematical operations on the Left-hand side (LHS) and the right-hand side (RHS) so that the balance is not disturbed. So, let us add 2 on both sides to reduce the LHS to 3x. This will not disturb the balance. The new LHS is 3x - 2 + 2 = 3x and the new RHS is 4 + 2 = 6. Now, let us divide both sides by 3 to reduce the LHS to x. Thus, we have x = 2. This is one of the ways of solving linear equations in one variable.
Tips on Linear Equations:
- The value of the variable that makes a linear equation true is called the solution or root of the linear equation.
- The solution of a linear equation is unaffected if the same number is added, subtracted, multiplied, or divided into both sides of the equation.
- The graph of a linear equation in one or two variables always forms a straight line.
☛ Related Articles:
FAQs on Linear Equation
What is a Linear Equation? Explain with an Example.
A linear equation is an equation in which the highest power of the variable is always 1. It is also known as a one-degree equation. When this equation is graphed, it always results in a straight line. This is the reason why it is termed as a 'linear equation'. There are linear equations in one variable, in two variables, in three variables, and so on. A few examples of linear equations are 5x + 6 = 1, 42x + 32y = 60, 7x = 84, etc.
What is the Formula for a Linear Equation?
The formula for a linear equation is the way in which a linear equation is expressed. It can be expressed in the standard form, the slope-intercept form or the point-slope form. Using the slope-intercept form, the linear equation can be found using y = mx + c and using the point-slope form, it can be found using y - y1 = m(x-x1), where m is the slope, c is the y-intercept, and (x1, y1) is a point on the line.
Why is a Linear Equation Called Linear?
A linear equation is called linear because when we try to plot the graph of the given linear function, it results in a straight line.
How do you Solve Linear Equations?
We can solve a linear equation in one variable by moving the variables to one side of the equation, and the numeric part on the other side. For example, x - 1 = 5 - 2x can be solved by moving the numeric parts on the right-hand side of the equation, while keeping the variables on the left side. Hence, we get x + 2x = 5 + 1. Thus, 3x = 6. This gives x = 2.
Can Linear Equations have Fractions?
Yes, linear equations can have fractions only as long as the denominator in the fractional part is a constant value. The variables cannot be a part of the denominator of any fraction in a linear equation.
What are Linear Equations in One Variable?
A linear equation in one variable is an equation in which there is only one variable present. It is of the form Ax + B = 0, where A and B are any two real numbers and x is an unknown variable that has only one solution. For example, 9x + 78 = 18 is a linear equation in one variable.
How do You Convert a Linear Equation to Standard Form?
To convert a linear equation to standard form, you need to move all the variables to one side of the equation and the constants to the other side, and then rearrange the terms so that the variables are on the left side and the constant is on the right side.
What are Linear Equations in two Variables?
A linear equation in two variables is of the form Ax + By + C = 0, in which A and B are the coefficients, C is a constant term, and x and y are the two variables, each with a degree of 1. For example, 7x + 9y + 4 = 0 is a linear equation in two variables. If we consider two such linear equations, they are called simultaneous linear equations.
How are Quadratic Equations Different from Linear Equations?
Linear equations do not have any exponent other than 1 in any term. The general form of a linear equation is expressed as Ax + By + C = 0, where A, B, and C are any real numbers and x and y are the variables. Whereas, quadratic equations have at least one term containing a variable that is raised to the second power. The general form of a quadratic equation is expressed as ax2 + bx + c = 0. Another difference between the two types of equations is that a linear equation forms a straight line whereas a quadratic equation forms a parabola on the graph.
How to Graph Linear Equations?
When we graph linear equations, it forms a straight line. In order to graph an equation of the form, Ax + By = C, we get two solutions that are corresponding to the x-intercepts and the y-intercepts. We convert the equation to the form, y = mx + b. Then, we replace the value of x with different numbers and get the value of y which creates a set of (x,y) coordinates. These coordinates can be plotted on the graph and then joined by a line.
How to Solve Linear Equations with Fractions?
Linear equations with fractions are solved in the same way as we solve the usual equations. We need to bring the variable on one side and the constants on the other side and solve for the variable. For example, let us solve the equation (2a/3) - 10 = 12.
- Step 1: Here, we will bring the constants on the right-hand side, i.e., (2a/3) = 12 + 10.
- Step 2: Now, we have (2a/3) = 22. This can be further written as, 2a = 22 × 3.
- Step 3: Therefore, the value of a = 66/2 = 33.