Rise Over Run Formula

The rise over run formula is another way of saying the "slope formula" for a straight line joining any two points. The difference between the y-coordinates of the two points is called the rise. The difference between the x-coordinates of the same two points is called the run. The slope can be calculated by dividing the rise by run. Let us explore the rise over run formula (or slope formula) below.

What is Rise Over Run Formula?

The rise over run formula is referred to as the slope formula where the fraction consists of a rise whether the line is going up or down divided by the run i.e. either the line is going left or right. The slope of the line determines the direction of the line and determines how steep the line is. The image below explains it. 

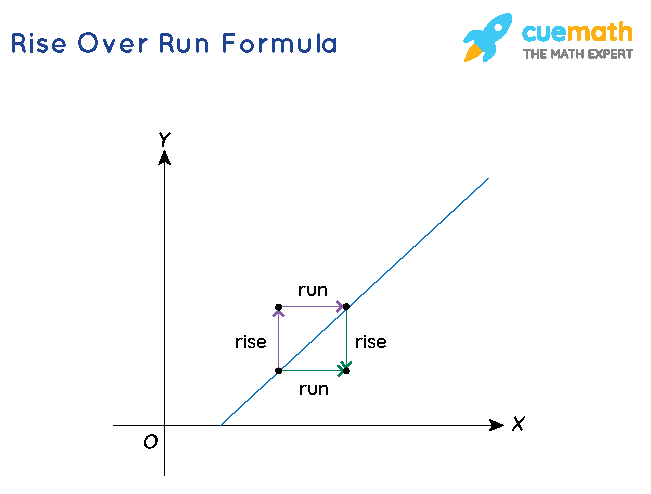
Rise over Run Formula

Consider a line joining two points A(\((x)_{1}\) , \((y)_{1}\)) and B(\((x)_{2}\) , \((y)_{2}\)). The slope of this line is the ratio of the difference in y coordinates and the difference in x coordinates. The same applies to the rise over run formula as well and the formula is:

Rise over run formula (or) slope (m) = \( \dfrac{y_2 - y_1}{x_2 - x_1} \) = \( \dfrac{\Delta y}{\Delta x} \)

Here,

• Rise = difference between the y-coordinates of points A and B = \((y)_{2}\) - \((y)_{1}\) = Δy
• Run = difference between the x-coordinates of points A and B = \((x)_{2}\) - \((x)_{1}\) = Δx

Rules of Rise Over Run Formula 

The rise over run formula helps in determining the slope of a straight line that can be negative, positive, or zero. Listed below are a few things to keep in mind:

• If the straight line is going from left to right and upwards, the line is a rising line with the slope being positive
• If the straight line is going from left to right and downwards, the line is falling line with the slope being negative
• If the straight line is horizontal, the slope will be zero
• If the straight line is vertical, the slope is undefined

Examples Using Rise Over Run Formula 

Example 1: Find the slope of the line joining points A(0, 4) and B(1, 7) using the rise over run formula. Also, write the equation of this line in standard form.

Solution.

Slope (m) = \( \dfrac{y_2 - y_1}{x_2 - x_1} \) = \( \dfrac{7 - 4}{1 - 0} \) = 3

Using the slope-intercept form, equation of this line can be written as 

y = mx + c

y = 3x + c 

Point (0, 4) passes through the line, so substituting x = 0 and y = 4 in the above line equation we get,

4 = 3(0) + c

c = 4

Therefore, the line equation is y = 3x + 4

Converting the line into standard form

y = 3x + 4

Subtracting y on both sides we get, 

3x - y + 4 = 0

Subtracting 4 on both sides we get,

3x - y = -4 (Standard Form)

Therefore, the slope of the line joining A and B is 3. The standard form of this line equation is 3x - y = -4

Example 2: A square of side = 4 units has one of its corner points A(1, 1). Given that the square is in the first quadrant and its sides are parallel with the x-axis and the y-axis. Find the slopes of both diagonals of this square.  

Solution.

This is the only possible square for the given conditions.

Since line joining A and B is parallel to the y-axis, this implies that the x-coordinates of both A and B are the same. 

A = (1, 1) B = (1, y)

The distance between A and B is 4 units.

Using the distance formula \(AB = 4 = \sqrt{(1 -1)^2 + (y-1)^2}\) gives y = 5.

Therefore coordinates of B are (1, 5).

Similarly, coordinates of C are (5, 5) and coordinates of D are (5, 1).

Let \((m)_{1}\) and \((m)_{2}\) be the slopes of both the diagonals of the square. Let us find them using the rise over run formula.

\((m)_{1}\) = \( \dfrac{5 - 1}{5 - 1} \) = 1 (for the diagonal AC) 

\((m)_{2}\) = \( \dfrac{5 - 1}{1 - 5} \) = -4 (for the diagonal BD)

Therefore, the slopes of both the diagonals are \((m)_{1}\) = 1 and \((m)_{2}\) = -4.

Example 3: Find the slope of the line joining points A(1, 5) and B(2, 8) using the rise over run formula.

Solution:

Using the rise over run formula, 

Slope (m) = \( \dfrac{y_2 - y_1}{x_2 - x_1} \) = \( \dfrac{8 - 5}{2 - 1} \) = 3 

Therefore, the slope is 3.