Point Slope Form
The point slope form is used to find the equation of the straight line which is inclined at a given angle to the x-axis and passes through a given point. The equation of a line is an equation that is satisfied by each and every point on the line. This means that a linear equation in two variables represents a line. The equation of a line can be found through various methods depending on the available information. Some of the methods are:
- Point slope form
- Slope-intercept form
- Intercept form
- Two-point form
Point slope formula is used only when we know the slope of the line and a point on the line. Let us learn about the point slope form and how to derive the formula to represent point slope form in detail in the following section.
| 1. | What is Point Slope Form? |
| 2. | Point Slope Formula |
| 3. | Derivation of Point Slope Formula |
| 4. | Point Slope Formula Examples |
| 5. | How to Solve Point Slope Form? |
| 6. | FAQs on Point Slope Form |
What is Point Slope Form?
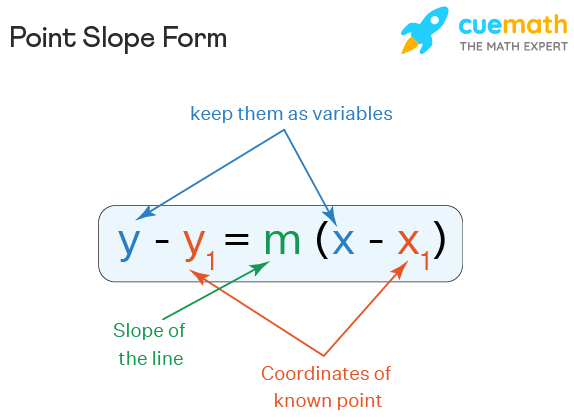
Point slope form is used to represent a straight line using its slope and a point on the line. That means, the equation of a line whose slope is 'm' and which passes through a point (x\(_1\), y\(_1\)) is found using the point slope form. Different forms can be used to express the equation of a straight line. One of them is point slope form. The equation of the point slope form is:
y - y\(_1\) = m(x - x\(_1\))
where, (x, y) is a random point on the line and m is the slope of the line.
Point Slope Formula
The point slope form formula is used to find the equation of a line. The equation of a line with a given slope and with a given point is found using the point slope form. This formula is used only when we know the slope of the line and a point on the line. We have some other formulas as well to find the equation of a line such as slope-intercept form, intercept form, etc. Here is the point slope formula,
Point Slope Formula in Math:
y − y\(_1\) = m (x − x\(_1\))
where,
- (x, y) is a random point on the line(which should be kept as variables while applying the formula).
- (x\(_1\), y\(_1\)) is a fixed point on the line.
- m is the slope of the line.
Derivation of Point Slope Formula
Let us see how to find the point slope form (i.e. the proof of the formula of the point slope form). We will derive this formula using the equation for the slope of a line. Let us consider a line whose slope is 'm'. Let us assume that (x\(_1\), y\(_1\)) is a known point on the line. Let (x, y) be any other random point on the line whose coordinates are not known.
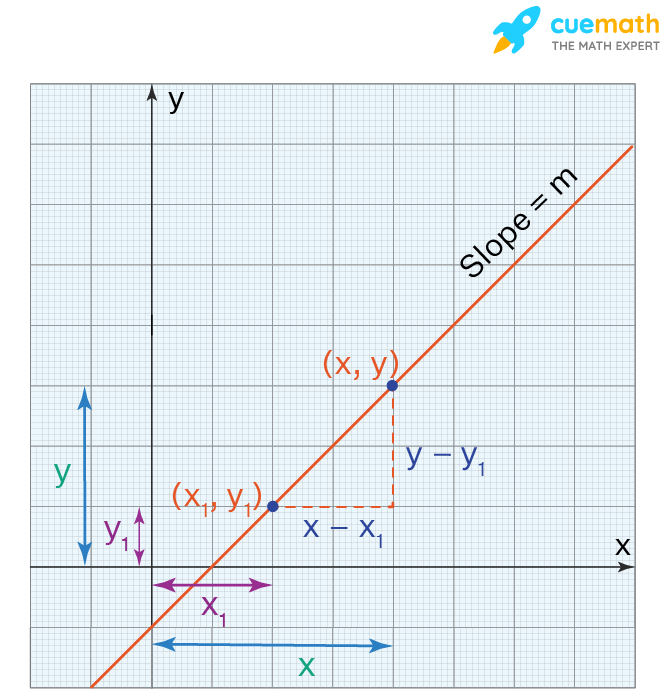
We know that the equation for the slope of a line is:
Slope = (Difference in y-coordinates)/(Difference in x-coordinates)
m = (y - y\(_1\))/(x - x\(_1\))
Multiplying both sides by (x - x\(_1\)),
m(x - x\(_1\)) = y - y\(_1\)
This can be written as,
y - y\(_1\) = m(x - x\(_1\))
Hence the point slope formula is proved.
Point Slope Formula Examples
Some examples of the point slope form formula are shown here.
- The equation of a line with slope (-1) and a point (1, 2) is found using: y - 2 = (-1)(x - 1).
- The equation of a line with slope (3/2) and a point (-1/2, 2/3) is found using: y - (2/3) = (3/2) (x - (-1/2)).
- The equation of a line with slope (0) and a point (3, -2) is found using: y - (-2) = 0(x - 3).
In each of these cases, we can simplify the equation further and get it to the form: y = mx + b.
Important notes on Point Slope Form:
- The equation of the point slope form of a line whose slope is 'm' and that passes through a point (x\(_1\), y\(_1\)) is y - y\(_1\) = m(x - x\(_1\)).
- The equation of a horizontal line passing through (a, b) is of the form y = b.
- The equation of a vertical line passing through (a, b) is of the form x = a.
This is an exceptional case where the point slope form cannot be used.
How to Solve Point Slope Form?
To solve point slope form for a given straight line for finding the equation of the given line, we can follow the steps given below,
- Step 1: Note down the slope, 'm' of the straight line, and the coordinates(x\(_1\), y\(_1\)) of the given point that lies on the line.
- Step 2: Substitute the given values in the point slope formula: y - y\(_1\) = m(x - x\(_1\)).
- Step 3: Simplify to obtain the equation of the line in standard form.
☛ Also Check: You can try this point slope form calculator to verify the result obtained for the equation of a line segment- Point-Slope Form Calculator
Let us see an example to understand the application of above steps on point slope form.
Example: Find the equation of a line that passes through a point (2, -3) and whose slope is (-1/2).
Solution:
The point on the given line is: (x\(_1\), y\(_1\)) = (2, -3)
The slope of the line is: m = (-1/2)
The equation of the line is found using the point slope form:
y − y\(_1\) = m(x − x\(_1\))
y − (−3) = (−1/2)(x − 2)
y + 3 = (−1/2)x + 1
Subtracting 3 from both sides,
y = (−1/2)x − 2
Thus, the equation of the required line is, y = (−1/2)x − 2
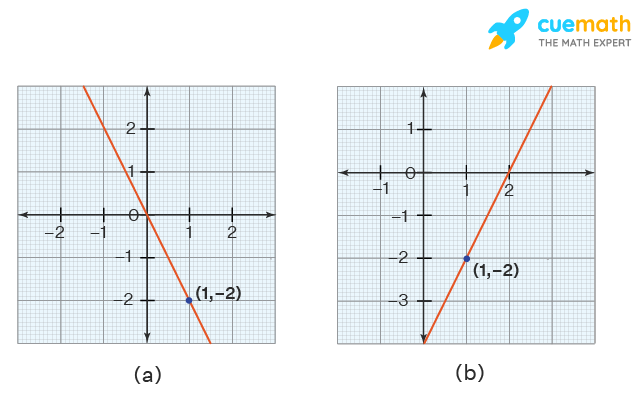
Thinking out of the box:
Which of the following graphs may represent the equation y + 2 = −2(x − 1)?
☛ Articles Related to Point Slope Form:
Check out few more interesting articles which consist of additional conceptual ideas revolving around point slope form.
Let us understand point slope form better using solved examples.
Examples on Point Slope Form
-
Example 1: Find the equation of the following line.

Solution:
We know that the slope of a vertical line is undefined, i.e. m = ∞.
Thus, the equation of the given line can't be found using the point slope form.
We will use the form listed under the "important notes" section of this page which is:
The equation of the vertical line passing through (a, b) is of the form x = a.
Let us take any point on the line:
(a, b) = (4, 1)
∴The equation of the line using the above form is, x = 4.
-
Example 2: Find the equation of a horizontal line that passes through a point (3, 2).
Solution:
Method 1:
We know that the slope of a horizontal line is m = 0.
The line passes through the point (x\(_1\), y\(_1\)) = (3, 2)
The equation of the line using the point slope form is:
y − y\(_1\) = m (x − x\(_1\))
y − 2 = 0(x − 3)
y − 2 = 0
y = 2
Method 2:
From the formulas listed under the "important notes" section of this page, we know that:
The equation of a horizontal line passing through (a, b) is of the form y = b.
A point on the given line is,
(a, b) = (3, 2)
Thus, the equation of the required horizontal line is:
y = 2
From both the methods, the equation of the given line is:
∴ y = 2 -
Example 3: Find the equation of a line that passes through two points (1, 3) and (-2, 4) using the point slope form and express the answer in the standard form.
Solution:
The given two points are:
(x\(_1\), y\(_1\)) = (1, 3)
(x\(_2\), y\(_2\)) = (−2, 4)
To use the point slope form, we first need to find the slope of the line.
The slope of the given line is found using:
m = [y\(_2\) − y\(_1\)]/[x\(_2\) − x\(_1\)] = (4 − 3)/(−2 −1) = −1/3Applying point slope formula, y - 3 = (-1/3)(x - 1)
To express this in the standard form, first, we multiply both sides by 3.
3y - 9 = -x + 1
⇒ 3y = -x + 10Adding x on both sides,
x + 3y = 10Thus, the equation of the given line in the standard form is:
∴ x + 3y = 10

FAQs on Point Slope Form
What is the Point Slope Form of a Straight Line in Geometry?
The point slope form of a straight line in geometry is used to represent the equation of a straight line using its slope 'm' and a point(x, y) that lies on the given line. The point slope form is given as, y − y\(_1\) = m(x − x\(_1\)).
How do you Find the Point Slope Form with a Point Slope?
The point slope formula is a formula that is used to find the equation of a line. This formula is used only when we know the slope of a line and a point on the line. The equation of a line whose slope is m and which passes through a point (x\(_1\), y\(_1\)) is found using the point slope formula. The equation of the point slope form is: y − y\(_1\) = m(x − x\(_1\)). Here (x, y) is a random point on the line.
How do you Change Point Slope Form into Slope-Intercept Form?
The point slope form is of the form: y − y\(_1\) = m(x − x\(_1\)). We will solve this equation for y which gives an equation of the form, y = mx + b. This is called the slope-intercept form.
What is the Point Slope Formula?
The point slope formula is one of the formulas that is used to find the equation of a line. The point slope formula says the equation of a line with slope 'm' and a point \((x_1, y_1)\) on it is, y − y\(_1\) = m (x − x\(_1\)).
How do you Write Point Slope Form of a Straight Line?
The point slope form of a straight line with slope 'm' and a point with coordinates (x\(_1\), y\(_1\)) is given as, y − y\(_1\) = m (x − x\(_1\)).
How to Derive the Point Slope Formula?
To derive the point slope formula, we consider a line of slope 'm' with a point \((x_1, y_1)\). If (x, y) is any general point on the line, then the slope of the line is, m = (y - y\(_1\))/(x - x\(_1\). From this, we can get the point slope formula y − y\(_1\) = m (x − x\(_1\)).
What are the Applications of Point Slope Formula?
The point slope formula is used to:
- find the equation of a line with the given slope and a point on it.
- graph the line just using the slope and one point on the line.
- find the slope of the line right away from the equation of the line.
How to Derive the Slope-Intercept Formula Using Point Slope Formula?
The point slope formula is of the form y − y\(_1\) = m (x − x\(_1\)) whereas the slope-intercept formula is of the form y = mx + b, where 'm' is the slope, 'b' is the y-intercept, and (x\(_1\), y\(_1\)) is a point on the line. To derive the slope-intercept formula from point slope formula, we will just have to solve it for y. Here is an example.
Point slope form of a line: y - 3 = 4 (x - 1)
y - 3 = 4x - 4
Adding 3 on both sides,
⇒ slope-intercept form: y = 4x - 1
What is an Example of Point Slope Form?
Some examples of point slope form of a line are as given below,
- The equation of a line with slope (1) and a point (1, 3) is found using: y - 3 = (1)(x - 1).
- The equation of a line with slope (1/2) and a point (-1/2, 2/3) is found using: y - (2/3) = (1/2) (x - (-1/2)).
How do you Find the Point Slope Form From a Graph?
To find the point slope form of a line, we just find the slope and a point on the line. A point on the line can be easily found by looking at its graph. The slope of a line is found by first finding any two points on the line from its graph and then applying the formula: Slope = (Difference in y-coordinates)/(Difference in x-coordinates).
visual curriculum