Undefined Slope
The undefined slope is the slope of a vertical line. The x-coordinates do not change, no matter what y coordinates are. The vertical lines rise straight up or fall straight down, whereas they don't run left or right. The slope is the ratio of the change in y coordinates to the change in x coordinates. Since there is no change in x coordinates, for a vertical line, the denominator is zero which makes the slope undefined, or the slope cannot exist.
Let us understand the undefined slope and undefined slope graph with a few examples.
| 1. | What is Undefined Slope? |
| 2. | Undefined Slope Equation |
| 3. | Undefined Slope Graph |
| 4. | How To Find The Undefined Slope? |
| 5. | FAQs on Undefined Slope |
What is Undefined Slope?
The slope of a straight line is the tangent of its inclination to the x-axis and is denoted by ‘m’ i.e. if the inclination of a line is θ, its slope m = tan θ. The straight line that is either parallel to the y-axis or that coincides with the y-axis is the vertical line. For vertical lines, the angle of inclination θ = 90°, then slope m = tan 90° = undefined.
Another way to determine is slope = rise/run. For vertical lines, there is no run at all, thus making the denominator zero. We get an undefined slope. In other words, slope = \(\dfrac{y_2-y_1}{x_2-x_1}\) = Change in y coordinates/ change in x-coordinates. When the x values are the same for the vertical lines, there could be no change in the value of x.
Undefined Slope Equation
The slope of the y-axis or the slope of any straight line that is parallel to the y-axis is undefined since tan 90° is undefined. The equation of a straight line with an undefined slope is given as x = a, where a is any real number and it is a constant. It denotes that every point on the line has the x coordinates as 'a' throughout, regardless of the points picked. In particular, 'a' denotes the x-intercept, i.e., where the line crosses the x-axis.
Undefined Slope Examples
Here are some equations of an undefined slope.
- The equation for the y-axis is x = 0.
- The equation of the line passing through the points (-5,2) and (-5, -3) is x = -5
- The equation of the line passing through (3, -4) with an undefined slope is x = 3.
A few real-life examples that could be cited having undefined slope are the elevators that move only up and down, a mountain cliff that is vertical up to a finite distance that a mountaineer finds difficulty in climbing at, the skyscrapers, the lamp posts, or the flag posts, the sides of the doors or windows, the legs of the chair, the rocket at the time of launch and so on wherever we get to see vertical lines possible.
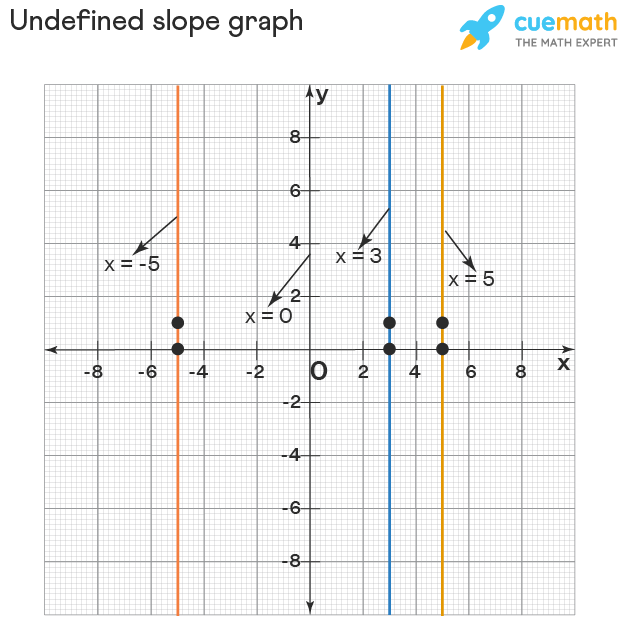
Undefined Slope Graph
Any vertical line is parallel to the y-axis. A line parallel to the y-axis does not intercept the y-axis and hence, we cannot get any y-intercept of such a line. Thus, any line parallel to the y-axis cannot be expressed in the intercept form. The following is the graphical representation of the undefined slope of the lines x = -5, x = 0 , x = 3 and x = 5.
How To Find The Undefined Slope?
We know that a vertical line is a perpendicular line to the x-axis that has an undefined slope. If we have a pair of coordinates, (x1, y1) and (x1,y2) through which a line passes, it is evident that the x-coordinates are the same. They are the points on the same vertical line. Thus the slope of such a line will be undefined.
Differences between zero slope and undefined slope
The horizontal lines that are parallel to the x-axis have a Zero Slope, whereas the vertical lines that are parallel to the y-axis have an undefined slope. The graph of a line with zero slope is y = b, whereas that with an undefined slope is x = a, where 'b' and 'a' are y and x-intercepts respectively.
Important Notes on the undefined slope
- An undefined slope is that of any line that is parallel to the y-axis, i.e. a vertical line.
- An undefined slope graph is x =a, where 'a' is the value of the x-coordinate that remains constant, throughout the line.
- The line with an undefined slope cannot be represented in the slope-intercept form as there is no y-intercept at all.
☛ Related Topics:
Examples of Undefined Slope
-
Example 1: Find the equation of the line that passes through (1,2), with an undefined slope.
Solution:
Any line that has an undefined slope is a vertical line, that has no y-intercept.
Therefore the equation of a line with an undefined slope is x = a, where a = x-intercept.
Here a = 1. Thus the required equation is x = 1.
Answer: The equation of a line with an undefined slope passing through (1,2) is x = 1
-
Example 2: A line has an undefined slope passing through the point (-2, 5). Explain why this line cannot be represented in slope-intercept form.
Solution:
y = mx + c is the equation of the straight line in the slope-intercept form. m = slope = undefined
Thus this is a vertical line. The equation of the vertical line is x = -2.
y = c, c is the value where the line cuts the y-axis. The vertical line is parallel to the y-axis.
Hence there is no y-intercept. Thus the line x = -2 cannot be represented in slope-intercept form.
Answer: The equation of the vertical line is x = -2 is parallel to the y-axis and hence cannot be represented in slope-intercept form.
-
Example 3: Verify if the slope of the line that runs through the points (2, -5) and (2, -3) is an undefined slope?
Solution:
Slope = change in y coordinates/ change in x-coordinates
= -3-(-5)/2-2
= 2/0 = undefined. Hence verified.
Answer: Thus the slope of the line that runs through the points (2, -5) and (2, -3) is undefined.

FAQs on Undefined Slope
What is an Undefined Slope?
The undefined slope is the slope of any vertical line that goes up or down. There is no horizontal movement and hence the denominator is zero while calculating the slope. Thus the slope of the line is undefined.
What is the Equation of Undefined Slope?
The slope of a straight line is the trigonometric tangent of the angle θ that the line makes with the positive direction of the x-axis. The lines that are parallel to the y-axis, are perpendicular to the x-axis. Thus the inclined angle is 90° and tan 90° = undefined. The equation of undefined slope is that of a vertical line that is x = a, where a is the x-intercept or any constant.
How do You Calculate the Undefined Slope?
We calculate the rise over run and find that there is no run or no change in x coordinates. Thus we determine that the slope is undefined as the denominator becomes zero in the fraction.
How is the graph of an Undefined Slope?
The Undefined slope graph is a line parallel to the y-axis or perpendicular to the x-axis. Thus there is no y-intercept and there is no change in the x-coordinates. The x values of the points on this line remain the same.
What is an Undefined Slope Example?
An example for an undefined slope could be a line passing through the points (4, -5) and (4,8). The slope of a line passing through the points is given as \(\dfrac{y_2-y_1}{x_2-x_1}\). Thus we have \(\dfrac{8+5}{4-4}\)= 13/0 is undefined.
Do we Have an Undefined Slope when a Line is Parallel to the y-axis?
Yes, any line parallel to the y-axis has an undefined slope as the angle of inclination to the x-axis is 90°. Slope = tan 90° = undefined.
Is a zero Slope Undefined?
No. A zero slope is that of a horizontal line. A slope is undefined for a vertical line. Any line parallel to the y-axis has an undefined slope.
visual curriculum