First Derivative Test

The first derivative test is the simplest method of finding the local maximum and the minimum points of a function. The first derivative test works on the concept of approximation, which finds the local maxima and local minima by taking values from the left and from the right in the neighborhood of the critical points and substituting it in the expression of the first derivative.

Let us learn more about the first derivative test, steps for the test, uses, and examples of the first derivative test.

The first derivative test helps in finding the turning points, where the function output has a maximum value or a minimum value. For the first derivative test. we define a function f(x) on an open interval I. Let the function f(x) be continuous at a critical point c in interval I. Here we have the following conditions, to find the local maximum and minimum, by using the first derivative test.

• If f ′(x) changes sign from positive to negative as x increases through (c, f(c)) i.e., if f ′(x) > 0 at every point sufficiently close to and to the left of (c, f(c)) and f ′(x) < 0 at every point sufficiently close to and to the right of (c, f(c)) then c is a point of local maxima.
• If f ′(x) changes sign from negative to positive as x increases through (c, f(c)) i.e., if f ′(x) < 0 at every point sufficiently close to and to the left of (c, f(c)) and f ′(x) > 0 at every point sufficiently close to and to the right of (c, f(c)) then c is a point of local minima.
• If f ′(x) does not change significantly as x increases through (c, f(c)) then c is neither a point of local maxima nor a point of local minima. In fact, such a point is called a point of inflection.

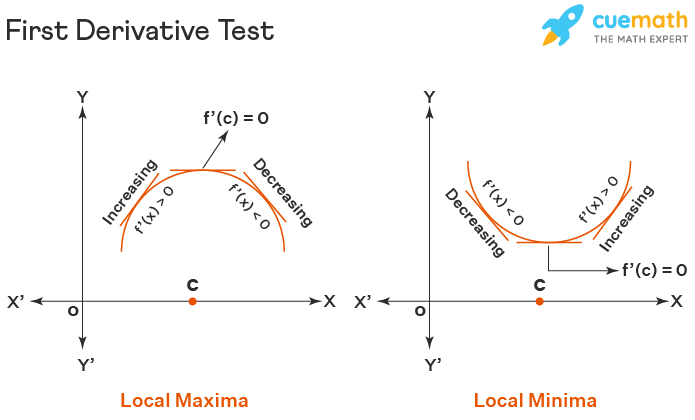
Local Maxima: Here in the first graph above, (c, f(c)) is a point of local maxima, since f'(x) > 0 towards its left, and f'(x) < 0 towards its right.

Local Minima: Here in the second graph above (c, f(c)) is a point of local minima, since f'(x) < 0 towards its left, and f'(x) > 0 towards its right.

The following steps are helpful to complete the first derivative test and finding the limiting points.

• For the given function f(x), find the first derivative f'(x).
• Find the limiting points by equalizing the first derivative expression to zero f'(x) = 0.
• Find one point each in the neighboring left side and the neighboring right side of the limiting point.
• Substitute these neighboring points in the first derivative functions.
• If the differentiation of the function is positive f'(x) > 0, for the neighboring point to the left, and it is negative f'(x) < 0, for the neighboring point to the right, then the limiting point is the local maxima.
• If the differentiation of the function is negative f'(x) < 0, for the neighboring point to the left, and it is positive f'(x)>0, for the neighboring point to the right, then the limiting point is the local minima.

The first derivative test is beneficial in a number of ways, which can be understood from the following applications.

• The first derivative test can be used to find the local maxima and local minima of a function, under certain constraints.
• The first derivative test is useful to find the optimal solution for the problem situation.
• For a parabolic equation the first derivative test helps in finding the turning point or the vertex of a parabola, and also gives the orientation of the parabola.
• The first derivative test helps in knowing the extreme points of the curves.
• The first derivative test helps us to know if the curve concaves up or concaves down.

Further, the first derivative test can be applied in the following real-life situations.

• The profit from a grove of orange trees is given by the algebraic expression P(x) = ax + bx²+ cx³ + d, where a, b are constants and x is the number of mango trees per acre. To find the number of mango trees per acre, which are required to maximize the profit we use this first derivative test.
• A ball thrown in the air from the top of a building of height 10m, travels along the path given by the formula h(x) = 60 + x - x²/60., where x is the horizontal distance and h(x) is the height of the ball. To find the maximum height the ball would reach, we use the first derivative test.
• A helicopter of the enemy is traveling along the path defined by the equation P(x) = x + 7, and a soldier placed at the point (1, 2) wants to hit the helicopter. Here to find the minimum distance at which the soldier can hit the helicopter, we can use the first derivative test.

☛Related Topics:

The following topics help for a better understanding of the first derivative test.

• Mean Value Theorem
• Rolle's Theorem
• Differential Equations Formula
• Application of Derivatives

What is First Derivative Test?

The first derivative test is the simplest method of finding the local maximum and the minimum points of a function. The first derivative test depends on the concept of approximation, to find the local maxima and local minima by taking the point to the left and to the right in the neighborhood of the critical points and substituting it in the expression of the first derivative.

How Do You Do the First Derivative Test?

The first derivative test can be performed through the following sequence of steps.

• Find the given function f(x), find the first derivative f'(x).
• Find the limiting points by equalizing the first derivative expression to zero.
• Find one point in each of the neighboring left side and the neighboring right side of the limiting point, and substitute in the first derivative function.
• If the derivative of the function is positive f(x) > 0, for the neighboring point to the left, and it is negative f(x) < 0, for the neighboring point to the right, then the limiting point is the local maxima.
• If the derivative of the function is negative f(x) < 0, for the neighboring point to the left, and it is positive f(x) > 0, for the neighboring point to the right, then the limiting point is the local minima.

What is the Difference Between First Derivative Test and Second Derivative Test?

The first derivative test and the second derivative test are both helpful to find the local maximum and minimum points. The first derivative test takes only the first derivative of the function, and takes a few points in the neighborhood of the turning points, to find if it is the maximum or the minimum point. The second derivative takes the first derivative and the second derivative of the given function. Here the limiting points obtained from the first derivative are checked through the second derivative to find the maximum and the minimum point.

Can the First Derivative Test Fail?

The first derivative test can fail if the limiting point is not the local maximum or the minimum of the given function. If the points to the left and the right of the limiting point have the same derivative values, then we cannot conclude about the point, and the first derivative test fails.

When Does the First Derivative Test Fail?

The first derivative test fails when the points to the left and the right of the limiting point have the same derivative values. In this case, we cannot define if the limiting point is the maxima or the minima and this limiting point is called the point of inflection.